The Convolution Exponential and Generalized Sylvester Flows
Paper and Code
Jun 02, 2020
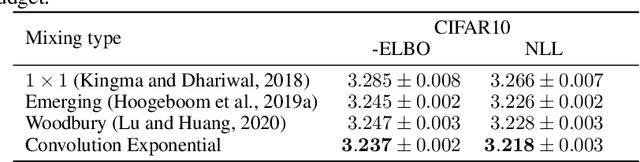

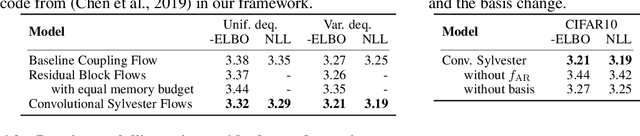
This paper introduces a new method to build linear flows, by taking the exponential of a linear transformation. This linear transformation does not need to be invertible itself, and the exponential has the following desirable properties: it is guaranteed to be invertible, its inverse is straightforward to compute and the log Jacobian determinant is equal to the trace of the linear transformation. An important insight is that the exponential can be computed implicitly, which allows the use of convolutional layers. Using this insight, we develop new invertible transformations named convolution exponentials and graph convolution exponentials, which retain the equivariance of their underlying transformations. In addition, we generalize Sylvester Flows and propose Convolutional Sylvester Flows which are based on the generalization and the convolution exponential as basis change. Empirically, we show that the convolution exponential outperforms other linear transformations in generative flows on CIFAR10 and the graph convolution exponential improves the performance of graph normalizing flows. In addition, we show that Convolutional Sylvester Flows improve performance over residual flows as a generative flow model measured in log-likelihood.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge