The Cross-environment Hyperparameter Setting Benchmark for Reinforcement Learning

This paper introduces a new empirical methodology, the Cross-environment Hyperparameter Setting Benchmark, that compares RL algorithms across environments using a single hyperparameter setting, encouraging algorithmic development which is insensitive to hyperparameters. We demonstrate that this benchmark is robust to statistical noise and obtains qualitatively similar results across repeated applications, even when using few samples. This robustness makes the benchmark computationally cheap to apply, allowing statistically sound insights at low cost. We demonstrate two example instantiations of the CHS, on a set of six small control environments (SC-CHS) and on the entire DM Control suite of 28 environments (DMC-CHS). Finally, to illustrate the applicability of the CHS to modern RL algorithms on challenging environments, we conduct a novel empirical study of an open question in the continuous control literature. We show, with high confidence, that there is no meaningful difference in performance between Ornstein-Uhlenbeck noise and uncorrelated Gaussian noise for exploration with the DDPG algorithm on the DMC-CHS.

Investigating the Interplay of Prioritized Replay and Generalization

Experience replay is ubiquitous in reinforcement learning, to reuse past data and improve sample efficiency. Though a variety of smart sampling schemes have been introduced to improve performance, uniform sampling by far remains the most common approach. One exception is Prioritized Experience Replay (PER), where sampling is done proportionally to TD errors, inspired by the success of prioritized sweeping in dynamic programming. The original work on PER showed improvements in Atari, but follow-up results are mixed. In this paper, we investigate several variations on PER, to attempt to understand where and when PER may be useful. Our findings in prediction tasks reveal that while PER can improve value propagation in tabular settings, behavior is significantly different when combined with neural networks. Certain mitigations -- like delaying target network updates to control generalization and using estimates of expected TD errors in PER to avoid chasing stochasticity -- can avoid large spikes in error with PER and neural networks, but nonetheless generally do not outperform uniform replay. In control tasks, none of the prioritized variants consistently outperform uniform replay.

When is Offline Policy Selection Sample Efficient for Reinforcement Learning?

Offline reinforcement learning algorithms often require careful hyperparameter tuning. Consequently, before deployment, we need to select amongst a set of candidate policies. As yet, however, there is little understanding about the fundamental limits of this offline policy selection (OPS) problem. In this work we aim to provide clarity on when sample efficient OPS is possible, primarily by connecting OPS to off-policy policy evaluation (OPE) and Bellman error (BE) estimation. We first show a hardness result, that in the worst case, OPS is just as hard as OPE, by proving a reduction of OPE to OPS. As a result, no OPS method can be more sample efficient than OPE in the worst case. We then propose a BE method for OPS, called Identifiable BE Selection (IBES), that has a straightforward method for selecting its own hyperparameters. We highlight that using IBES for OPS generally has more requirements than OPE methods, but if satisfied, can be more sample efficient. We conclude with an empirical study comparing OPE and IBES, and by showing the difficulty of OPS on an offline Atari benchmark dataset.

Empirical Design in Reinforcement Learning

Empirical design in reinforcement learning is no small task. Running good experiments requires attention to detail and at times significant computational resources. While compute resources available per dollar have continued to grow rapidly, so have the scale of typical experiments in reinforcement learning. It is now common to benchmark agents with millions of parameters against dozens of tasks, each using the equivalent of 30 days of experience. The scale of these experiments often conflict with the need for proper statistical evidence, especially when comparing algorithms. Recent studies have highlighted how popular algorithms are sensitive to hyper-parameter settings and implementation details, and that common empirical practice leads to weak statistical evidence (Machado et al., 2018; Henderson et al., 2018). Here we take this one step further. This manuscript represents both a call to action, and a comprehensive resource for how to do good experiments in reinforcement learning. In particular, we cover: the statistical assumptions underlying common performance measures, how to properly characterize performance variation and stability, hypothesis testing, special considerations for comparing multiple agents, baseline and illustrative example construction, and how to deal with hyper-parameters and experimenter bias. Throughout we highlight common mistakes found in the literature and the statistical consequences of those in example experiments. The objective of this document is to provide answers on how we can use our unprecedented compute to do good science in reinforcement learning, as well as stay alert to potential pitfalls in our empirical design.

Robust Losses for Learning Value Functions

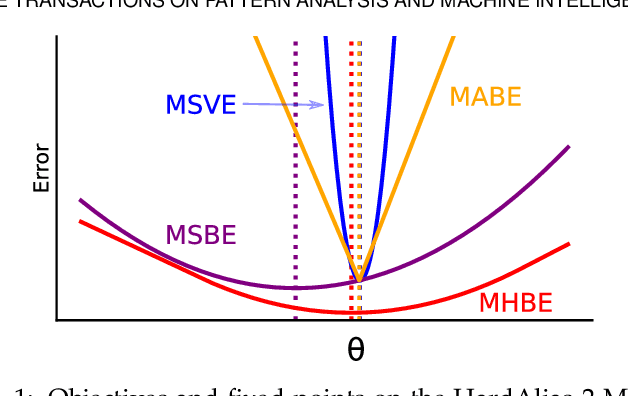
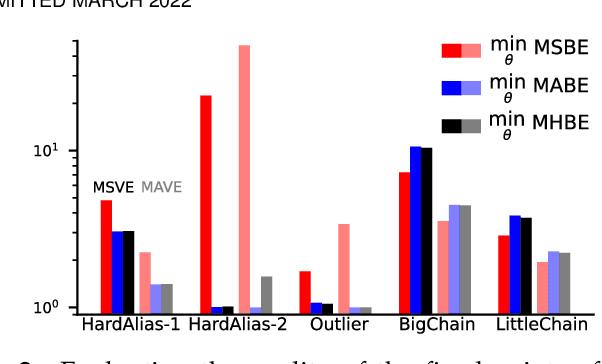
Most value function learning algorithms in reinforcement learning are based on the mean squared (projected) Bellman error. However, squared errors are known to be sensitive to outliers, both skewing the solution of the objective and resulting in high-magnitude and high-variance gradients. To control these high-magnitude updates, typical strategies in RL involve clipping gradients, clipping rewards, rescaling rewards, or clipping errors. While these strategies appear to be related to robust losses -- like the Huber loss -- they are built on semi-gradient update rules which do not minimize a known loss. In this work, we build on recent insights reformulating squared Bellman errors as a saddlepoint optimization problem and propose a saddlepoint reformulation for a Huber Bellman error and Absolute Bellman error. We start from a formalization of robust losses, then derive sound gradient-based approaches to minimize these losses in both the online off-policy prediction and control settings. We characterize the solutions of the robust losses, providing insight into the problem settings where the robust losses define notably better solutions than the mean squared Bellman error. Finally, we show that the resulting gradient-based algorithms are more stable, for both prediction and control, with less sensitivity to meta-parameters.

A Temporal-Difference Approach to Policy Gradient Estimation

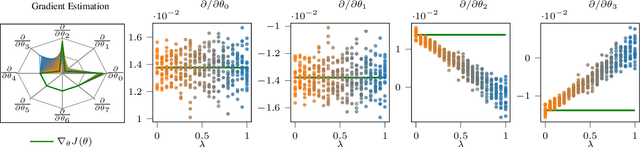
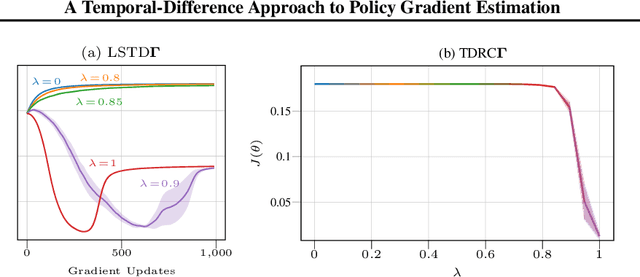
The policy gradient theorem (Sutton et al., 2000) prescribes the usage of a cumulative discounted state distribution under the target policy to approximate the gradient. Most algorithms based on this theorem, in practice, break this assumption, introducing a distribution shift that can cause the convergence to poor solutions. In this paper, we propose a new approach of reconstructing the policy gradient from the start state without requiring a particular sampling strategy. The policy gradient calculation in this form can be simplified in terms of a gradient critic, which can be recursively estimated due to a new Bellman equation of gradients. By using temporal-difference updates of the gradient critic from an off-policy data stream, we develop the first estimator that sidesteps the distribution shift issue in a model-free way. We prove that, under certain realizability conditions, our estimator is unbiased regardless of the sampling strategy. We empirically show that our technique achieves a superior bias-variance trade-off and performance in presence of off-policy samples.

A Generalized Projected Bellman Error for Off-policy Value Estimation in Reinforcement Learning

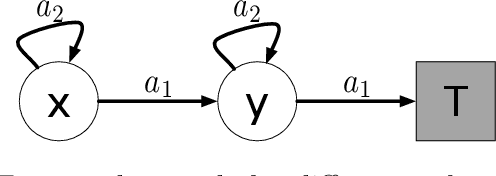
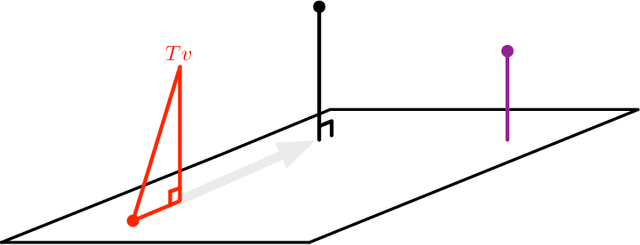
Many reinforcement learning algorithms rely on value estimation. However, the most widely used algorithms -- namely temporal difference algorithms -- can diverge under both off-policy sampling and nonlinear function approximation. Many algorithms have been developed for off-policy value estimation which are sound under linear function approximation, based on the linear mean-squared projected Bellman error (PBE). Extending these methods to the non-linear case has been largely unsuccessful. Recently, several methods have been introduced that approximate a different objective, called the mean-squared Bellman error (BE), which naturally facilities nonlinear approximation. In this work, we build on these insights and introduce a new generalized PBE, that extends the linear PBE to the nonlinear setting. We show how this generalized objective unifies previous work, including previous theory, and obtain new bounds for the value error of the solutions of the generalized objective. We derive an easy-to-use, but sound, algorithm to minimize the generalized objective which is more stable across runs, is less sensitive to hyperparameters, and performs favorably across four control domains with neural network function approximation.

$\mathcal{RL}_1$-$\mathcal{GP}$: Safe Simultaneous Learning and Control

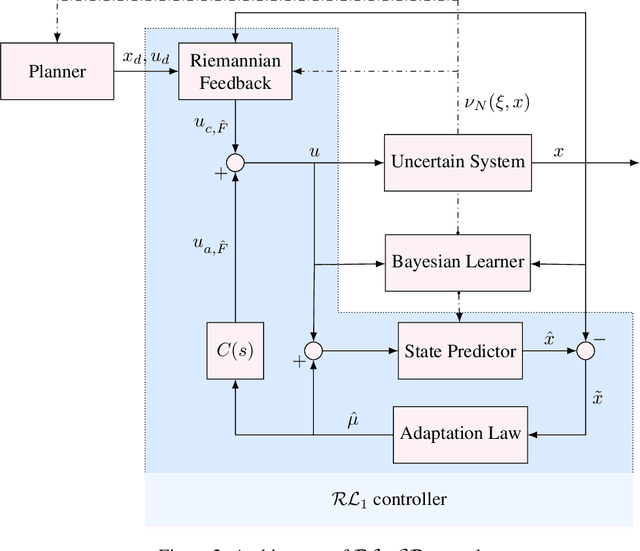
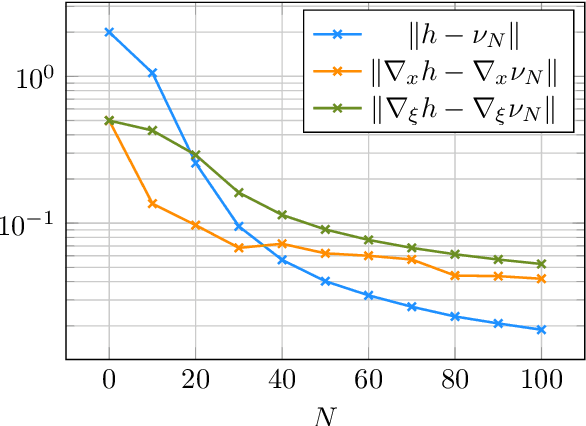
We present $\mathcal{RL}_1$-$\mathcal{GP}$, a control framework that enables safe simultaneous learning and control for systems subject to uncertainties. The two main constituents are Riemannian energy $\mathcal{L}_1$ ($\mathcal{RL}_1$) control and Bayesian learning in the form of Gaussian process (GP) regression. The $\mathcal{RL}_1$ controller ensures that control objectives are met while providing safety certificates. Furthermore, $\mathcal{RL}_1$-$\mathcal{GP}$ incorporates any available data into a GP model of uncertainties, which improves performance and enables the motion planner to achieve optimality safely. This way, the safe operation of the system is always guaranteed, even during the learning transients. We provide a few illustrative examples for the safe learning and control of planar quadrotor systems in a variety of environments.

Gradient Temporal-Difference Learning with Regularized Corrections

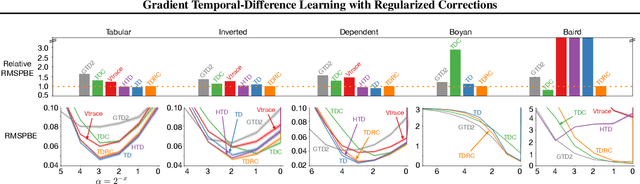
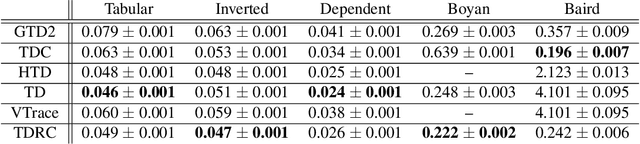
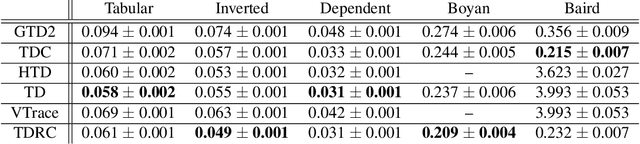
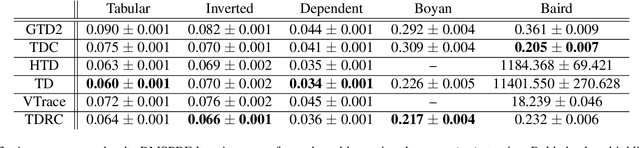
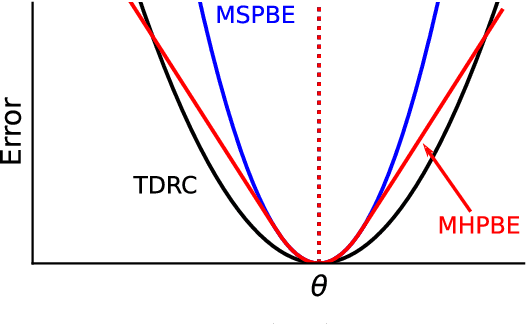
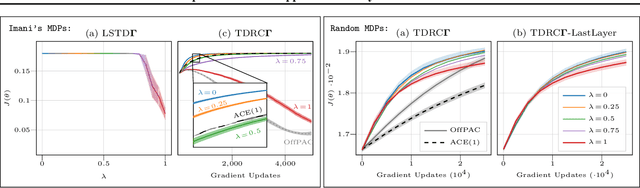
It is still common to use Q-learning and temporal difference (TD) learning-even though they have divergence issues and sound Gradient TD alternatives exist-because divergence seems rare and they typically perform well. However, recent work with large neural network learning systems reveals that instability is more common than previously thought. Practitioners face a difficult dilemma: choose an easy to use and performant TD method, or a more complex algorithm that is more sound but harder to tune and all but unexplored with non-linear function approximation or control. In this paper, we introduce a new method called TD with Regularized Corrections (TDRC), that attempts to balance ease of use, soundness, and performance. It behaves as well as TD, when TD performs well, but is sound in cases where TD diverges. We empirically investigate TDRC across a range of problems, for both prediction and control, and for both linear and non-linear function approximation, and show, potentially for the first time, that gradient TD methods could be a better alternative to TD and Q-learning.

Learning Probabilistic Intersection Traffic Models for Trajectory Prediction

Autonomous agents must be able to safely interact with other vehicles to integrate into urban environments. The safety of these agents is dependent on their ability to predict collisions with other vehicles' future trajectories for replanning and collision avoidance. The information needed to predict collisions can be learned from previously observed vehicle trajectories in a specific environment, generating a traffic model. The learned traffic model can then be incorporated as prior knowledge into any trajectory estimation method being used in this environment. This work presents a Gaussian process based probabilistic traffic model that is used to quantify vehicle behaviors in an intersection. The Gaussian process model provides estimates for the average vehicle trajectory, while also capturing the variance between the different paths a vehicle may take in the intersection. The method is demonstrated on a set of time-series position trajectories. These trajectories are reconstructed by removing object recognition errors and missed frames that may occur due to data source processing. To create the intersection traffic model, the reconstructed trajectories are clustered based on their source and destination lanes. For each cluster, a Gaussian process model is created to capture the average behavior and the variance of the cluster. To show the applicability of the Gaussian model, the test trajectories are classified with only partial observations. Performance is quantified by the number of observations required to correctly classify the vehicle trajectory. Both the intersection traffic modeling computations and the classification procedure are timed. These times are presented as results and demonstrate that the model can be constructed in a reasonable amount of time and the classification procedure can be used for online applications.