Uncertainty Estimation for 3D Object Detection via Evidential Learning

3D object detection is an essential task for computer vision applications in autonomous vehicles and robotics. However, models often struggle to quantify detection reliability, leading to poor performance on unfamiliar scenes. We introduce a framework for quantifying uncertainty in 3D object detection by leveraging an evidential learning loss on Bird's Eye View representations in the 3D detector. These uncertainty estimates require minimal computational overhead and are generalizable across different architectures. We demonstrate both the efficacy and importance of these uncertainty estimates on identifying out-of-distribution scenes, poorly localized objects, and missing (false negative) detections; our framework consistently improves over baselines by 10-20% on average. Finally, we integrate this suite of tasks into a system where a 3D object detector auto-labels driving scenes and our uncertainty estimates verify label correctness before the labels are used to train a second model. Here, our uncertainty-driven verification results in a 1% improvement in mAP and a 1-2% improvement in NDS.

Neural Spacetimes for DAG Representation Learning

We propose a class of trainable deep learning-based geometries called Neural Spacetimes (NSTs), which can universally represent nodes in weighted directed acyclic graphs (DAGs) as events in a spacetime manifold. While most works in the literature focus on undirected graph representation learning or causality embedding separately, our differentiable geometry can encode both graph edge weights in its spatial dimensions and causality in the form of edge directionality in its temporal dimensions. We use a product manifold that combines a quasi-metric (for space) and a partial order (for time). NSTs are implemented as three neural networks trained in an end-to-end manner: an embedding network, which learns to optimize the location of nodes as events in the spacetime manifold, and two other networks that optimize the space and time geometries in parallel, which we call a neural (quasi-)metric and a neural partial order, respectively. The latter two networks leverage recent ideas at the intersection of fractal geometry and deep learning to shape the geometry of the representation space in a data-driven fashion, unlike other works in the literature that use fixed spacetime manifolds such as Minkowski space or De Sitter space to embed DAGs. Our main theoretical guarantee is a universal embedding theorem, showing that any $k$-point DAG can be embedded into an NST with $1+\mathcal{O}(\log(k))$ distortion while exactly preserving its causal structure. The total number of parameters defining the NST is sub-cubic in $k$ and linear in the width of the DAG. If the DAG has a planar Hasse diagram, this is improved to $\mathcal{O}(\log(k)) + 2)$ spatial and 2 temporal dimensions. We validate our framework computationally with synthetic weighted DAGs and real-world network embeddings; in both cases, the NSTs achieve lower embedding distortions than their counterparts using fixed spacetime geometries.

Breaking the Curse of Dimensionality with Distributed Neural Computation

We present a theoretical approach to overcome the curse of dimensionality using a neural computation algorithm which can be distributed across several machines. Our modular distributed deep learning paradigm, termed \textit{neural pathways}, can achieve arbitrary accuracy while only loading a small number of parameters into GPU VRAM. Formally, we prove that for every error level $\varepsilon>0$ and every Lipschitz function $f:[0,1]^n\to \mathbb{R}$, one can construct a neural pathways model which uniformly approximates $f$ to $\varepsilon$ accuracy over $[0,1]^n$ while only requiring networks of $\mathcal{O}(\varepsilon^{-1})$ parameters to be loaded in memory and $\mathcal{O}(\varepsilon^{-1}\log(\varepsilon^{-1}))$ to be loaded during the forward pass. This improves the optimal bounds for traditional non-distributed deep learning models, namely ReLU MLPs, which need $\mathcal{O}(\varepsilon^{-n/2})$ parameters to achieve the same accuracy. The only other available deep learning model that breaks the curse of dimensionality is MLPs with super-expressive activation functions. However, we demonstrate that these models have an infinite VC dimension, even with bounded depth and width restrictions, unlike the neural pathways model. This implies that only the latter generalizes. Our analysis is validated experimentally in both regression and classification tasks, demonstrating that our model exhibits superior performance compared to larger centralized benchmarks.

Graph Metanetworks for Processing Diverse Neural Architectures

Neural networks efficiently encode learned information within their parameters. Consequently, many tasks can be unified by treating neural networks themselves as input data. When doing so, recent studies demonstrated the importance of accounting for the symmetries and geometry of parameter spaces. However, those works developed architectures tailored to specific networks such as MLPs and CNNs without normalization layers, and generalizing such architectures to other types of networks can be challenging. In this work, we overcome these challenges by building new metanetworks - neural networks that take weights from other neural networks as input. Put simply, we carefully build graphs representing the input neural networks and process the graphs using graph neural networks. Our approach, Graph Metanetworks (GMNs), generalizes to neural architectures where competing methods struggle, such as multi-head attention layers, normalization layers, convolutional layers, ResNet blocks, and group-equivariant linear layers. We prove that GMNs are expressive and equivariant to parameter permutation symmetries that leave the input neural network functions unchanged. We validate the effectiveness of our method on several metanetwork tasks over diverse neural network architectures.

Bridging the Sim2Real gap with CARE: Supervised Detection Adaptation with Conditional Alignment and Reweighting

Sim2Real domain adaptation (DA) research focuses on the constrained setting of adapting from a labeled synthetic source domain to an unlabeled or sparsely labeled real target domain. However, for high-stakes applications (e.g. autonomous driving), it is common to have a modest amount of human-labeled real data in addition to plentiful auto-labeled source data (e.g. from a driving simulator). We study this setting of supervised sim2real DA applied to 2D object detection. We propose Domain Translation via Conditional Alignment and Reweighting (CARE) a novel algorithm that systematically exploits target labels to explicitly close the sim2real appearance and content gaps. We present an analytical justification of our algorithm and demonstrate strong gains over competing methods on standard benchmarks.

Optimizing Data Collection for Machine Learning

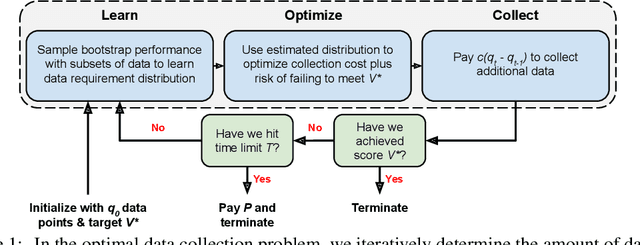
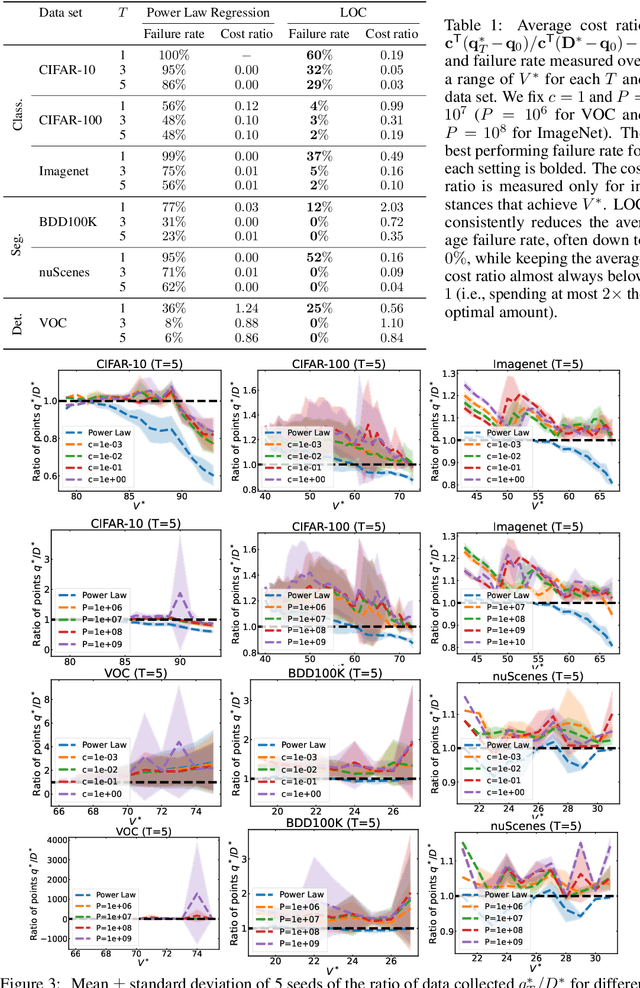
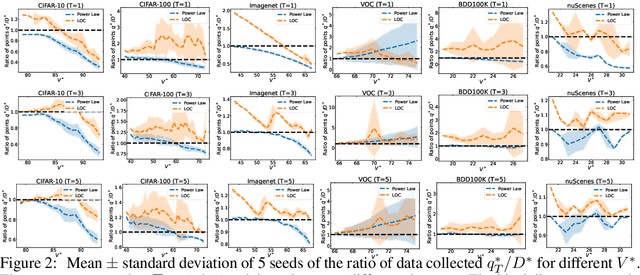
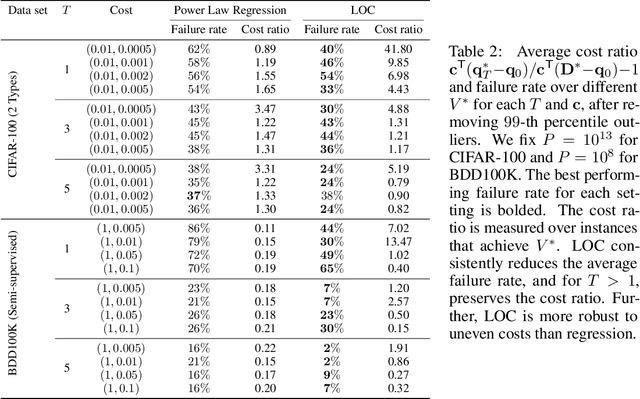
Modern deep learning systems require huge data sets to achieve impressive performance, but there is little guidance on how much or what kind of data to collect. Over-collecting data incurs unnecessary present costs, while under-collecting may incur future costs and delay workflows. We propose a new paradigm for modeling the data collection workflow as a formal optimal data collection problem that allows designers to specify performance targets, collection costs, a time horizon, and penalties for failing to meet the targets. Additionally, this formulation generalizes to tasks requiring multiple data sources, such as labeled and unlabeled data used in semi-supervised learning. To solve our problem, we develop Learn-Optimize-Collect (LOC), which minimizes expected future collection costs. Finally, we numerically compare our framework to the conventional baseline of estimating data requirements by extrapolating from neural scaling laws. We significantly reduce the risks of failing to meet desired performance targets on several classification, segmentation, and detection tasks, while maintaining low total collection costs.

How Much More Data Do I Need? Estimating Requirements for Downstream Tasks

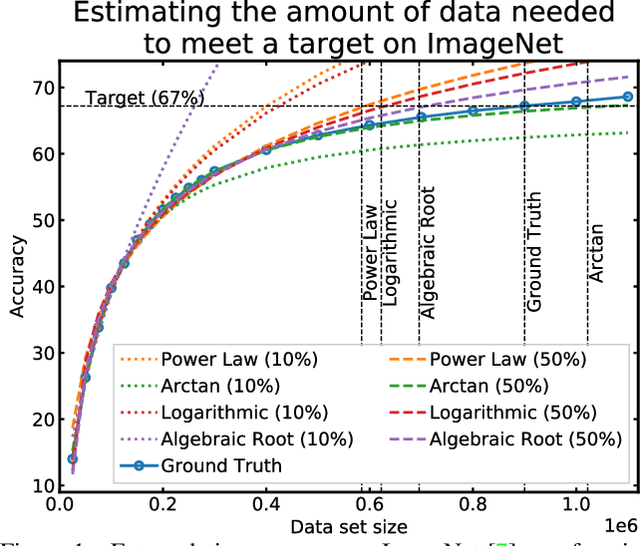
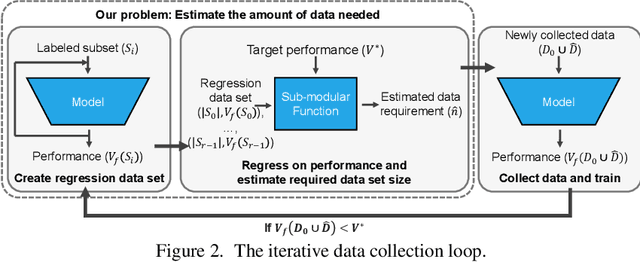
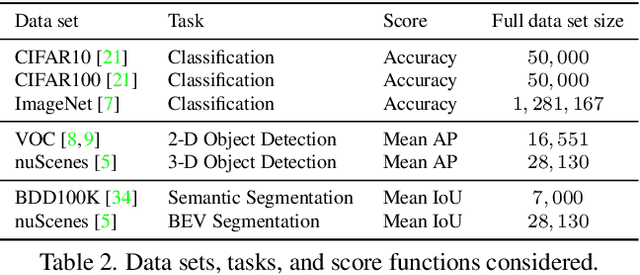
Given a small training data set and a learning algorithm, how much more data is necessary to reach a target validation or test performance? This question is of critical importance in applications such as autonomous driving or medical imaging where collecting data is expensive and time-consuming. Overestimating or underestimating data requirements incurs substantial costs that could be avoided with an adequate budget. Prior work on neural scaling laws suggest that the power-law function can fit the validation performance curve and extrapolate it to larger data set sizes. We find that this does not immediately translate to the more difficult downstream task of estimating the required data set size to meet a target performance. In this work, we consider a broad class of computer vision tasks and systematically investigate a family of functions that generalize the power-law function to allow for better estimation of data requirements. Finally, we show that incorporating a tuned correction factor and collecting over multiple rounds significantly improves the performance of the data estimators. Using our guidelines, practitioners can accurately estimate data requirements of machine learning systems to gain savings in both development time and data acquisition costs.

Feature Generation for Long-tail Classification

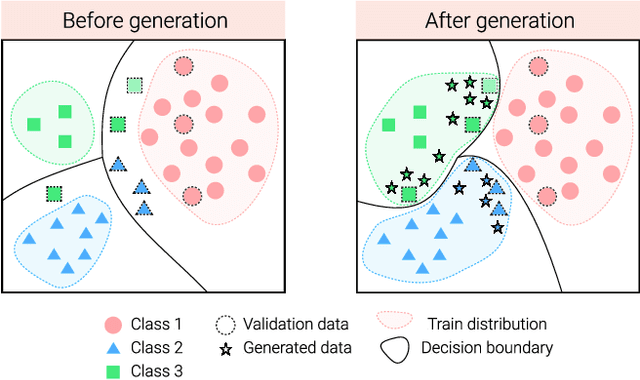
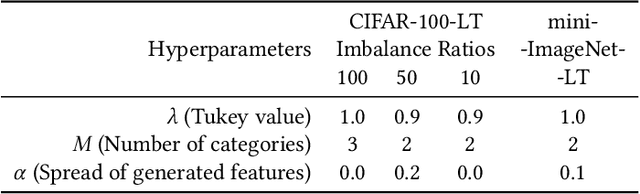
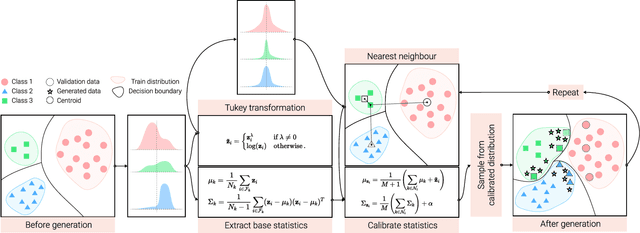
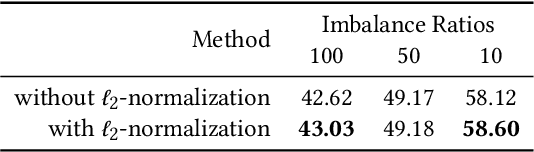
The visual world naturally exhibits an imbalance in the number of object or scene instances resulting in a \emph{long-tailed distribution}. This imbalance poses significant challenges for classification models based on deep learning. Oversampling instances of the tail classes attempts to solve this imbalance. However, the limited visual diversity results in a network with poor representation ability. A simple counter to this is decoupling the representation and classifier networks and using oversampling only to train the classifier. In this paper, instead of repeatedly re-sampling the same image (and thereby features), we explore a direction that attempts to generate meaningful features by estimating the tail category's distribution. Inspired by ideas from recent work on few-shot learning, we create calibrated distributions to sample additional features that are subsequently used to train the classifier. Through several experiments on the CIFAR-100-LT (long-tail) dataset with varying imbalance factors and on mini-ImageNet-LT (long-tail), we show the efficacy of our approach and establish a new state-of-the-art. We also present a qualitative analysis of generated features using t-SNE visualizations and analyze the nearest neighbors used to calibrate the tail class distributions. Our code is available at https://github.com/rahulvigneswaran/TailCalibX.

f-Domain-Adversarial Learning: Theory and Algorithms

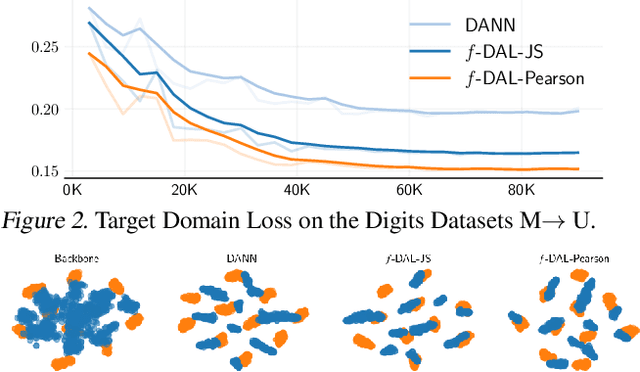
Unsupervised domain adaptation is used in many machine learning applications where, during training, a model has access to unlabeled data in the target domain, and a related labeled dataset. In this paper, we introduce a novel and general domain-adversarial framework. Specifically, we derive a novel generalization bound for domain adaptation that exploits a new measure of discrepancy between distributions based on a variational characterization of f-divergences. It recovers the theoretical results from Ben-David et al. (2010a) as a special case and supports divergences used in practice. Based on this bound, we derive a new algorithmic framework that introduces a key correction in the original adversarial training method of Ganin et al. (2016). We show that many regularizers and ad-hoc objectives introduced over the last years in this framework are then not required to achieve performance comparable to (if not better than) state-of-the-art domain-adversarial methods. Experimental analysis conducted on real-world natural language and computer vision datasets show that our framework outperforms existing baselines, and obtains the best results for f-divergences that were not considered previously in domain-adversarial learning.

Low Budget Active Learning via Wasserstein Distance: An Integer Programming Approach

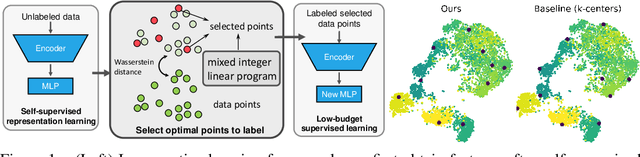
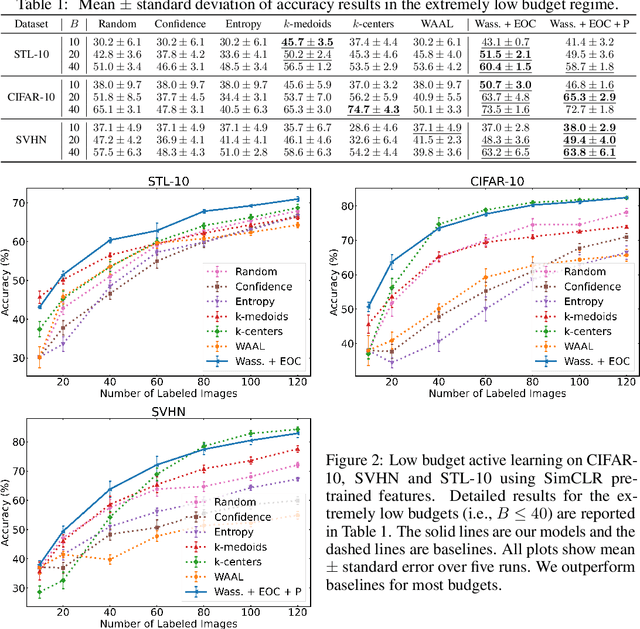
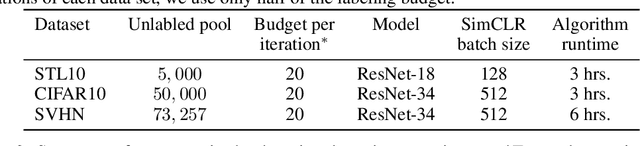
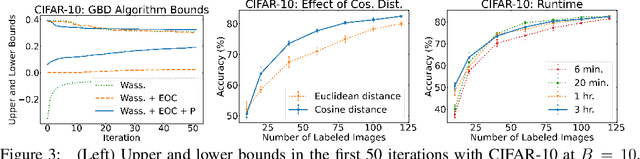
Given restrictions on the availability of data, active learning is the process of training a model with limited labeled data by selecting a core subset of an unlabeled data pool to label. Although selecting the most useful points for training is an optimization problem, the scale of deep learning data sets forces most selection strategies to employ efficient heuristics. Instead, we propose a new integer optimization problem for selecting a core set that minimizes the discrete Wasserstein distance from the unlabeled pool. We demonstrate that this problem can be tractably solved with a Generalized Benders Decomposition algorithm. Our strategy requires high-quality latent features which we obtain by unsupervised learning on the unlabeled pool. Numerical results on several data sets show that our optimization approach is competitive with baselines and particularly outperforms them in the low budget regime where less than one percent of the data set is labeled.