How to design a dataset compliant with an ML-based system ODD?

This paper focuses on a Vision-based Landing task and presents the design and the validation of a dataset that would comply with the Operational Design Domain (ODD) of a Machine-Learning (ML) system. Relying on emerging certification standards, we describe the process for establishing ODDs at both the system and image levels. In the process, we present the translation of high-level system constraints into actionable image-level properties, allowing for the definition of verifiable Data Quality Requirements (DQRs). To illustrate this approach, we use the Landing Approach Runway Detection (LARD) dataset which combines synthetic imagery and real footage, and we focus on the steps required to verify the DQRs. The replicable framework presented in this paper addresses the challenges of designing a dataset compliant with the stringent needs of ML-based systems certification in safety-critical applications.

Surrogate Neural Networks Local Stability for Aircraft Predictive Maintenance

Surrogate Neural Networks (NN) now routinely serve as substitutes for computationally demanding simulations (e.g., finite element). They enable faster analyses in industrial applications e.g., manufacturing processes, performance assessment. The verification of surrogate models is a critical step to assess their robustness under different scenarios. We explore the combination of empirical and formal methods in one NN verification pipeline. We showcase its efficiency on an industrial use case of aircraft predictive maintenance. We assess the local stability of surrogate NN designed to predict the stress sustained by an aircraft part from external loads. Our contribution lies in the complete verification of the surrogate models that possess a high-dimensional input and output space, thus accommodating multi-objective constraints. We also demonstrate the pipeline effectiveness in substantially decreasing the runtime needed to assess the targeted property.

Robustness Assessment of a Runway Object Classifier for Safe Aircraft Taxiing

As deep neural networks (DNNs) are becoming the prominent solution for many computational problems, the aviation industry seeks to explore their potential in alleviating pilot workload and in improving operational safety. However, the use of DNNs in this type of safety-critical applications requires a thorough certification process. This need can be addressed through formal verification, which provides rigorous assurances -- e.g.,~by proving the absence of certain mispredictions. In this case-study paper, we demonstrate this process using an image-classifier DNN currently under development at Airbus and intended for use during the aircraft taxiing phase. We use formal methods to assess this DNN's robustness to three common image perturbation types: noise, brightness and contrast, and some of their combinations. This process entails multiple invocations of the underlying verifier, which might be computationally expensive; and we therefore propose a method that leverages the monotonicity of these robustness properties, as well as the results of past verification queries, in order to reduce the overall number of verification queries required by nearly 60%. Our results provide an indication of the level of robustness achieved by the DNN classifier under study, and indicate that it is considerably more vulnerable to noise than to brightness or contrast perturbations.

LARD -- Landing Approach Runway Detection -- Dataset for Vision Based Landing

As the interest in autonomous systems continues to grow, one of the major challenges is collecting sufficient and representative real-world data. Despite the strong practical and commercial interest in autonomous landing systems in the aerospace field, there is a lack of open-source datasets of aerial images. To address this issue, we present a dataset-lard-of high-quality aerial images for the task of runway detection during approach and landing phases. Most of the dataset is composed of synthetic images but we also provide manually labelled images from real landing footages, to extend the detection task to a more realistic setting. In addition, we offer the generator which can produce such synthetic front-view images and enables automatic annotation of the runway corners through geometric transformations. This dataset paves the way for further research such as the analysis of dataset quality or the development of models to cope with the detection tasks. Find data, code and more up-to-date information at https://github.com/deel-ai/LARD

Overestimation learning with guarantees

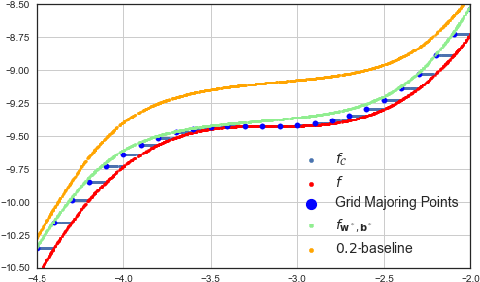
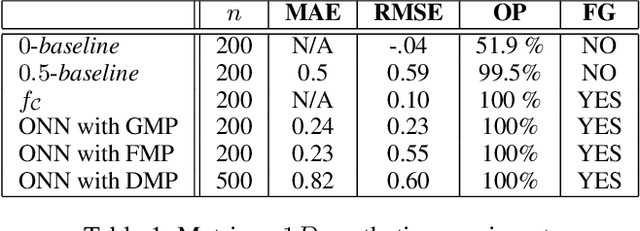
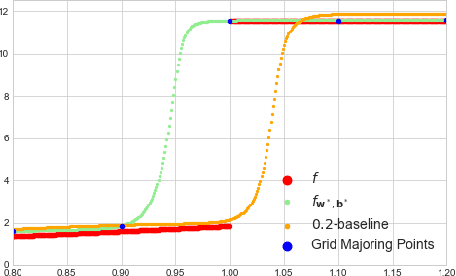
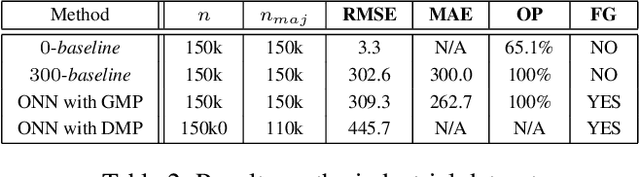
We describe a complete method that learns a neural network which is guaranteed to overestimate a reference function on a given domain. The neural network can then be used as a surrogate for the reference function. The method involves two steps. In the first step, we construct an adaptive set of Majoring Points. In the second step, we optimize a well-chosen neural network to overestimate the Majoring Points. In order to extend the guarantee on the Majoring Points to the whole domain, we necessarily have to make an assumption on the reference function. In this study, we assume that the reference function is monotonic. We provide experiments on synthetic and real problems. The experiments show that the density of the Majoring Points concentrate where the reference function varies. The learned over-estimations are both guaranteed to overestimate the reference function and are proven empirically to provide good approximations of it. Experiments on real data show that the method makes it possible to use the surrogate function in embedded systems for which an underestimation is critical; when computing the reference function requires too many resources.

Time Series to Images: Monitoring the Condition of Industrial Assets with Deep Learning Image Processing Algorithms

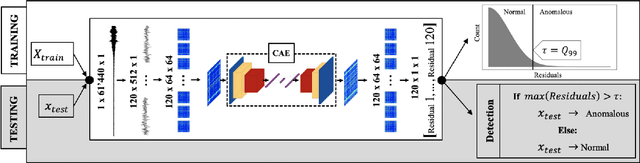
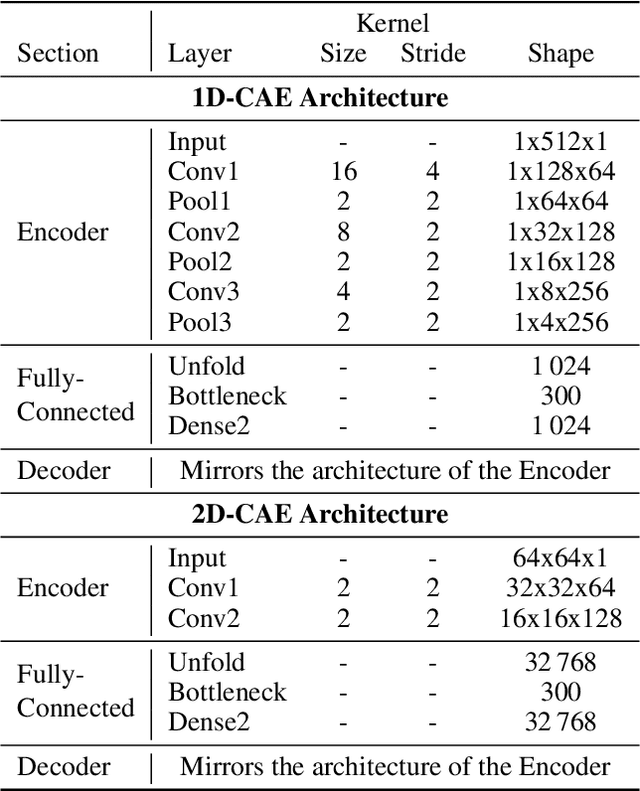
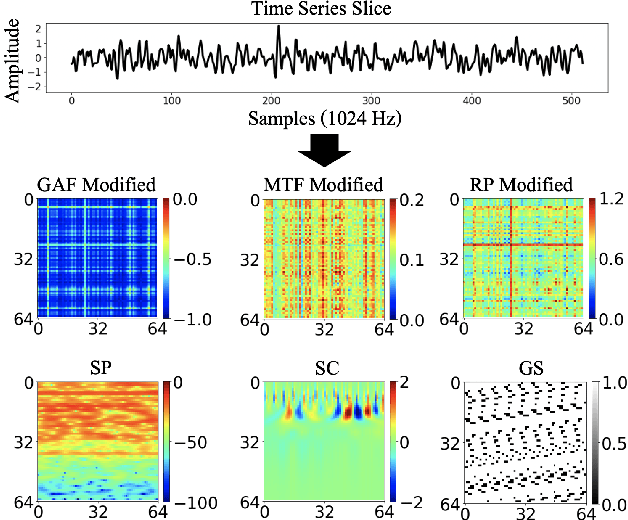
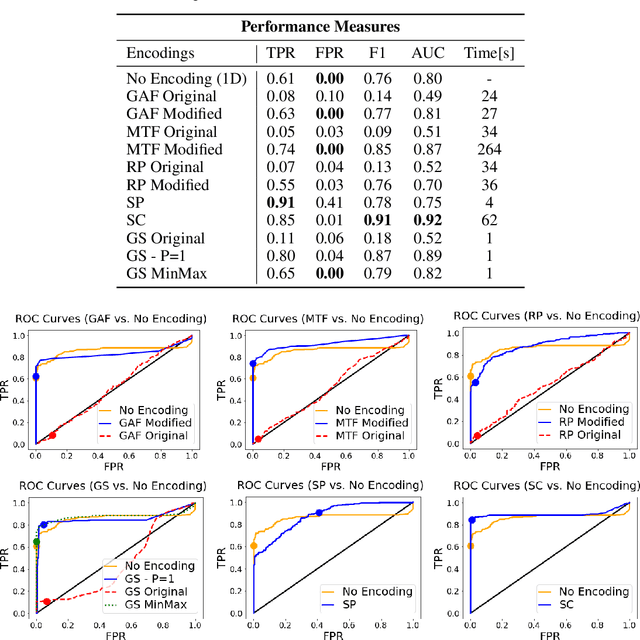
The ability to detect anomalies in time series is considered as highly valuable within plenty of application domains. The sequential nature of time series objects is responsible for an additional feature complexity, ultimately requiring specialized approaches for solving the task. Essential characteristics of time series, laying outside the time domain, are often difficult to capture with state-of-the-art anomaly detection methods, when no transformations on the time series have been applied. Inspired by the success of deep learning methods in computer vision, several studies have proposed to transform time-series into image-like representations, leading to very promising results. However, most of the previous studies implementing time-series to image encodings have focused on the supervised classification. The application to unsupervised anomaly detection tasks has been limited. The paper has the following contributions: First, we evaluate the application of six time-series to image encodings to DL algorithms: Gramian Angular Field, Markov Transition Field, Recurrence Plot, Grey Scale Encoding, Spectrogram and Scalogram. Second, we propose modifications of the original encoding definitions, to make them more robust to the variability in large datasets. And third, we provide a comprehensive comparison between using the raw time series directly and the different encodings, with and without the proposed improvements. The comparison is performed on a dataset collected and released by Airbus, containing highly complex vibration measurements from real helicopters flight tests. The different encodings provide competitive results for anomaly detection.

Learning Wasserstein Embeddings

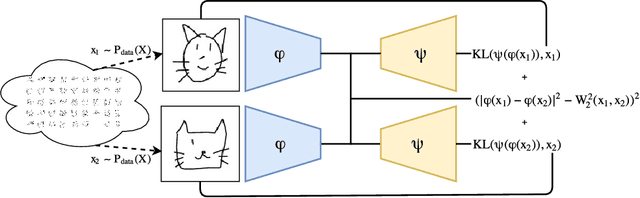
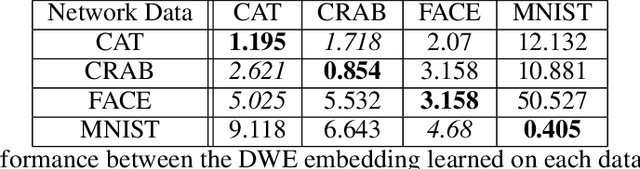
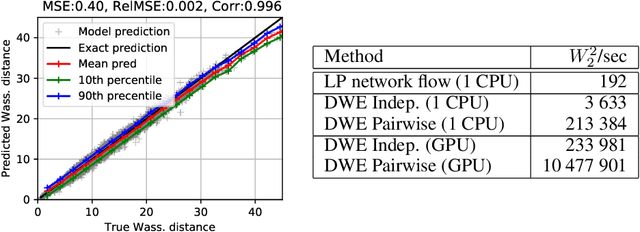
The Wasserstein distance received a lot of attention recently in the community of machine learning, especially for its principled way of comparing distributions. It has found numerous applications in several hard problems, such as domain adaptation, dimensionality reduction or generative models. However, its use is still limited by a heavy computational cost. Our goal is to alleviate this problem by providing an approximation mechanism that allows to break its inherent complexity. It relies on the search of an embedding where the Euclidean distance mimics the Wasserstein distance. We show that such an embedding can be found with a siamese architecture associated with a decoder network that allows to move from the embedding space back to the original input space. Once this embedding has been found, computing optimization problems in the Wasserstein space (e.g. barycenters, principal directions or even archetypes) can be conducted extremely fast. Numerical experiments supporting this idea are conducted on image datasets, and show the wide potential benefits of our method.

Theano: A Python framework for fast computation of mathematical expressions

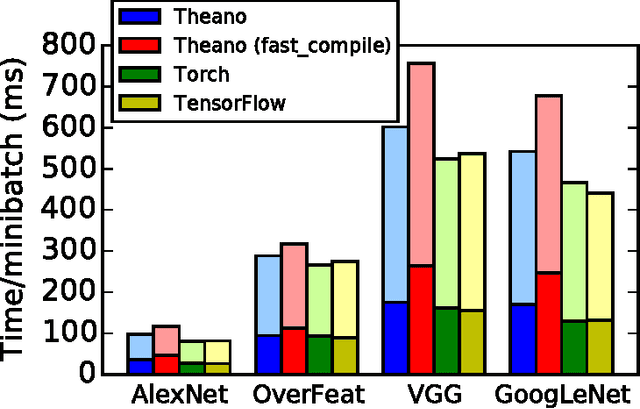
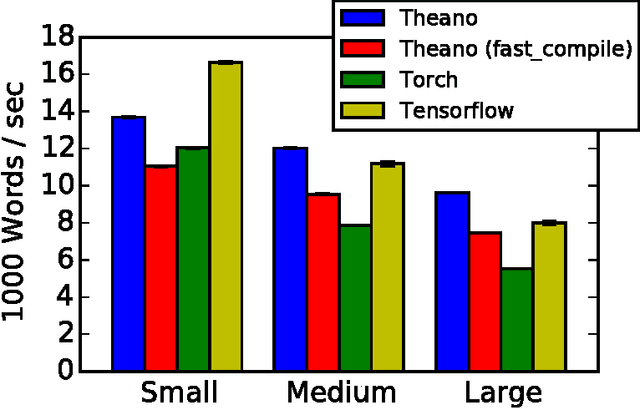
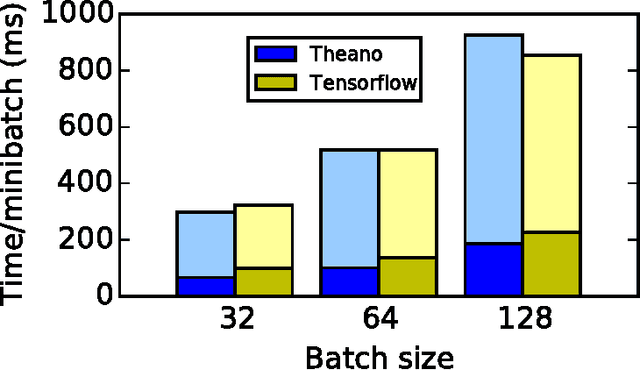
Theano is a Python library that allows to define, optimize, and evaluate mathematical expressions involving multi-dimensional arrays efficiently. Since its introduction, it has been one of the most used CPU and GPU mathematical compilers - especially in the machine learning community - and has shown steady performance improvements. Theano is being actively and continuously developed since 2008, multiple frameworks have been built on top of it and it has been used to produce many state-of-the-art machine learning models. The present article is structured as follows. Section I provides an overview of the Theano software and its community. Section II presents the principal features of Theano and how to use them, and compares them with other similar projects. Section III focuses on recently-introduced functionalities and improvements. Section IV compares the performance of Theano against Torch7 and TensorFlow on several machine learning models. Section V discusses current limitations of Theano and potential ways of improving it.