A Mathematical Explanation of UNet

The UNet architecture has transformed image segmentation. UNet's versatility and accuracy have driven its widespread adoption, significantly advancing fields reliant on machine learning problems with images. In this work, we give a clear and concise mathematical explanation of UNet. We explain what is the meaning and function of each of the components of UNet. We will show that UNet is solving a control problem. We decompose the control variables using multigrid methods. Then, operator-splitting techniques is used to solve the problem, whose architecture exactly recovers the UNet architecture. Our result shows that UNet is a one-step operator-splitting algorithm for the control problem.

BP-DeepONet: A new method for cuffless blood pressure estimation using the physcis-informed DeepONet

Cardiovascular diseases (CVDs) are the leading cause of death worldwide, with blood pressure serving as a crucial indicator. Arterial blood pressure (ABP) waveforms provide continuous pressure measurements throughout the cardiac cycle and offer valuable diagnostic insights. Consequently, there is a significant demand for non-invasive and cuff-less methods to measure ABP waveforms continuously. Accurate prediction of ABP waveforms can also improve the estimation of mean blood pressure, an essential cardiovascular health characteristic. This study proposes a novel framework based on the physics-informed DeepONet approach to predict ABP waveforms. Unlike previous methods, our approach requires the predicted ABP waveforms to satisfy the Navier-Stokes equation with a time-periodic condition and a Windkessel boundary condition. Notably, our framework is the first to predict ABP waveforms continuously, both with location and time, within the part of the artery that is being simulated. Furthermore, our method only requires ground truth data at the outlet boundary and can handle periodic conditions with varying periods. Incorporating the Windkessel boundary condition in our solution allows for generating natural physical reflection waves, which closely resemble measurements observed in real-world cases. Moreover, accurately estimating the hyper-parameters in the Navier-Stokes equation for our simulations poses a significant challenge. To overcome this obstacle, we introduce the concept of meta-learning, enabling the neural networks to learn these parameters during the training process.

Structure Regularized Attentive Network for Automatic Femoral Head Necrosis Diagnosis and Localization

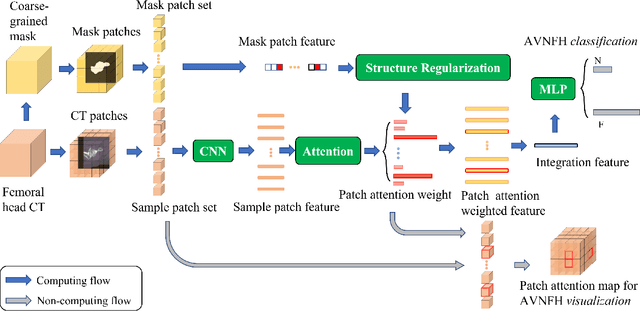
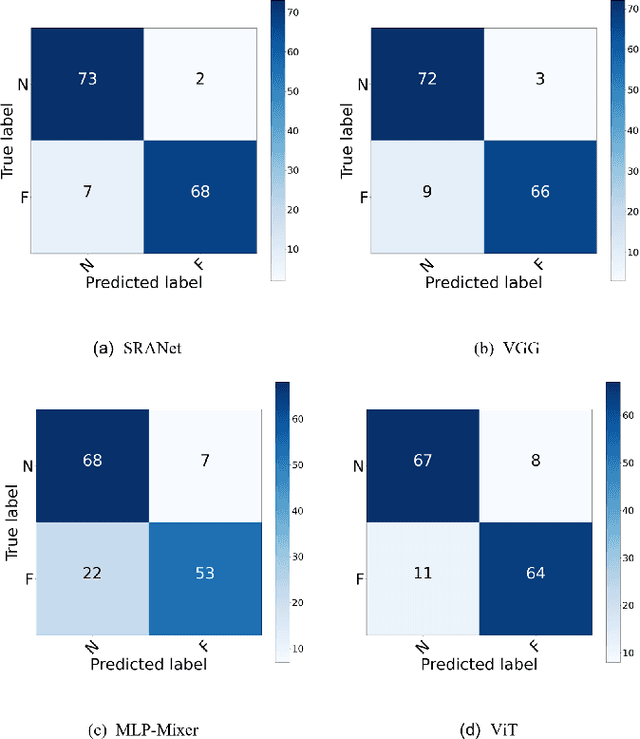
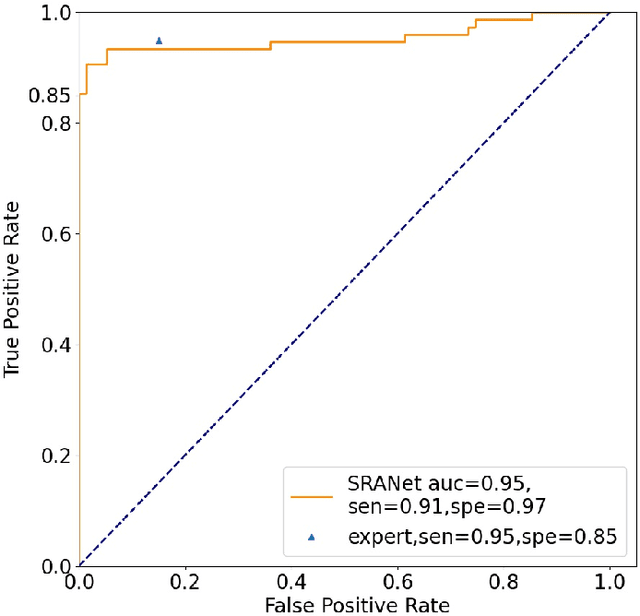
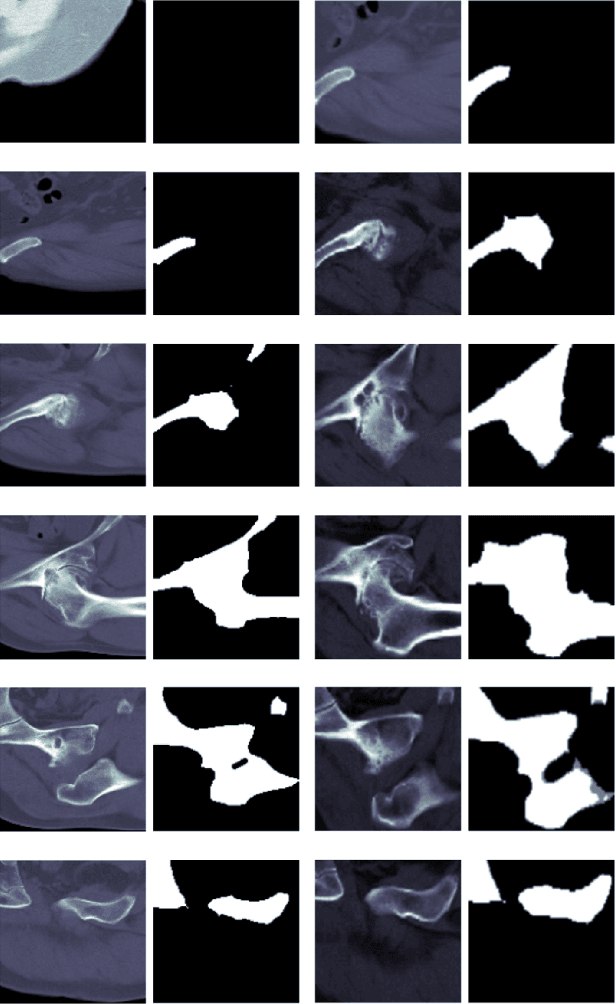
In recent years, several works have adopted the convolutional neural network (CNN) to diagnose the avascular necrosis of the femoral head (AVNFH) based on X-ray images or magnetic resonance imaging (MRI). However, due to the tissue overlap, X-ray images are difficult to provide fine-grained features for early diagnosis. MRI, on the other hand, has a long imaging time, is more expensive, making it impractical in mass screening. Computed tomography (CT) shows layer-wise tissues, is faster to image, and is less costly than MRI. However, to our knowledge, there is no work on CT-based automated diagnosis of AVNFH. In this work, we collected and labeled a large-scale dataset for AVNFH ranking. In addition, existing end-to-end CNNs only yields the classification result and are difficult to provide more information for doctors in diagnosis. To address this issue, we propose the structure regularized attentive network (SRANet), which is able to highlight the necrotic regions during classification based on patch attention. SRANet extracts features in chunks of images, obtains weight via the attention mechanism to aggregate the features, and constrains them by a structural regularizer with prior knowledge to improve the generalization. SRANet was evaluated on our AVNFH-CT dataset. Experimental results show that SRANet is superior to CNNs for AVNFH classification, moreover, it can localize lesions and provide more information to assist doctors in diagnosis. Our codes are made public at https://github.com/tomas-lilingfeng/SRANet.

Generalization Error Analysis of Neural networks with Gradient Based Regularization

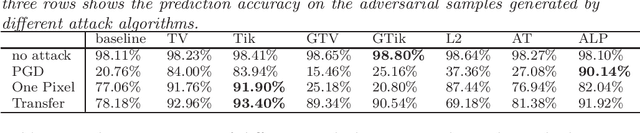
We study gradient-based regularization methods for neural networks. We mainly focus on two regularization methods: the total variation and the Tikhonov regularization. Applying these methods is equivalent to using neural networks to solve some partial differential equations, mostly in high dimensions in practical applications. In this work, we introduce a general framework to analyze the generalization error of regularized networks. The error estimate relies on two assumptions on the approximation error and the quadrature error. Moreover, we conduct some experiments on the image classification tasks to show that gradient-based methods can significantly improve the generalization ability and adversarial robustness of neural networks. A graphical extension of the gradient-based methods are also considered in the experiments.

Deep Multi-task Prediction of Lung Cancer and Cancer-free Progression from Censored Heterogenous Clinical Imaging

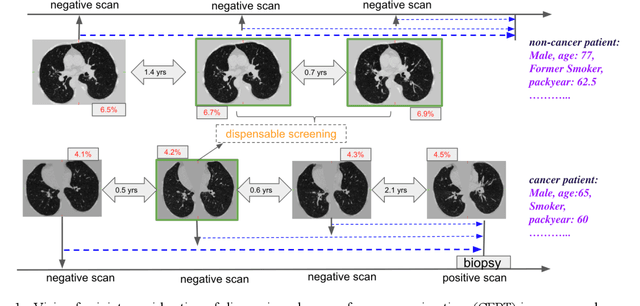
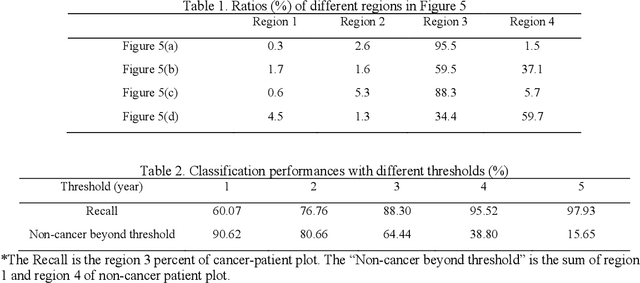
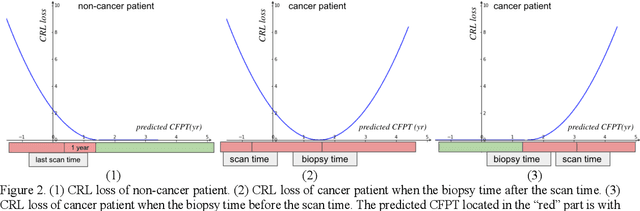
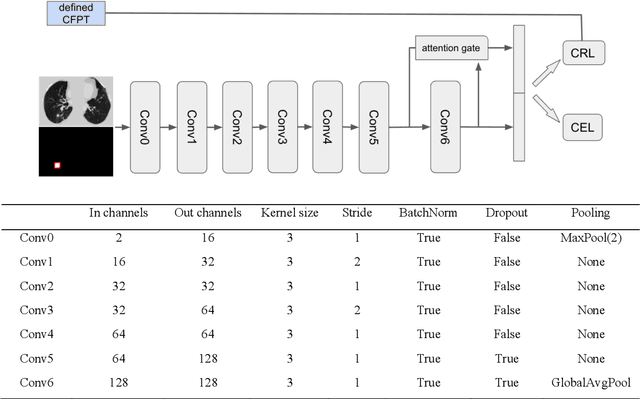
Annual low dose computed tomography (CT) lung screening is currently advised for individuals at high risk of lung cancer (e.g., heavy smokers between 55 and 80 years old). The recommended screening practice significantly reduces all-cause mortality, but the vast majority of screening results are negative for cancer. If patients at very low risk could be identified based on individualized, image-based biomarkers, the health care resources could be more efficiently allocated to higher risk patients and reduce overall exposure to ionizing radiation. In this work, we propose a multi-task (diagnosis and prognosis) deep convolutional neural network to improve the diagnostic accuracy over a baseline model while simultaneously estimating a personalized cancer-free progression time (CFPT). A novel Censored Regression Loss (CRL) is proposed to perform weakly supervised regression so that even single negative screening scans can provide small incremental value. Herein, we study 2287 scans from 1433 de-identified patients from the Vanderbilt Lung Screening Program (VLSP) and Molecular Characterization Laboratories (MCL) cohorts. Using five-fold cross-validation, we train a 3D attention-based network under two scenarios: (1) single-task learning with only classification, and (2) multi-task learning with both classification and regression. The single-task learning leads to a higher AUC compared with the Kaggle challenge winner pre-trained model (0.878 v. 0.856), and multi-task learning significantly improves the single-task one (AUC 0.895, p<0.01, McNemar test). In summary, the image-based predicted CFPT can be used in follow-up year lung cancer prediction and data assessment.

Convex hull algorithms based on some variational models

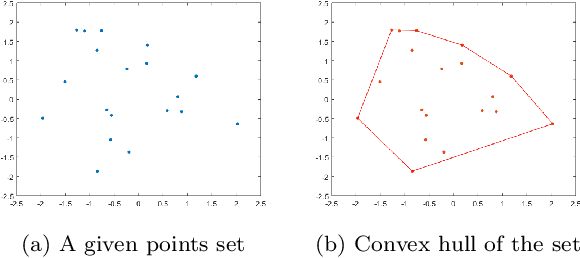
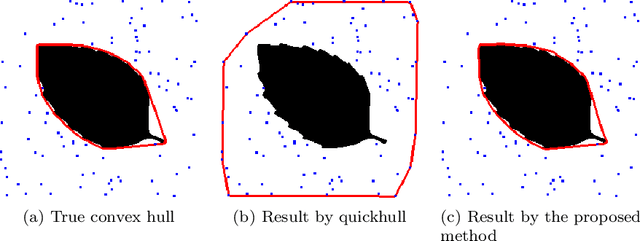
Seeking the convex hull of an object is a very fundamental problem arising from various tasks. In this work, we propose two variational convex hull models using level set representation for 2-dimensional data. The first one is an exact model, which can get the convex hull of one or multiple objects. In this model, the convex hull is characterized by the zero sublevel-set of a convex level set function, which is non-positive at every given point. By minimizing the area of the zero sublevel-set, we can find the desired convex hull. The second one is intended to get convex hull of objects with outliers. Instead of requiring all the given points are included, this model penalizes the distance from each given point to the zero sublevel-set. Literature methods are not able to handle outliers. For the solution of these models, we develop efficient numerical schemes using alternating direction method of multipliers. Numerical examples are given to demonstrate the advantages of the proposed methods.