Multiple Convex Objects Image Segmentation via Proximal Alternating Direction Method of Multipliers

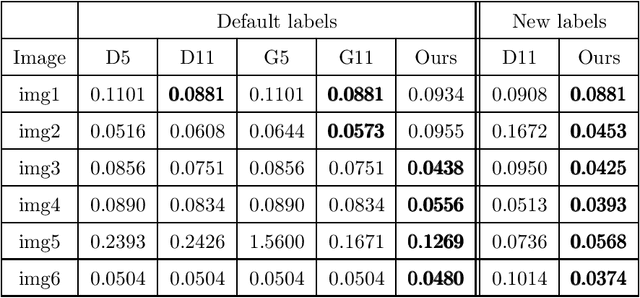
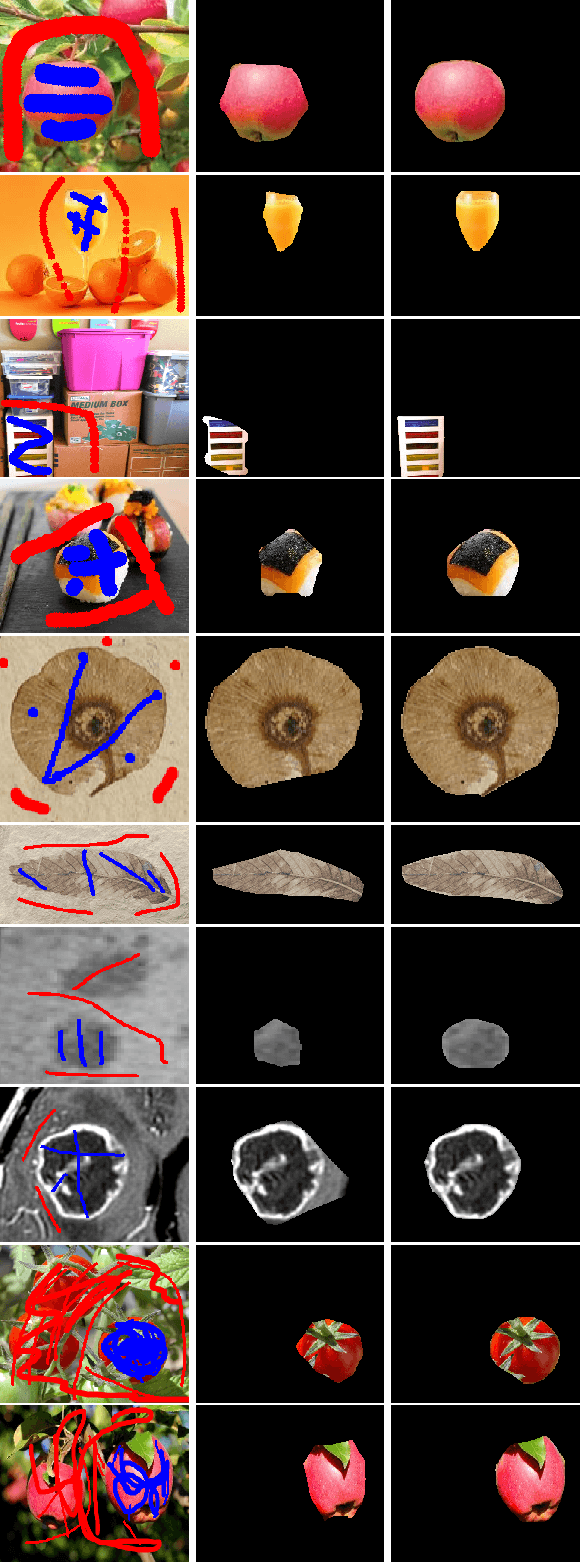
This paper focuses on the issue of image segmentation with convex shape prior. Firstly, we use binary function to represent convex object(s). The convex shape prior turns out to be a simple quadratic inequality constraint on the binary indicator function associated with each object. An image segmentation model incorporating convex shape prior into a probability-based method is proposed. Secondly, a new algorithm is designed to solve involved optimization problem, which is a challenging task because of the quadratic inequality constraint. To tackle this difficulty, we relax and linearize the quadratic inequality constraint to reduce it to solve a sequence of convex minimization problems. For each convex problem, an efficient proximal alternating direction method of multipliers is developed to solve it. The convergence of the algorithm follows some existing results in the optimization literature. Moreover, an interactive procedure is introduced to improve the accuracy of segmentation gradually. Numerical experiments on natural and medical images demonstrate that the proposed method is superior to some existing methods in terms of segmentation accuracy and computational time.

Convex Shape Prior for Deep Neural Convolution Network based Eye Fundus Images Segmentation

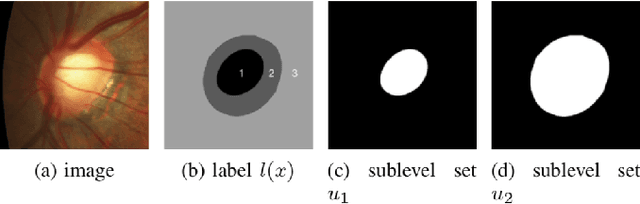
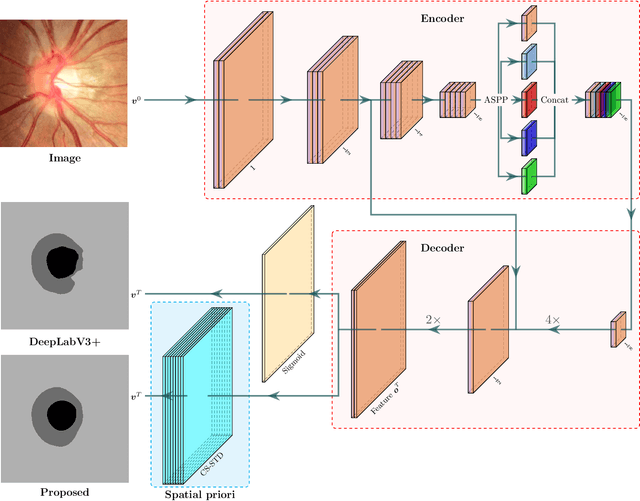
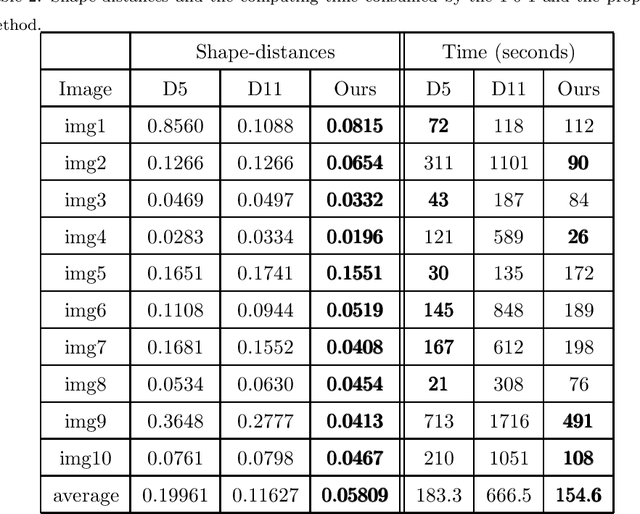
Convex Shapes (CS) are common priors for optic disc and cup segmentation in eye fundus images. It is important to design proper techniques to represent convex shapes. So far, it is still a problem to guarantee that the output objects from a Deep Neural Convolution Networks (DCNN) are convex shapes. In this work, we propose a technique which can be easily integrated into the commonly used DCNNs for image segmentation and guarantee that outputs are convex shapes. This method is flexible and it can handle multiple objects and allow some of the objects to be convex. Our method is based on the dual representation of the sigmoid activation function in DCNNs. In the dual space, the convex shape prior can be guaranteed by a simple quadratic constraint on a binary representation of the shapes. Moreover, our method can also integrate spatial regularization and some other shape prior using a soft thresholding dynamics (STD) method. The regularization can make the boundary curves of the segmentation objects to be simultaneously smooth and convex. We design a very stable active set projection algorithm to numerically solve our model. This algorithm can form a new plug-and-play DCNN layer called CS-STD whose outputs must be a nearly binary segmentation of convex objects. In the CS-STD block, the convexity information can be propagated to guide the DCNN in both forward and backward propagation during training and prediction process. As an application example, we apply the convexity prior layer to the retinal fundus images segmentation by taking the popular DeepLabV3+ as a backbone network. Experimental results on several public datasets show that our method is efficient and outperforms the classical DCNN segmentation methods.

A level set representation method for N-dimensional convex shape and applications

In this work, we present a new efficient method for convex shape representation, which is regardless of the dimension of the concerned objects, using level-set approaches. Convexity prior is very useful for object completion in computer vision. It is a very challenging task to design an efficient method for high dimensional convex objects representation. In this paper, we prove that the convexity of the considered object is equivalent to the convexity of the associated signed distance function. Then, the second order condition of convex functions is used to characterize the shape convexity equivalently. We apply this new method to two applications: object segmentation with convexity prior and convex hull problem (especially with outliers). For both applications, the involved problems can be written as a general optimization problem with three constraints. Efficient algorithm based on alternating direction method of multipliers is presented for the optimization problem. Numerical experiments are conducted to verify the effectiveness and efficiency of the proposed representation method and algorithm.

Convex Shape Representation with Binary Labels for Image Segmentation: Models and Fast Algorithms

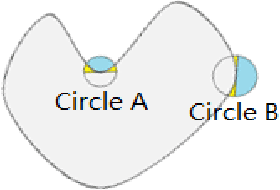
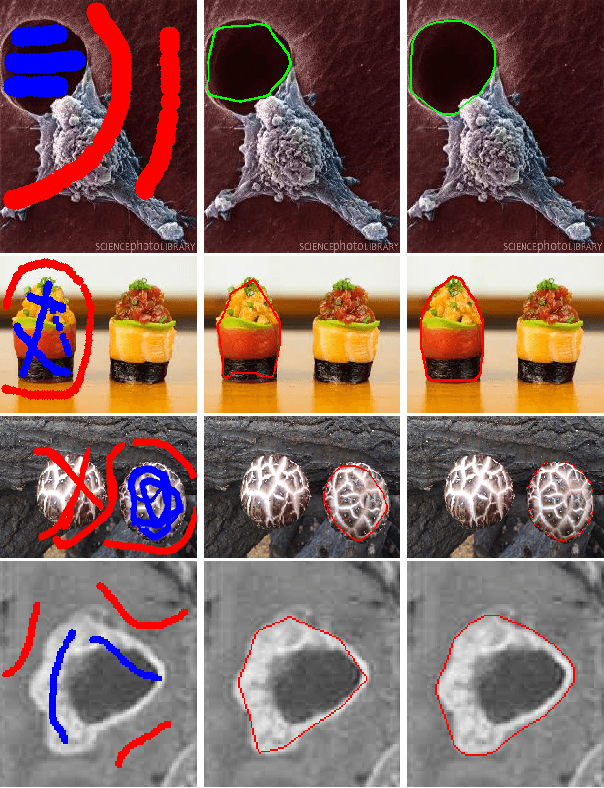
We present a novel and effective binary representation for convex shapes. We show the equivalence between the shape convexity and some properties of the associated indicator function. The proposed method has two advantages. Firstly, the representation is based on a simple inequality constraint on the binary function rather than the definition of convex shapes, which allows us to obtain efficient algorithms for various applications with convexity prior. Secondly, this method is independent of the dimension of the concerned shape. In order to show the effectiveness of the proposed representation approach, we incorporate it with a probability based model for object segmentation with convexity prior. Efficient algorithms are given to solve the proposed models using Lagrange multiplier methods and linear approximations. Various experiments are given to show the superiority of the proposed methods.

Convex hull algorithms based on some variational models

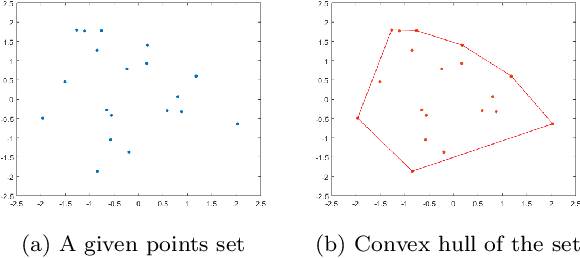
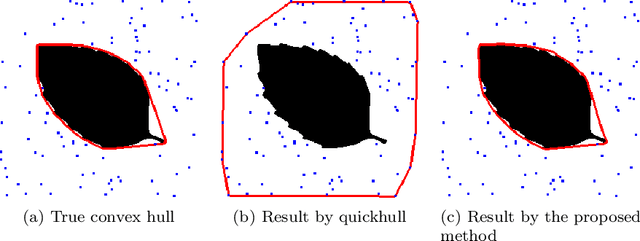
Seeking the convex hull of an object is a very fundamental problem arising from various tasks. In this work, we propose two variational convex hull models using level set representation for 2-dimensional data. The first one is an exact model, which can get the convex hull of one or multiple objects. In this model, the convex hull is characterized by the zero sublevel-set of a convex level set function, which is non-positive at every given point. By minimizing the area of the zero sublevel-set, we can find the desired convex hull. The second one is intended to get convex hull of objects with outliers. Instead of requiring all the given points are included, this model penalizes the distance from each given point to the zero sublevel-set. Literature methods are not able to handle outliers. For the solution of these models, we develop efficient numerical schemes using alternating direction method of multipliers. Numerical examples are given to demonstrate the advantages of the proposed methods.