Multi-Agent Bandit Learning through Heterogeneous Action Erasure Channels

Multi-Armed Bandit (MAB) systems are witnessing an upswing in applications within multi-agent distributed environments, leading to the advancement of collaborative MAB algorithms. In such settings, communication between agents executing actions and the primary learner making decisions can hinder the learning process. A prevalent challenge in distributed learning is action erasure, often induced by communication delays and/or channel noise. This results in agents possibly not receiving the intended action from the learner, subsequently leading to misguided feedback. In this paper, we introduce novel algorithms that enable learners to interact concurrently with distributed agents across heterogeneous action erasure channels with different action erasure probabilities. We illustrate that, in contrast to existing bandit algorithms, which experience linear regret, our algorithms assure sub-linear regret guarantees. Our proposed solutions are founded on a meticulously crafted repetition protocol and scheduling of learning across heterogeneous channels. To our knowledge, these are the first algorithms capable of effectively learning through heterogeneous action erasure channels. We substantiate the superior performance of our algorithm through numerical experiments, emphasizing their practical significance in addressing issues related to communication constraints and delays in multi-agent environments.

Contexts can be Cheap: Solving Stochastic Contextual Bandits with Linear Bandit Algorithms

In this paper, we address the stochastic contextual linear bandit problem, where a decision maker is provided a context (a random set of actions drawn from a distribution). The expected reward of each action is specified by the inner product of the action and an unknown parameter. The goal is to design an algorithm that learns to play as close as possible to the unknown optimal policy after a number of action plays. This problem is considered more challenging than the linear bandit problem, which can be viewed as a contextual bandit problem with a \emph{fixed} context. Surprisingly, in this paper, we show that the stochastic contextual problem can be solved as if it is a linear bandit problem. In particular, we establish a novel reduction framework that converts every stochastic contextual linear bandit instance to a linear bandit instance, when the context distribution is known. When the context distribution is unknown, we establish an algorithm that reduces the stochastic contextual instance to a sequence of linear bandit instances with small misspecifications and achieves nearly the same worst-case regret bound as the algorithm that solves the misspecified linear bandit instances. As a consequence, our results imply a $O(d\sqrt{T\log T})$ high-probability regret bound for contextual linear bandits, making progress in resolving an open problem in (Li et al., 2019), (Li et al., 2021). Our reduction framework opens up a new way to approach stochastic contextual linear bandit problems, and enables improved regret bounds in a number of instances including the batch setting, contextual bandits with misspecifications, contextual bandits with sparse unknown parameters, and contextual bandits with adversarial corruption.

Differentially Private Stochastic Linear Bandits: (Almost) for Free

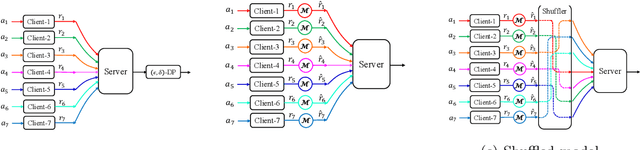
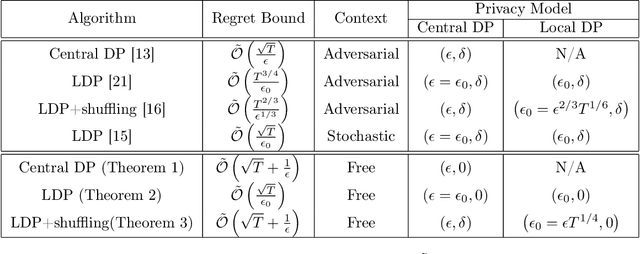
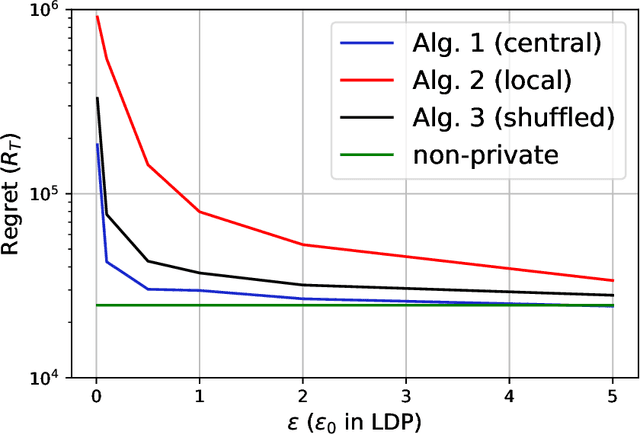
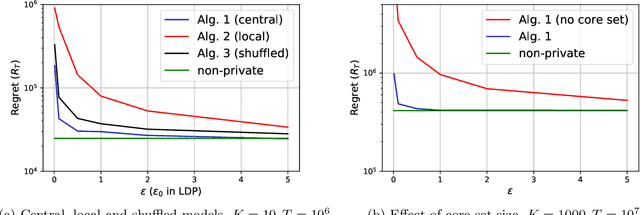
In this paper, we propose differentially private algorithms for the problem of stochastic linear bandits in the central, local and shuffled models. In the central model, we achieve almost the same regret as the optimal non-private algorithms, which means we get privacy for free. In particular, we achieve a regret of $\tilde{O}(\sqrt{T}+\frac{1}{\epsilon})$ matching the known lower bound for private linear bandits, while the best previously known algorithm achieves $\tilde{O}(\frac{1}{\epsilon}\sqrt{T})$. In the local case, we achieve a regret of $\tilde{O}(\frac{1}{\epsilon}{\sqrt{T}})$ which matches the non-private regret for constant $\epsilon$, but suffers a regret penalty when $\epsilon$ is small. In the shuffled model, we also achieve regret of $\tilde{O}(\sqrt{T}+\frac{1}{\epsilon})$ %for small $\epsilon$ as in the central case, while the best previously known algorithm suffers a regret of $\tilde{O}(\frac{1}{\epsilon}{T^{3/5}})$. Our numerical evaluation validates our theoretical results.

Learning in Distributed Contextual Linear Bandits Without Sharing the Context

Contextual linear bandits is a rich and theoretically important model that has many practical applications. Recently, this setup gained a lot of interest in applications over wireless where communication constraints can be a performance bottleneck, especially when the contexts come from a large $d$-dimensional space. In this paper, we consider a distributed memoryless contextual linear bandit learning problem, where the agents who observe the contexts and take actions are geographically separated from the learner who performs the learning while not seeing the contexts. We assume that contexts are generated from a distribution and propose a method that uses $\approx 5d$ bits per context for the case of unknown context distribution and $0$ bits per context if the context distribution is known, while achieving nearly the same regret bound as if the contexts were directly observable. The former bound improves upon existing bounds by a $\log(T)$ factor, where $T$ is the length of the horizon, while the latter achieves information theoretical tightness.

Solving Multi-Arm Bandit Using a Few Bits of Communication

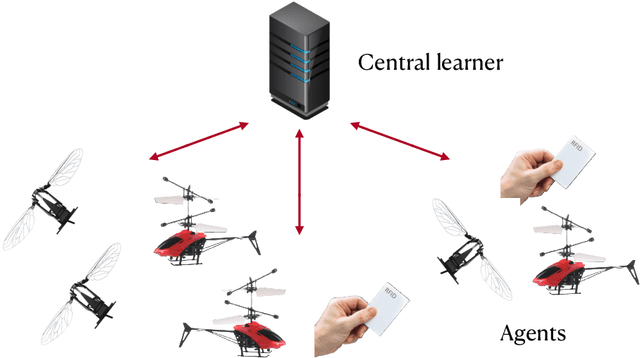
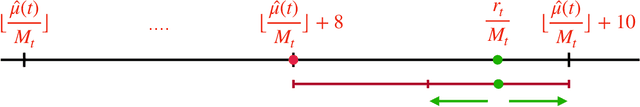
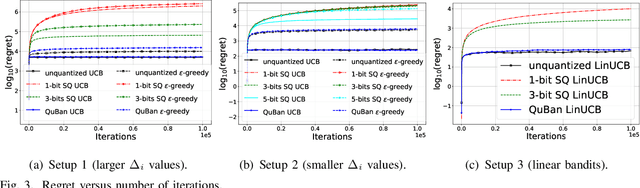
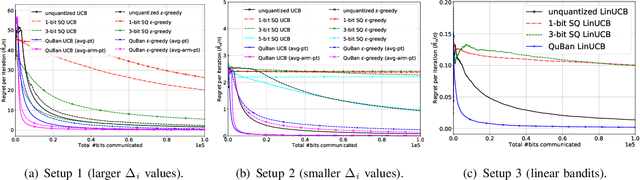
The multi-armed bandit (MAB) problem is an active learning framework that aims to select the best among a set of actions by sequentially observing rewards. Recently, it has become popular for a number of applications over wireless networks, where communication constraints can form a bottleneck. Existing works usually fail to address this issue and can become infeasible in certain applications. In this paper we address the communication problem by optimizing the communication of rewards collected by distributed agents. By providing nearly matching upper and lower bounds, we tightly characterize the number of bits needed per reward for the learner to accurately learn without suffering additional regret. In particular, we establish a generic reward quantization algorithm, QuBan, that can be applied on top of any (no-regret) MAB algorithm to form a new communication-efficient counterpart, that requires only a few (as low as 3) bits to be sent per iteration while preserving the same regret bound. Our lower bound is established via constructing hard instances from a subgaussian distribution. Our theory is further corroborated by numerically experiments.

Quantizing data for distributed learning

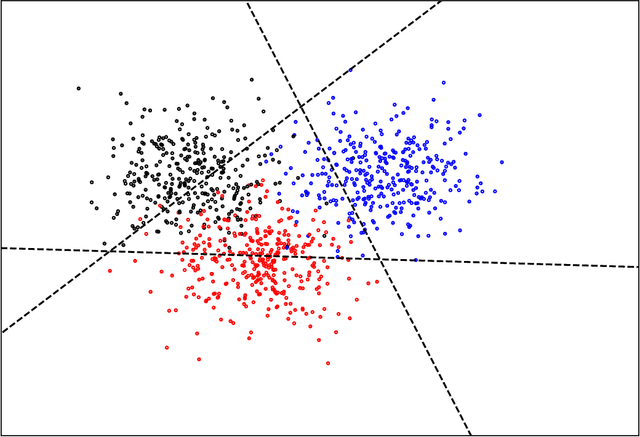
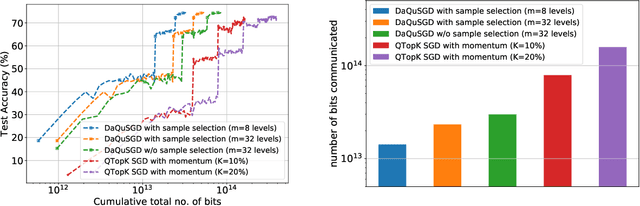
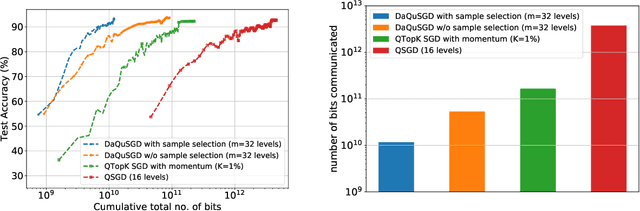
We consider machine learning applications that train a model by leveraging data distributed over a network, where communication constraints can create a performance bottleneck. A number of recent approaches are proposing to overcome this bottleneck through compression of gradient updates. However, as models become larger, so does the size of the gradient updates. In this paper, we propose an alternate approach, that quantizes data instead of gradients, and can support learning over applications where the size of gradient updates is prohibitive. Our approach combines aspects of: (1) sample selection; (2) dataset quantization; and (3) gradient compensation. We analyze the convergence of the proposed approach for smooth convex and non-convex objective functions and show that we can achieve order optimal convergence rates with communication that mostly depends on the data rather than the model (gradient) dimension. We use our proposed algorithm to train ResNet models on the CIFAR-10 and ImageNet datasets, and show that we can achieve an order of magnitude savings over gradient compression methods.

On Distributed Quantization for Classification

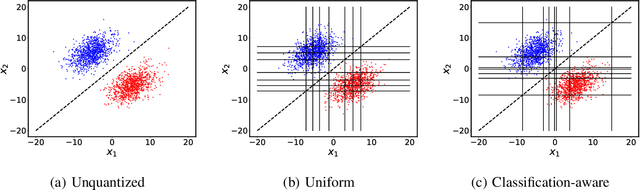
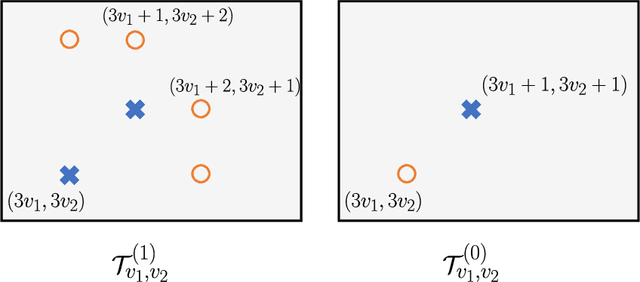
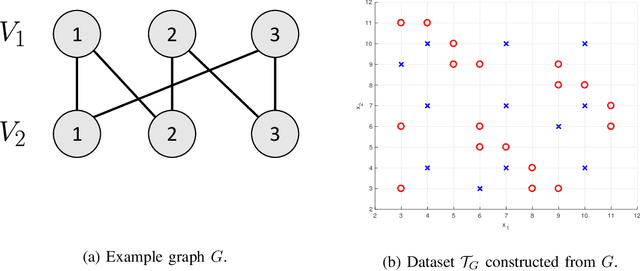
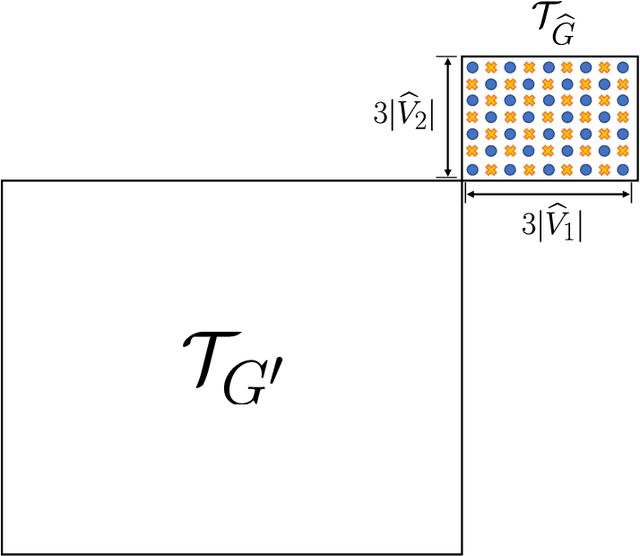
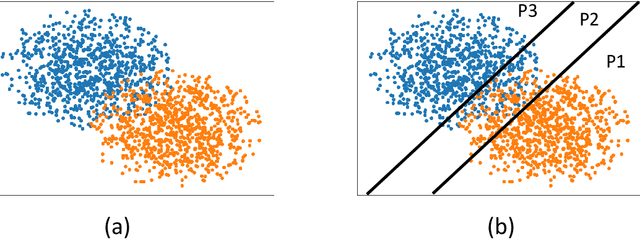
We consider the problem of distributed feature quantization, where the goal is to enable a pretrained classifier at a central node to carry out its classification on features that are gathered from distributed nodes through communication constrained channels. We propose the design of distributed quantization schemes specifically tailored to the classification task: unlike quantization schemes that help the central node reconstruct the original signal as accurately as possible, our focus is not reconstruction accuracy, but instead correct classification. Our work does not make any apriori distributional assumptions on the data, but instead uses training data for the quantizer design. Our main contributions include: we prove NP-hardness of finding optimal quantizers in the general case; we design an optimal scheme for a special case; we propose quantization algorithms, that leverage discrete neural representations and training data, and can be designed in polynomial-time for any number of features, any number of classes, and arbitrary division of features across the distributed nodes. We find that tailoring the quantizers to the classification task can offer significant savings: as compared to alternatives, we can achieve more than a factor of two reduction in terms of the number of bits communicated, for the same classification accuracy.