Optimal Streaming Algorithms for Multi-Armed Bandits

This paper studies two variants of the best arm identification (BAI) problem under the streaming model, where we have a stream of $n$ arms with reward distributions supported on $[0,1]$ with unknown means. The arms in the stream are arriving one by one, and the algorithm cannot access an arm unless it is stored in a limited size memory. We first study the streaming \eps-$top$-$k$ arms identification problem, which asks for $k$ arms whose reward means are lower than that of the $k$-th best arm by at most $\eps$ with probability at least $1-\delta$. For general $\eps \in (0,1)$, the existing solution for this problem assumes $k = 1$ and achieves the optimal sample complexity $O(\frac{n}{\eps^2} \log \frac{1}{\delta})$ using $O(\log^*(n))$ ($\log^*(n)$ equals the number of times that we need to apply the logarithm function on $n$ before the results is no more than 1.) memory and a single pass of the stream. We propose an algorithm that works for any $k$ and achieves the optimal sample complexity $O(\frac{n}{\eps^2} \log\frac{k}{\delta})$ using a single-arm memory and a single pass of the stream. Second, we study the streaming BAI problem, where the objective is to identify the arm with the maximum reward mean with at least $1-\delta$ probability, using a single-arm memory and as few passes of the input stream as possible. We present a single-arm-memory algorithm that achieves a near instance-dependent optimal sample complexity within $O(\log \Delta_2^{-1})$ passes, where $\Delta_2$ is the gap between the mean of the best arm and that of the second best arm.

How Universal Polynomial Bases Enhance Spectral Graph Neural Networks: Heterophily, Over-smoothing, and Over-squashing

Spectral Graph Neural Networks (GNNs), alternatively known as graph filters, have gained increasing prevalence for heterophily graphs. Optimal graph filters rely on Laplacian eigendecomposition for Fourier transform. In an attempt to avert prohibitive computations, numerous polynomial filters have been proposed. However, polynomials in the majority of these filters are predefined and remain fixed across different graphs, failing to accommodate the varying degrees of heterophily. Addressing this gap, we demystify the intrinsic correlation between the spectral property of desired polynomial bases and the heterophily degrees via thorough theoretical analyses. Subsequently, we develop a novel adaptive heterophily basis wherein the basis vectors mutually form angles reflecting the heterophily degree of the graph. We integrate this heterophily basis with the homophily basis to construct a universal polynomial basis UniBasis, which devises a polynomial filter based graph neural network - UniFilter. It optimizes the convolution and propagation in GNN, thus effectively limiting over-smoothing and alleviating over-squashing. Our extensive experiments, conducted on a diverse range of real-world and synthetic datasets with varying degrees of heterophily, support the superiority of UniFilter. These results not only demonstrate the universality of UniBasis but also highlight its proficiency in graph explanation.

Optimizing Polynomial Graph Filters: A Novel Adaptive Krylov Subspace Approach

Graph Neural Networks (GNNs), known as spectral graph filters, find a wide range of applications in web networks. To bypass eigendecomposition, polynomial graph filters are proposed to approximate graph filters by leveraging various polynomial bases for filter training. However, no existing studies have explored the diverse polynomial graph filters from a unified perspective for optimization. In this paper, we first unify polynomial graph filters, as well as the optimal filters of identical degrees into the Krylov subspace of the same order, thus providing equivalent expressive power theoretically. Next, we investigate the asymptotic convergence property of polynomials from the unified Krylov subspace perspective, revealing their limited adaptability in graphs with varying heterophily degrees. Inspired by those facts, we design a novel adaptive Krylov subspace approach to optimize polynomial bases with provable controllability over the graph spectrum so as to adapt various heterophily graphs. Subsequently, we propose AdaptKry, an optimized polynomial graph filter utilizing bases from the adaptive Krylov subspaces. Meanwhile, in light of the diverse spectral properties of complex graphs, we extend AdaptKry by leveraging multiple adaptive Krylov bases without incurring extra training costs. As a consequence, extended AdaptKry is able to capture the intricate characteristics of graphs and provide insights into their inherent complexity. We conduct extensive experiments across a series of real-world datasets. The experimental results demonstrate the superior filtering capability of AdaptKry, as well as the optimized efficacy of the adaptive Krylov basis.

Scalable Continuous-time Diffusion Framework for Network Inference and Influence Estimation

The study of continuous-time information diffusion has been an important area of research for many applications in recent years. When only the diffusion traces (cascades) are accessible, cascade-based network inference and influence estimation are two essential problems to explore. Alas, existing methods exhibit limited capability to infer and process networks with more than a few thousand nodes, suffering from scalability issues. In this paper, we view the diffusion process as a continuous-time dynamical system, based on which we establish a continuous-time diffusion model. Subsequently, we instantiate the model to a scalable and effective framework (FIM) to approximate the diffusion propagation from available cascades, thereby inferring the underlying network structure. Furthermore, we undertake an analysis of the approximation error of FIM for network inference. To achieve the desired scalability for influence estimation, we devise an advanced sampling technique and significantly boost the efficiency. We also quantify the effect of the approximation error on influence estimation theoretically. Experimental results showcase the effectiveness and superior scalability of FIM on network inference and influence estimation.

An Effective Universal Polynomial Basis for Spectral Graph Neural Networks

Spectral Graph Neural Networks (GNNs), also referred to as graph filters have gained increasing prevalence for heterophily graphs. Optimal graph filters rely on Laplacian eigendecomposition for Fourier transform. In an attempt to avert the prohibitive computations, numerous polynomial filters by leveraging distinct polynomials have been proposed to approximate the desired graph filters. However, polynomials in the majority of polynomial filters are predefined and remain fixed across all graphs, failing to accommodate the diverse heterophily degrees across different graphs. To tackle this issue, we first investigate the correlation between polynomial bases of desired graph filters and the degrees of graph heterophily via a thorough theoretical analysis. Afterward, we develop an adaptive heterophily basis by incorporating graph heterophily degrees. Subsequently, we integrate this heterophily basis with the homophily basis, creating a universal polynomial basis UniBasis. In consequence, we devise a general polynomial filter UniFilter. Comprehensive experiments on both real-world and synthetic datasets with varying heterophily degrees significantly support the superiority of UniFilter, demonstrating the effectiveness and generality of UniBasis, as well as its promising capability as a new method for graph analysis.

CAT: Learning to Collaborate Channel and Spatial Attention from Multi-Information Fusion

Channel and spatial attention mechanism has proven to provide an evident performance boost of deep convolution neural networks (CNNs). Most existing methods focus on one or run them parallel (series), neglecting the collaboration between the two attentions. In order to better establish the feature interaction between the two types of attention, we propose a plug-and-play attention module, which we term "CAT"-activating the Collaboration between spatial and channel Attentions based on learned Traits. Specifically, we represent traits as trainable coefficients (i.e., colla-factors) to adaptively combine contributions of different attention modules to fit different image hierarchies and tasks better. Moreover, we propose the global entropy pooling (GEP) apart from global average pooling (GAP) and global maximum pooling (GMP) operators, an effective component in suppressing noise signals by measuring the information disorder of feature maps. We introduce a three-way pooling operation into attention modules and apply the adaptive mechanism to fuse their outcomes. Extensive experiments on MS COCO, Pascal-VOC, Cifar-100, and ImageNet show that our CAT outperforms existing state-of-the-art attention mechanisms in object detection, instance segmentation, and image classification. The model and code will be released soon.

Effective and Scalable Clustering on Massive Attributed Graphs

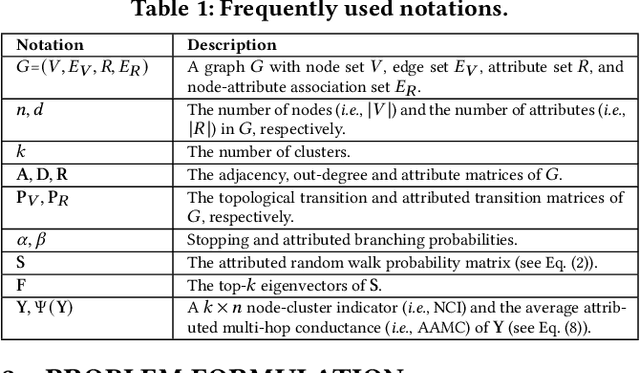
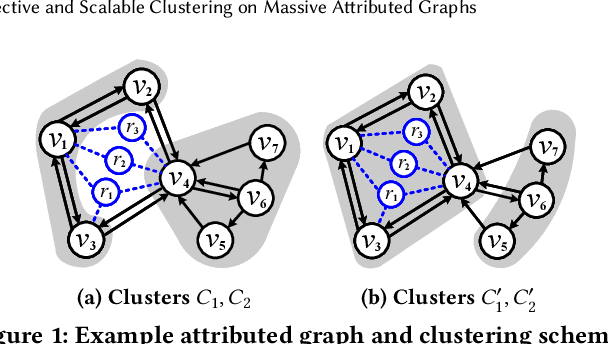
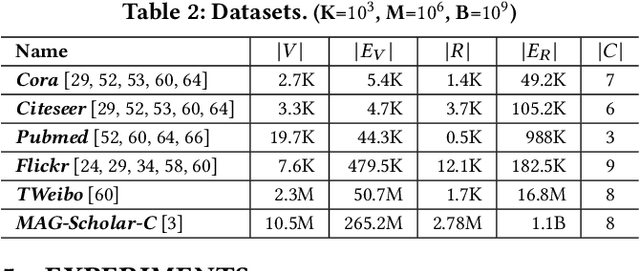
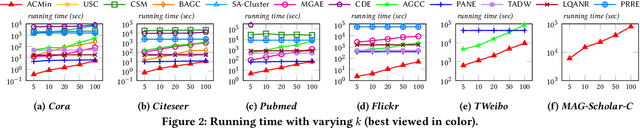
Given a graph G where each node is associated with a set of attributes, and a parameter k specifying the number of output clusters, k-attributed graph clustering (k-AGC) groups nodes in G into k disjoint clusters, such that nodes within the same cluster share similar topological and attribute characteristics, while those in different clusters are dissimilar. This problem is challenging on massive graphs, e.g., with millions of nodes and billions of edges. For such graphs, existing solutions either incur prohibitively high costs, or produce clustering results with compromised quality. In this paper, we propose ACMin, an effective approach to k-AGC that yields high-quality clusters with cost linear to the size of the input graph G. The main contributions of ACMin are twofold: (i) a novel formulation of the k-AGC problem based on an attributed multi-hop conductance quality measure custom-made for this problem setting, which effectively captures cluster coherence in terms of both topological proximities and attribute similarities, and (ii) a linear-time optimization solver that obtains high-quality clusters iteratively, based on efficient matrix operations such as orthogonal iterations, an alternative optimization approach, as well as an initialization technique that significantly speeds up the convergence of ACMin in practice. Extensive experiments, comparing 11 competitors on 6 real datasets, demonstrate that ACMin consistently outperforms all competitors in terms of result quality measured against ground-truth labels, while being up to orders of magnitude faster. In particular, on the Microsoft Academic Knowledge Graph dataset with 265.2 million edges and 1.1 billion attribute values, ACMin outputs high-quality results for 5-AGC within 1.68 hours using a single CPU core, while none of the 11 competitors finish within 3 days.