SplineFlow: Flow Matching for Dynamical Systems with B-Spline Interpolants

Flow matching is a scalable generative framework for characterizing continuous normalizing flows with wide-range applications. However, current state-of-the-art methods are not well-suited for modeling dynamical systems, as they construct conditional paths using linear interpolants that may not capture the underlying state evolution, especially when learning higher-order dynamics from irregular sampled observations. Constructing unified paths that satisfy multi-marginal constraints across observations is challenging, since naïve higher-order polynomials tend to be unstable and oscillatory. We introduce SplineFlow, a theoretically grounded flow matching algorithm that jointly models conditional paths across observations via B-spline interpolation. Specifically, SplineFlow exploits the smoothness and stability of B-spline bases to learn the complex underlying dynamics in a structured manner while ensuring the multi-marginal requirements are met. Comprehensive experiments across various deterministic and stochastic dynamical systems of varying complexity, as well as on cellular trajectory inference tasks, demonstrate the strong improvement of SplineFlow over existing baselines. Our code is available at: https://github.com/santanurathod/SplineFlow.

An Empirical Investigation of Neural ODEs and Symbolic Regression for Dynamical Systems

Accurately modelling the dynamics of complex systems and discovering their governing differential equations are critical tasks for accelerating scientific discovery. Using noisy, synthetic data from two damped oscillatory systems, we explore the extrapolation capabilities of Neural Ordinary Differential Equations (NODEs) and the ability of Symbolic Regression (SR) to recover the underlying equations. Our study yields three key insights. First, we demonstrate that NODEs can extrapolate effectively to new boundary conditions, provided the resulting trajectories share dynamic similarity with the training data. Second, SR successfully recovers the equations from noisy ground-truth data, though its performance is contingent on the correct selection of input variables. Finally, we find that SR recovers two out of the three governing equations, along with a good approximation for the third, when using data generated by a NODE trained on just 10% of the full simulation. While this last finding highlights an area for future work, our results suggest that using NODEs to enrich limited data and enable symbolic regression to infer physical laws represents a promising new approach for scientific discovery.

MixFlow: Mixture-Conditioned Flow Matching for Out-of-Distribution Generalization

Achieving robust generalization under distribution shift remains a central challenge in conditional generative modeling, as existing conditional flow-based methods often struggle to extrapolate beyond the training conditions. We introduce MixFlow, a conditional flow-matching framework for descriptor-controlled generation that directly targets this limitation by jointly learning a descriptor-conditioned base distribution and a descriptor-conditioned flow field via shortest-path flow matching. By modeling the base distribution as a learnable, descriptor-dependent mixture, MixFlow enables smooth interpolation and extrapolation to unseen conditions, leading to substantially improved out-of-distribution generalization. We provide analytical insights into the behavior of the proposed framework and empirically demonstrate its effectiveness across multiple domains, including prediction of responses to unseen perturbations in single-cell transcriptomic data and high-content microscopy-based drug screening tasks. Across these diverse settings, MixFlow consistently outperforms standard conditional flow-matching baselines. Overall, MixFlow offers a simple yet powerful approach for achieving robust, generalizable, and controllable generative modeling across heterogeneous domains.

VLM-CAD: VLM-Optimized Collaborative Agent Design Workflow for Analog Circuit Sizing

Analog mixed-signal circuit sizing involves complex trade-offs within high-dimensional design spaces. Existing automatic analog circuit sizing approaches often underutilize circuit schematics and lack the explainability required for industry adoption. To tackle these challenges, we propose a Vision Language Model-optimized collaborative agent design workflow (VLM-CAD), which analyzes circuits, optimizes DC operating points, performs inference-based sizing and executes external sizing optimization. We integrate Image2Net to annotate circuit schematics and generate a structured JSON description for precise interpretation by Vision Language Models. Furthermore, we propose an Explainable Trust Region Bayesian Optimization method (ExTuRBO) that employs collaborative warm-starting from agent-generated seeds and offers dual-granularity sensitivity analysis for external sizing optimization, supporting a comprehensive final design report. Experiment results on amplifier sizing tasks using 180nm, 90nm, and 45nm Predictive Technology Models demonstrate that VLM-CAD effectively balances power and performance, achieving a 100% success rate in optimizing an amplifier with a complementary input and a class-AB output stage, while maintaining total runtime under 43 minutes across all experiments.

When Numbers Start Talking: Implicit Numerical Coordination Among LLM-Based Agents

LLMs-based agents increasingly operate in multi-agent environments where strategic interaction and coordination are required. While existing work has largely focused on individual agents or on interacting agents sharing explicit communication, less is known about how interacting agents coordinate implicitly. In particular, agents may engage in covert communication, relying on indirect or non-linguistic signals embedded in their actions rather than on explicit messages. This paper presents a game-theoretic study of covert communication in LLM-driven multi-agent systems. We analyse interactions across four canonical game-theoretic settings under different communication regimes, including explicit, restricted, and absent communication. Considering heterogeneous agent personalities and both one-shot and repeated games, we characterise when covert signals emerge and how they shape coordination and strategic outcomes.

An AI Monkey Gets Grapes for Sure -- Sphere Neural Networks for Reliable Decision-Making

This paper compares three methodological categories of neural reasoning: LLM reasoning, supervised learning-based reasoning, and explicit model-based reasoning. LLMs remain unreliable and struggle with simple decision-making that animals can master without extensive corpora training. Through disjunctive syllogistic reasoning testing, we show that reasoning via supervised learning is less appealing than reasoning via explicit model construction. Concretely, we show that an Euler Net trained to achieve 100.00% in classic syllogistic reasoning can be trained to reach 100.00% accuracy in disjunctive syllogistic reasoning. However, the retrained Euler Net suffers severely from catastrophic forgetting (its performance drops to 6.25% on already-learned classic syllogistic reasoning), and its reasoning competence is limited to the pattern level. We propose a new version of Sphere Neural Networks that embeds concepts as circles on the surface of an n-dimensional sphere. These Sphere Neural Networks enable the representation of the negation operator via complement circles and achieve reliable decision-making by filtering out illogical statements that form unsatisfiable circular configurations. We demonstrate that the Sphere Neural Network can master 16 syllogistic reasoning tasks, including rigorous disjunctive syllogistic reasoning, while preserving the rigour of classical syllogistic reasoning. We conclude that neural reasoning with explicit model construction is the most reliable among the three methodological categories of neural reasoning.

How Smoothing is N-simplicial Attention?

Going from pure Multilayer Perceptron (MLP) to a learnable graph message-passing mechanism at each layer has been foundational to state-of-the-art results, despite the computational trade-off (e.g. GATs or Transformers). To go a step further, in this work, we introduce N-simplicial attention, going from pairwise token similarity to higher-order interactions, and adapt it for Rotary Position Embeddings (RoPE). To help manage the increased complexity, we propose a cost-effective simplex selection enabling the model to focus its computation load onto the more task-sensitive interactions. Beyond these core mechanisms, we study how smoothing N-simplicial attention is by deriving a Lipschitz upper-bound and by demonstrating that by itself it also suffers from over-smoothing, despite opening the attention message-passing to higher-order interactions.

MoRE-GNN: Multi-omics Data Integration with a Heterogeneous Graph Autoencoder

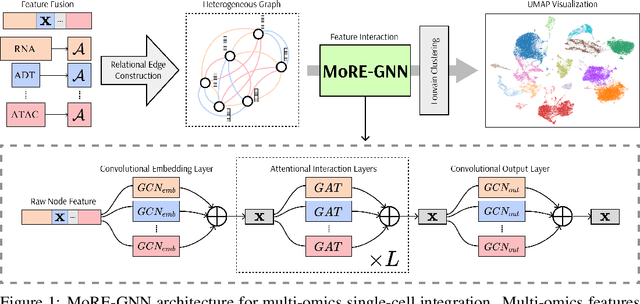
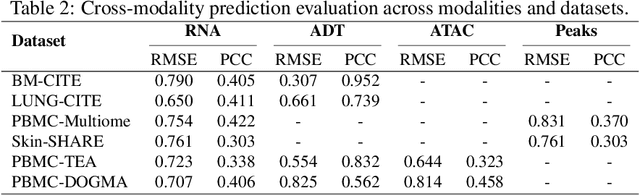
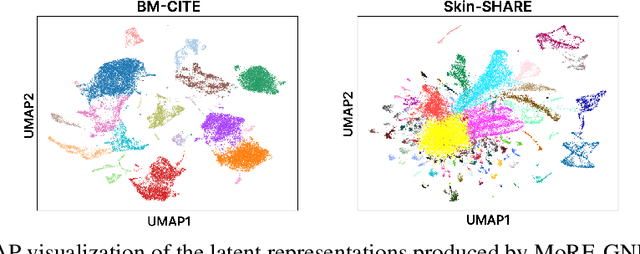
The integration of multi-omics single-cell data remains challenging due to high-dimensionality and complex inter-modality relationships. To address this, we introduce MoRE-GNN (Multi-omics Relational Edge Graph Neural Network), a heterogeneous graph autoencoder that combines graph convolution and attention mechanisms to dynamically construct relational graphs directly from data. Evaluations on six publicly available datasets demonstrate that MoRE-GNN captures biologically meaningful relationships and outperforms existing methods, particularly in settings with strong inter-modality correlations. Furthermore, the learned representations allow for accurate downstream cross-modal predictions. While performance may vary with dataset complexity, MoRE-GNN offers an adaptive, scalable and interpretable framework for advancing multi-omics integration.

Topotein: Topological Deep Learning for Protein Representation Learning

Protein representation learning (PRL) is crucial for understanding structure-function relationships, yet current sequence- and graph-based methods fail to capture the hierarchical organization inherent in protein structures. We introduce Topotein, a comprehensive framework that applies topological deep learning to PRL through the novel Protein Combinatorial Complex (PCC) and Topology-Complete Perceptron Network (TCPNet). Our PCC represents proteins at multiple hierarchical levels -- from residues to secondary structures to complete proteins -- while preserving geometric information at each level. TCPNet employs SE(3)-equivariant message passing across these hierarchical structures, enabling more effective capture of multi-scale structural patterns. Through extensive experiments on four PRL tasks, TCPNet consistently outperforms state-of-the-art geometric graph neural networks. Our approach demonstrates particular strength in tasks such as fold classification which require understanding of secondary structure arrangements, validating the importance of hierarchical topological features for protein analysis.

How to make Medical AI Systems safer? Simulating Vulnerabilities, and Threats in Multimodal Medical RAG System

Large Vision-Language Models (LVLMs) augmented with Retrieval-Augmented Generation (RAG) are increasingly employed in medical AI to enhance factual grounding through external clinical image-text retrieval. However, this reliance creates a significant attack surface. We propose MedThreatRAG, a novel multimodal poisoning framework that systematically probes vulnerabilities in medical RAG systems by injecting adversarial image-text pairs. A key innovation of our approach is the construction of a simulated semi-open attack environment, mimicking real-world medical systems that permit periodic knowledge base updates via user or pipeline contributions. Within this setting, we introduce and emphasize Cross-Modal Conflict Injection (CMCI), which embeds subtle semantic contradictions between medical images and their paired reports. These mismatches degrade retrieval and generation by disrupting cross-modal alignment while remaining sufficiently plausible to evade conventional filters. While basic textual and visual attacks are included for completeness, CMCI demonstrates the most severe degradation. Evaluations on IU-Xray and MIMIC-CXR QA tasks show that MedThreatRAG reduces answer F1 scores by up to 27.66% and lowers LLaVA-Med-1.5 F1 rates to as low as 51.36%. Our findings expose fundamental security gaps in clinical RAG systems and highlight the urgent need for threat-aware design and robust multimodal consistency checks. Finally, we conclude with a concise set of guidelines to inform the safe development of future multimodal medical RAG systems.