GPT-4o System Card

GPT-4o is an autoregressive omni model that accepts as input any combination of text, audio, image, and video, and generates any combination of text, audio, and image outputs. It's trained end-to-end across text, vision, and audio, meaning all inputs and outputs are processed by the same neural network. GPT-4o can respond to audio inputs in as little as 232 milliseconds, with an average of 320 milliseconds, which is similar to human response time in conversation. It matches GPT-4 Turbo performance on text in English and code, with significant improvement on text in non-English languages, while also being much faster and 50\% cheaper in the API. GPT-4o is especially better at vision and audio understanding compared to existing models. In line with our commitment to building AI safely and consistent with our voluntary commitments to the White House, we are sharing the GPT-4o System Card, which includes our Preparedness Framework evaluations. In this System Card, we provide a detailed look at GPT-4o's capabilities, limitations, and safety evaluations across multiple categories, focusing on speech-to-speech while also evaluating text and image capabilities, and measures we've implemented to ensure the model is safe and aligned. We also include third-party assessments on dangerous capabilities, as well as discussion of potential societal impacts of GPT-4o's text and vision capabilities.

Learning correspondences of cardiac motion from images using biomechanics-informed modeling

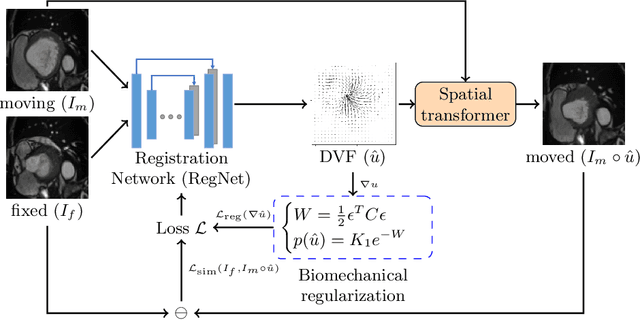
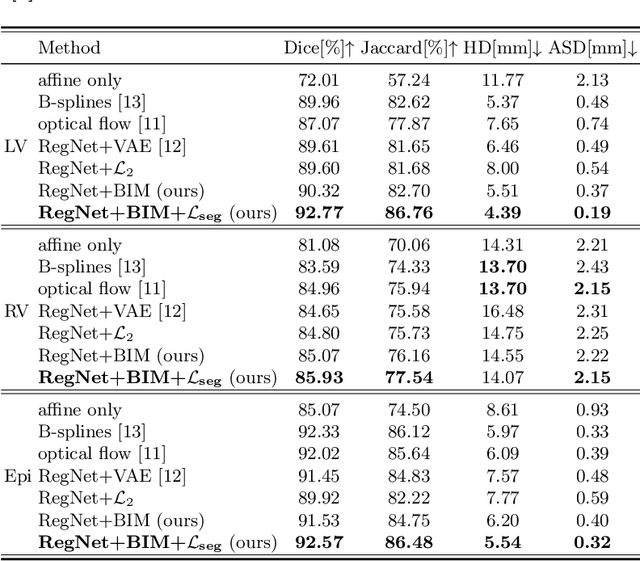
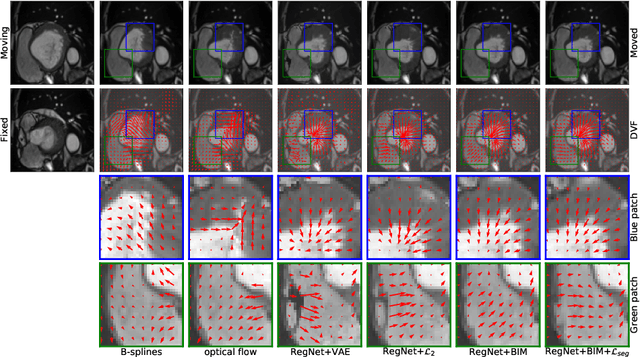
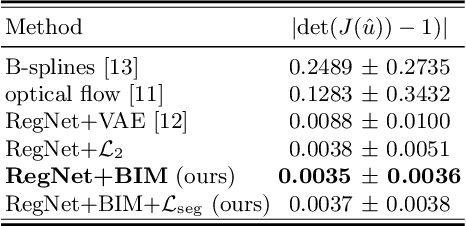
Learning spatial-temporal correspondences in cardiac motion from images is important for understanding the underlying dynamics of cardiac anatomical structures. Many methods explicitly impose smoothness constraints such as the $\mathcal{L}_2$ norm on the displacement vector field (DVF), while usually ignoring biomechanical feasibility in the transformation. Other geometric constraints either regularize specific regions of interest such as imposing incompressibility on the myocardium or introduce additional steps such as training a separate network-based regularizer on physically simulated datasets. In this work, we propose an explicit biomechanics-informed prior as regularization on the predicted DVF in modeling a more generic biomechanically plausible transformation within all cardiac structures without introducing additional training complexity. We validate our methods on two publicly available datasets in the context of 2D MRI data and perform extensive experiments to illustrate the effectiveness and robustness of our proposed methods compared to other competing regularization schemes. Our proposed methods better preserve biomechanical properties by visual assessment and show advantages in segmentation performance using quantitative evaluation metrics. The code is publicly available at \url{https://github.com/Voldemort108X/bioinformed_reg}.

Surrogate Gap Minimization Improves Sharpness-Aware Training

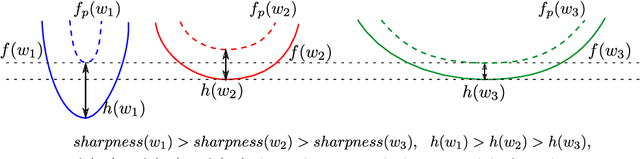
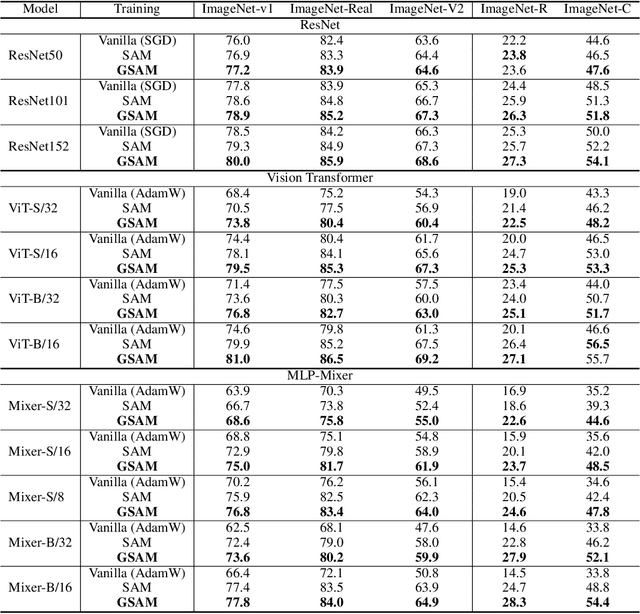
The recently proposed Sharpness-Aware Minimization (SAM) improves generalization by minimizing a \textit{perturbed loss} defined as the maximum loss within a neighborhood in the parameter space. However, we show that both sharp and flat minima can have a low perturbed loss, implying that SAM does not always prefer flat minima. Instead, we define a \textit{surrogate gap}, a measure equivalent to the dominant eigenvalue of Hessian at a local minimum when the radius of the neighborhood (to derive the perturbed loss) is small. The surrogate gap is easy to compute and feasible for direct minimization during training. Based on the above observations, we propose Surrogate \textbf{G}ap Guided \textbf{S}harpness-\textbf{A}ware \textbf{M}inimization (GSAM), a novel improvement over SAM with negligible computation overhead. Conceptually, GSAM consists of two steps: 1) a gradient descent like SAM to minimize the perturbed loss, and 2) an \textit{ascent} step in the \textit{orthogonal} direction (after gradient decomposition) to minimize the surrogate gap and yet not affect the perturbed loss. GSAM seeks a region with both small loss (by step 1) and low sharpness (by step 2), giving rise to a model with high generalization capabilities. Theoretically, we show the convergence of GSAM and provably better generalization than SAM. Empirically, GSAM consistently improves generalization (e.g., +3.2\% over SAM and +5.4\% over AdamW on ImageNet top-1 accuracy for ViT-B/32). Code is released at \url{ https://sites.google.com/view/gsam-iclr22/home}.

Momentum Centering and Asynchronous Update for Adaptive Gradient Methods

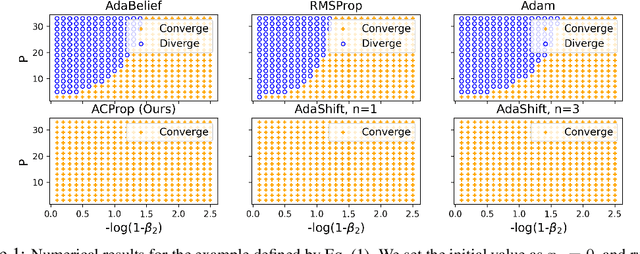
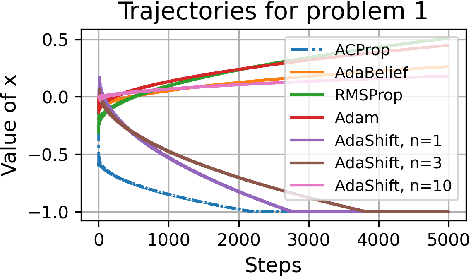
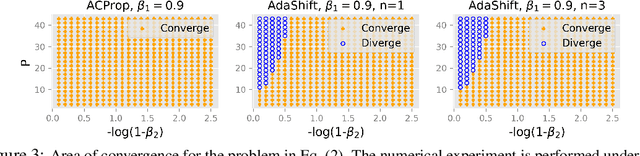
We propose ACProp (Asynchronous-centering-Prop), an adaptive optimizer which combines centering of second momentum and asynchronous update (e.g. for $t$-th update, denominator uses information up to step $t-1$, while numerator uses gradient at $t$-th step). ACProp has both strong theoretical properties and empirical performance. With the example by Reddi et al. (2018), we show that asynchronous optimizers (e.g. AdaShift, ACProp) have weaker convergence condition than synchronous optimizers (e.g. Adam, RMSProp, AdaBelief); within asynchronous optimizers, we show that centering of second momentum further weakens the convergence condition. We demonstrate that ACProp has a convergence rate of $O(\frac{1}{\sqrt{T}})$ for the stochastic non-convex case, which matches the oracle rate and outperforms the $O(\frac{logT}{\sqrt{T}})$ rate of RMSProp and Adam. We validate ACProp in extensive empirical studies: ACProp outperforms both SGD and other adaptive optimizers in image classification with CNN, and outperforms well-tuned adaptive optimizers in the training of various GAN models, reinforcement learning and transformers. To sum up, ACProp has good theoretical properties including weak convergence condition and optimal convergence rate, and strong empirical performance including good generalization like SGD and training stability like Adam. We provide the implementation at https://github.com/juntang-zhuang/ACProp-Optimizer.

Demographic-Guided Attention in Recurrent Neural Networks for Modeling Neuropathophysiological Heterogeneity

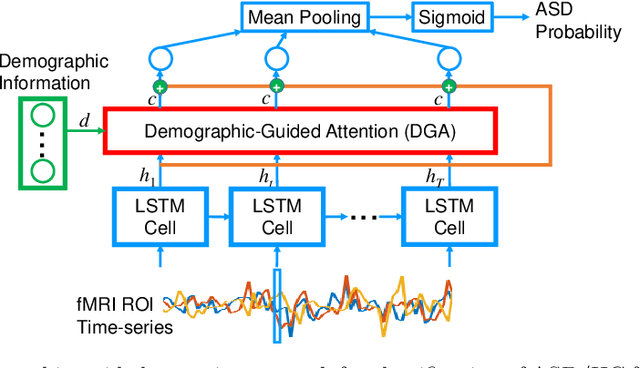
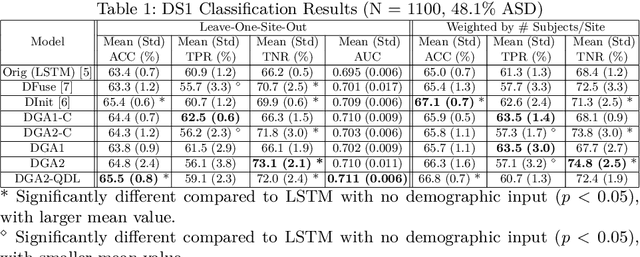
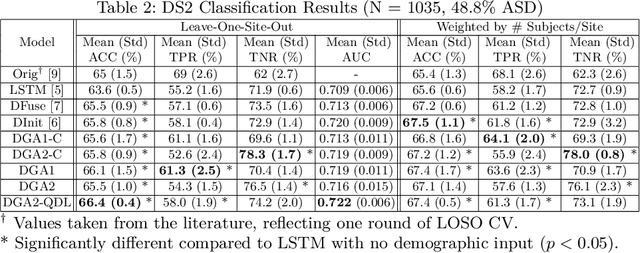
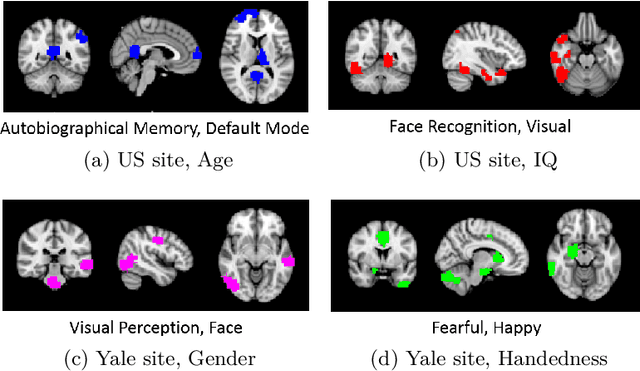
Heterogeneous presentation of a neurological disorder suggests potential differences in the underlying pathophysiological changes that occur in the brain. We propose to model heterogeneous patterns of functional network differences using a demographic-guided attention (DGA) mechanism for recurrent neural network models for prediction from functional magnetic resonance imaging (fMRI) time-series data. The context computed from the DGA head is used to help focus on the appropriate functional networks based on individual demographic information. We demonstrate improved classification on 3 subsets of the ABIDE I dataset used in published studies that have previously produced state-of-the-art results, evaluating performance under a leave-one-site-out cross-validation framework for better generalizeability to new data. Finally, we provide examples of interpreting functional network differences based on individual demographic variables.

MALI: A memory efficient and reverse accurate integrator for Neural ODEs

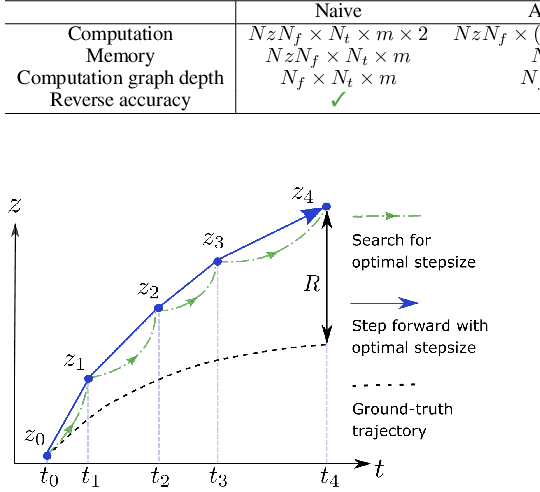
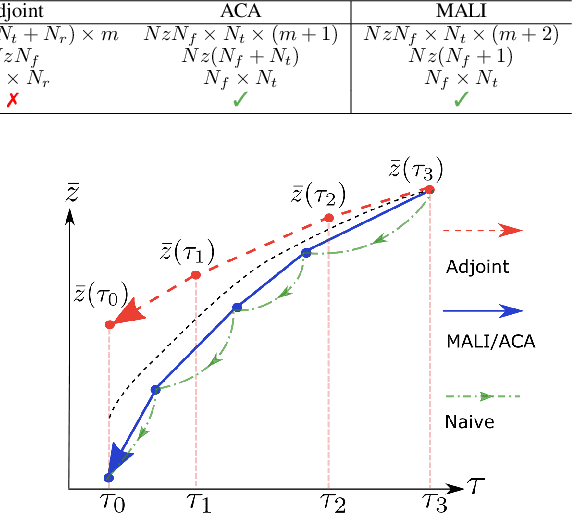
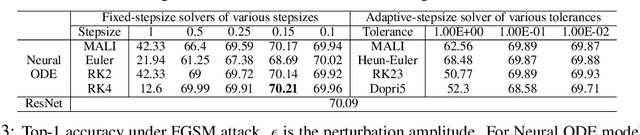
Neural ordinary differential equations (Neural ODEs) are a new family of deep-learning models with continuous depth. However, the numerical estimation of the gradient in the continuous case is not well solved: existing implementations of the adjoint method suffer from inaccuracy in reverse-time trajectory, while the naive method and the adaptive checkpoint adjoint method (ACA) have a memory cost that grows with integration time. In this project, based on the asynchronous leapfrog (ALF) solver, we propose the Memory-efficient ALF Integrator (MALI), which has a constant memory cost \textit{w.r.t} number of solver steps in integration similar to the adjoint method, and guarantees accuracy in reverse-time trajectory (hence accuracy in gradient estimation). We validate MALI in various tasks: on image recognition tasks, to our knowledge, MALI is the first to enable feasible training of a Neural ODE on ImageNet and outperform a well-tuned ResNet, while existing methods fail due to either heavy memory burden or inaccuracy; for time series modeling, MALI significantly outperforms the adjoint method; and for continuous generative models, MALI achieves new state-of-the-art performance. We provide a pypi package at \url{https://jzkay12.github.io/TorchDiffEqPack/}

Multiple-shooting adjoint method for whole-brain dynamic causal modeling

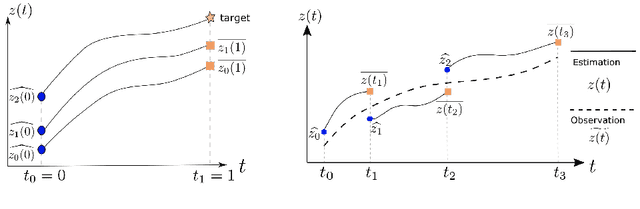
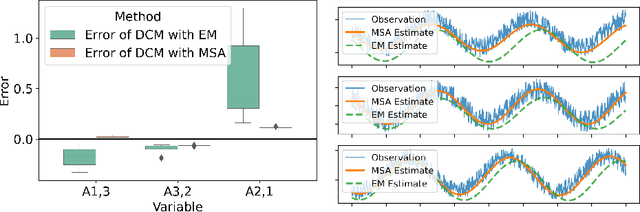
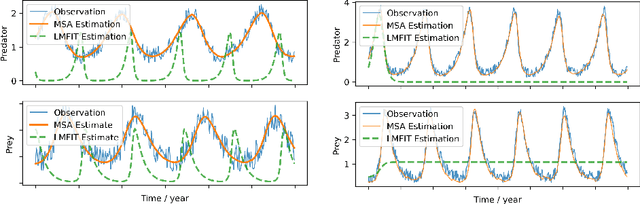
Dynamic causal modeling (DCM) is a Bayesian framework to infer directed connections between compartments, and has been used to describe the interactions between underlying neural populations based on functional neuroimaging data. DCM is typically analyzed with the expectation-maximization (EM) algorithm. However, because the inversion of a large-scale continuous system is difficult when noisy observations are present, DCM by EM is typically limited to a small number of compartments ($<10$). Another drawback with the current method is its complexity; when the forward model changes, the posterior mean changes, and we need to re-derive the algorithm for optimization. In this project, we propose the Multiple-Shooting Adjoint (MSA) method to address these limitations. MSA uses the multiple-shooting method for parameter estimation in ordinary differential equations (ODEs) under noisy observations, and is suitable for large-scale systems such as whole-brain analysis in functional MRI (fMRI). Furthermore, MSA uses the adjoint method for accurate gradient estimation in the ODE; since the adjoint method is generic, MSA is a generic method for both linear and non-linear systems, and does not require re-derivation of the algorithm as in EM. We validate MSA in extensive experiments: 1) in toy examples with both linear and non-linear models, we show that MSA achieves better accuracy in parameter value estimation than EM; furthermore, MSA can be successfully applied to large systems with up to 100 compartments; and 2) using real fMRI data, we apply MSA to the estimation of the whole-brain effective connectome and show improved classification of autism spectrum disorder (ASD) vs. control compared to using the functional connectome. The package is provided \url{https://jzkay12.github.io/TorchDiffEqPack}

AdaBelief Optimizer: Adapting Stepsizes by the Belief in Observed Gradients

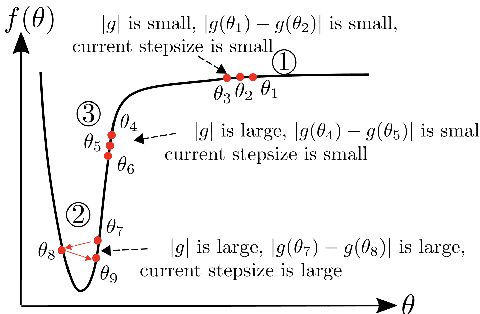
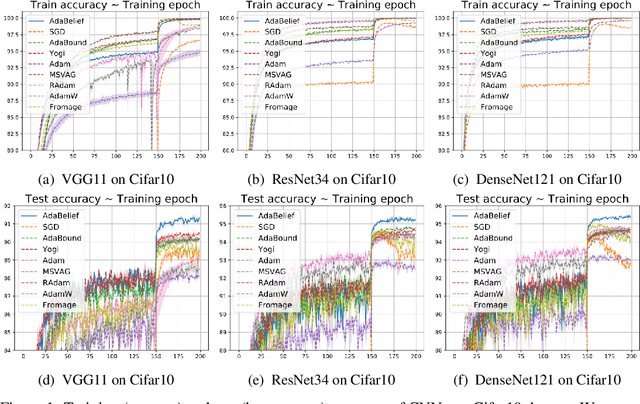
Most popular optimizers for deep learning can be broadly categorized as adaptive methods (e.g. Adam) and accelerated schemes (e.g. stochastic gradient descent (SGD) with momentum). For many models such as convolutional neural networks (CNNs), adaptive methods typically converge faster but generalize worse compared to SGD; for complex settings such as generative adversarial networks (GANs), adaptive methods are typically the default because of their stability.We propose AdaBelief to simultaneously achieve three goals: fast convergence as in adaptive methods, good generalization as in SGD, and training stability. The intuition for AdaBelief is to adapt the stepsize according to the "belief" in the current gradient direction. Viewing the exponential moving average (EMA) of the noisy gradient as the prediction of the gradient at the next time step, if the observed gradient greatly deviates from the prediction, we distrust the current observation and take a small step; if the observed gradient is close to the prediction, we trust it and take a large step. We validate AdaBelief in extensive experiments, showing that it outperforms other methods with fast convergence and high accuracy on image classification and language modeling. Specifically, on ImageNet, AdaBelief achieves comparable accuracy to SGD. Furthermore, in the training of a GAN on Cifar10, AdaBelief demonstrates high stability and improves the quality of generated samples compared to a well-tuned Adam optimizer. Code is available at https://github.com/juntang-zhuang/Adabelief-Optimizer

Pooling Regularized Graph Neural Network for fMRI Biomarker Analysis

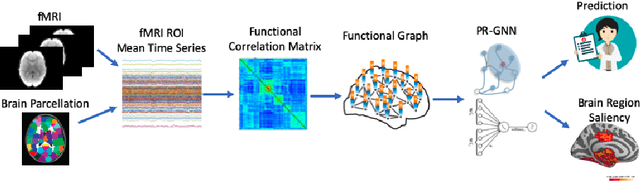
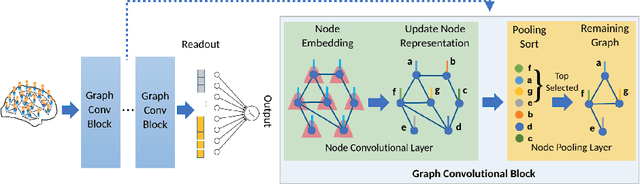
Understanding how certain brain regions relate to a specific neurological disorder has been an important area of neuroimaging research. A promising approach to identify the salient regions is using Graph Neural Networks (GNNs), which can be used to analyze graph structured data, e.g. brain networks constructed by functional magnetic resonance imaging (fMRI). We propose an interpretable GNN framework with a novel salient region selection mechanism to determine neurological brain biomarkers associated with disorders. Specifically, we design novel regularized pooling layers that highlight salient regions of interests (ROIs) so that we can infer which ROIs are important to identify a certain disease based on the node pooling scores calculated by the pooling layers. Our proposed framework, Pooling Regularized-GNN (PR-GNN), encourages reasonable ROI-selection and provides flexibility to preserve either individual- or group-level patterns. We apply the PR-GNN framework on a Biopoint Autism Spectral Disorder (ASD) fMRI dataset. We investigate different choices of the hyperparameters and show that PR-GNN outperforms baseline methods in terms of classification accuracy. The salient ROI detection results show high correspondence with the previous neuroimaging-derived biomarkers for ASD.

Neuropsychiatric Disease Classification Using Functional Connectomics -- Results of the Connectomics in NeuroImaging Transfer Learning Challenge

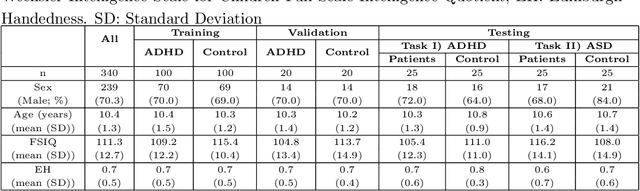
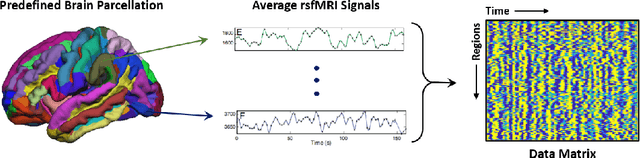
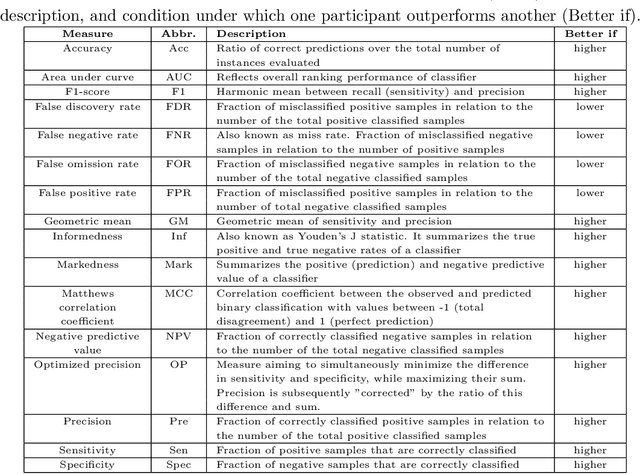
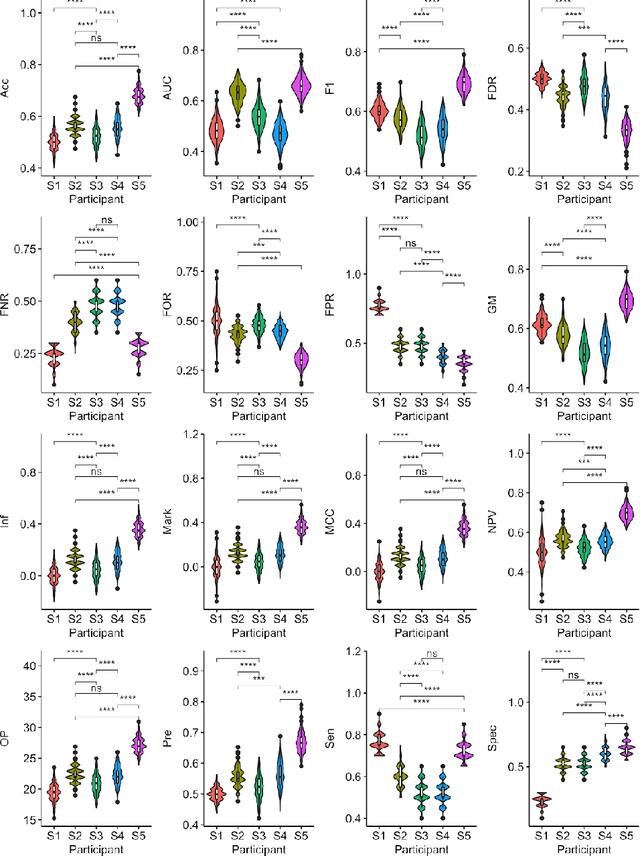
Large, open-source consortium datasets have spurred the development of new and increasingly powerful machine learning approaches in brain connectomics. However, one key question remains: are we capturing biologically relevant and generalizable information about the brain, or are we simply overfitting to the data? To answer this, we organized a scientific challenge, the Connectomics in NeuroImaging Transfer Learning Challenge (CNI-TLC), held in conjunction with MICCAI 2019. CNI-TLC included two classification tasks: (1) diagnosis of Attention-Deficit/Hyperactivity Disorder (ADHD) within a pre-adolescent cohort; and (2) transference of the ADHD model to a related cohort of Autism Spectrum Disorder (ASD) patients with an ADHD comorbidity. In total, 240 resting-state fMRI time series averaged according to three standard parcellation atlases, along with clinical diagnosis, were released for training and validation (120 neurotypical controls and 120 ADHD). We also provided demographic information of age, sex, IQ, and handedness. A second set of 100 subjects (50 neurotypical controls, 25 ADHD, and 25 ASD with ADHD comorbidity) was used for testing. Models were submitted in a standardized format as Docker images through ChRIS, an open-source image analysis platform. Utilizing an inclusive approach, we ranked the methods based on 16 different metrics. The final rank was calculated using the rank product for each participant across all measures. Furthermore, we assessed the calibration curves of each method. Five participants submitted their model for evaluation, with one outperforming all other methods in both ADHD and ASD classification. However, further improvements are needed to reach the clinical translation of functional connectomics. We are keeping the CNI-TLC open as a publicly available resource for developing and validating new classification methodologies in the field of connectomics.