John Lafferty
University of Chicago
Model Repair: Robust Recovery of Over-Parameterized Statistical Models
May 20, 2020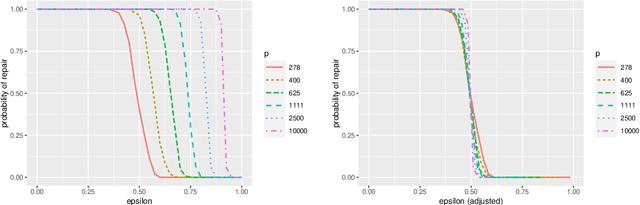
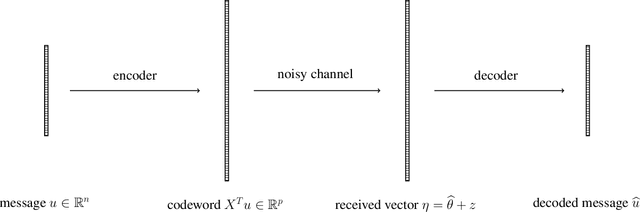
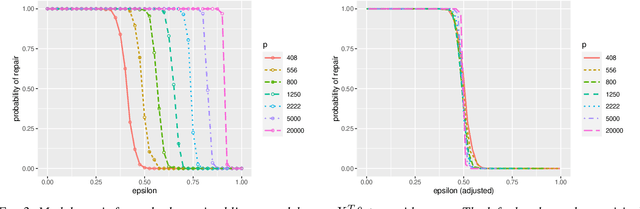
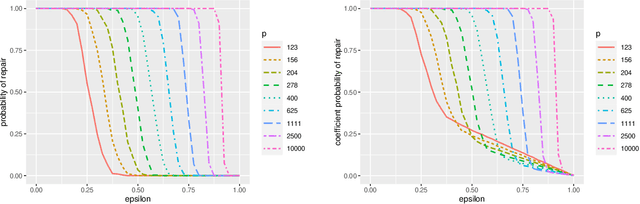
Abstract:A new type of robust estimation problem is introduced where the goal is to recover a statistical model that has been corrupted after it has been estimated from data. Methods are proposed for "repairing" the model using only the design and not the response values used to fit the model in a supervised learning setting. Theory is developed which reveals that two important ingredients are necessary for model repair---the statistical model must be over-parameterized, and the estimator must incorporate redundancy. In particular, estimators based on stochastic gradient descent are seen to be well suited to model repair, but sparse estimators are not in general repairable. After formulating the problem and establishing a key technical lemma related to robust estimation, a series of results are presented for repair of over-parameterized linear models, random feature models, and artificial neural networks. Simulation studies are presented that corroborate and illustrate the theoretical findings.
Surfing: Iterative optimization over incrementally trained deep networks
Jul 19, 2019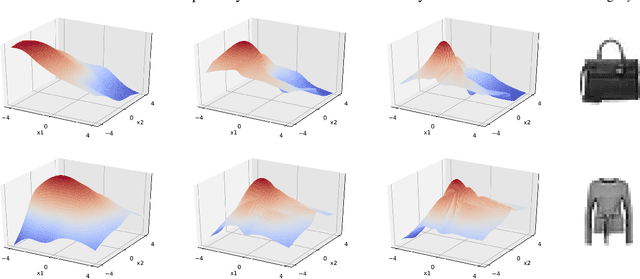
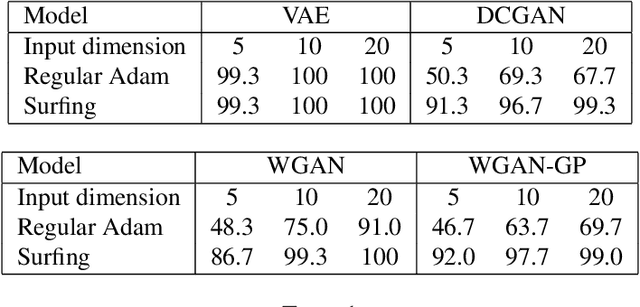
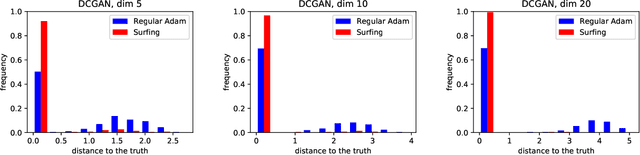
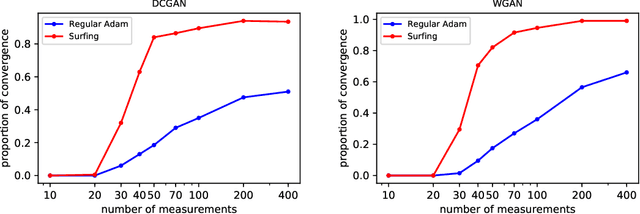
Abstract:We investigate a sequential optimization procedure to minimize the empirical risk functional $f_{\hat\theta}(x) = \frac{1}{2}\|G_{\hat\theta}(x) - y\|^2$ for certain families of deep networks $G_{\theta}(x)$. The approach is to optimize a sequence of objective functions that use network parameters obtained during different stages of the training process. When initialized with random parameters $\theta_0$, we show that the objective $f_{\theta_0}(x)$ is "nice'' and easy to optimize with gradient descent. As learning is carried out, we obtain a sequence of generative networks $x \mapsto G_{\theta_t}(x)$ and associated risk functions $f_{\theta_t}(x)$, where $t$ indicates a stage of stochastic gradient descent during training. Since the parameters of the network do not change by very much in each step, the surface evolves slowly and can be incrementally optimized. The algorithm is formalized and analyzed for a family of expansive networks. We call the procedure {\it surfing} since it rides along the peak of the evolving (negative) empirical risk function, starting from a smooth surface at the beginning of learning and ending with a wavy nonconvex surface after learning is complete. Experiments show how surfing can be used to find the global optimum and for compressed sensing even when direct gradient descent on the final learned network fails.
Fair quantile regression
Jul 19, 2019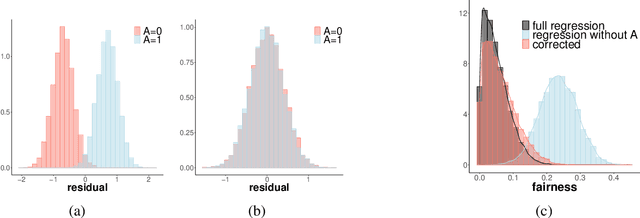
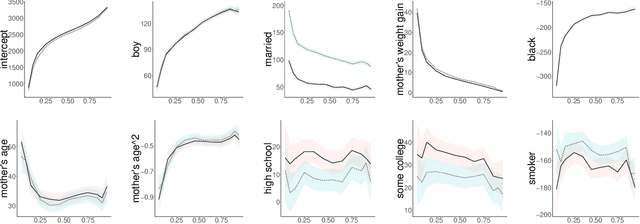
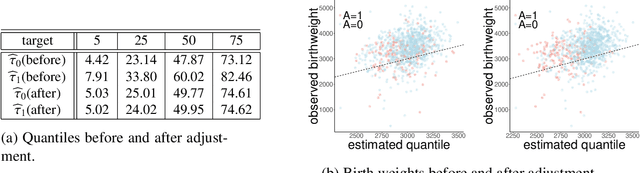
Abstract:Quantile regression is a tool for learning conditional distributions. In this paper we study quantile regression in the setting where a protected attribute is unavailable when fitting the model. This can lead to "unfair'' quantile estimators for which the effective quantiles are very different for the subpopulations defined by the protected attribute. We propose a procedure for adjusting the estimator on a heldout sample where the protected attribute is available. The main result of the paper is an empirical process analysis showing that the adjustment leads to a fair estimator for which the target quantiles are brought into balance, in a statistical sense that we call $\sqrt{n}$-fairness. We illustrate the ideas and adjustment procedure on a dataset of 200,000 live births, where the objective is to characterize the dependence of the birth weights of the babies on demographic attributes of the birth mother; the protected attribute is the mother's race.
TopicEq: A Joint Topic and Mathematical Equation Model for Scientific Texts
Feb 20, 2019
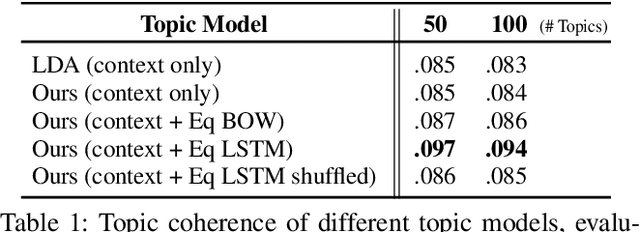
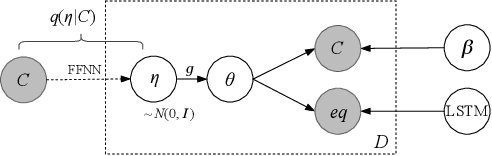

Abstract:Scientific documents rely on both mathematics and text to communicate ideas. Inspired by the topical correspondence between mathematical equations and word contexts observed in scientific texts, we propose a novel topic model that jointly generates mathematical equations and their surrounding text (TopicEq). Using an extension of the correlated topic model, the context is generated from a mixture of latent topics, and the equation is generated by an RNN that depends on the latent topic activations. To experiment with this model, we create a corpus of 400K equation-context pairs extracted from a range of scientific articles from arXiv, and fit the model using a variational autoencoder approach. Experimental results show that this joint model significantly outperforms existing topic models and equation models for scientific texts. Moreover, we qualitatively show that the model effectively captures the relationship between topics and mathematics, enabling novel applications such as topic-aware equation generation, equation topic inference, and topic-aware alignment of mathematical symbols and words.
Distributed Nonparametric Regression under Communication Constraints
Jun 23, 2018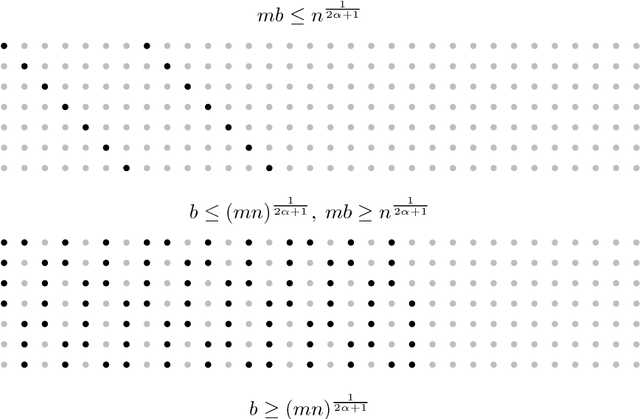
Abstract:This paper studies the problem of nonparametric estimation of a smooth function with data distributed across multiple machines. We assume an independent sample from a white noise model is collected at each machine, and an estimator of the underlying true function needs to be constructed at a central machine. We place limits on the number of bits that each machine can use to transmit information to the central machine. Our results give both asymptotic lower bounds and matching upper bounds on the statistical risk under various settings. We identify three regimes, depending on the relationship among the number of machines, the size of the data available at each machine, and the communication budget. When the communication budget is small, the statistical risk depends solely on this communication bottleneck, regardless of the sample size. In the regime where the communication budget is large, the classic minimax risk in the non-distributed estimation setting is recovered. In an intermediate regime, the statistical risk depends on both the sample size and the communication budget.
Prediction Rule Reshaping
May 16, 2018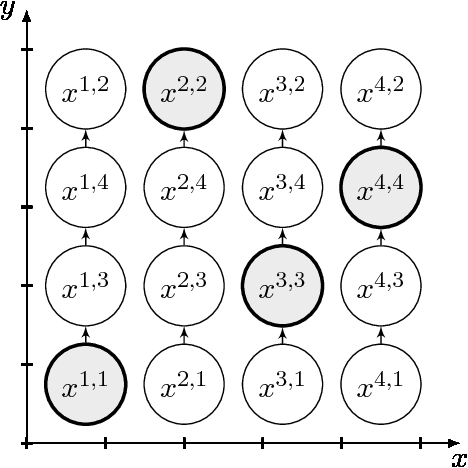

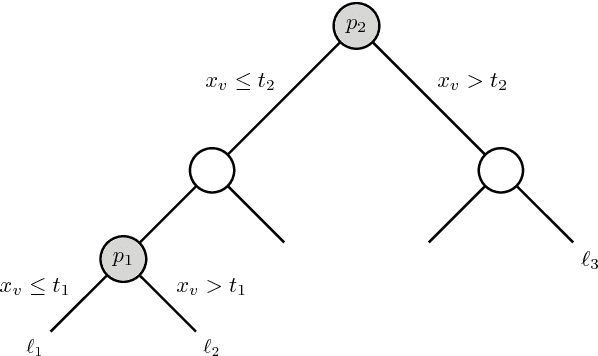

Abstract:Two methods are proposed for high-dimensional shape-constrained regression and classification. These methods reshape pre-trained prediction rules to satisfy shape constraints like monotonicity and convexity. The first method can be applied to any pre-trained prediction rule, while the second method deals specifically with random forests. In both cases, efficient algorithms are developed for computing the estimators, and experiments are performed to demonstrate their performance on four datasets. We find that reshaping methods enforce shape constraints without compromising predictive accuracy.
Quantized Nonparametric Estimation over Sobolev Ellipsoids
Apr 11, 2017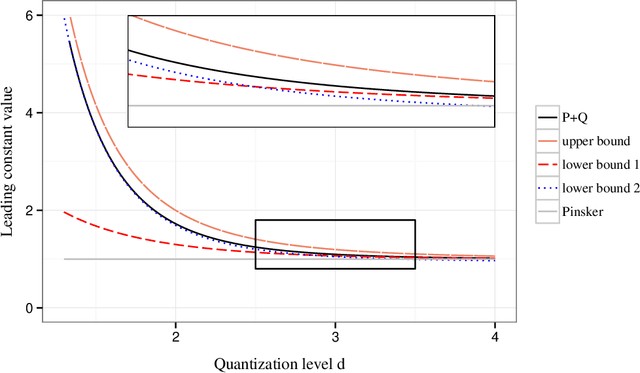
Abstract:We formulate the notion of minimax estimation under storage or communication constraints, and prove an extension to Pinsker's theorem for nonparametric estimation over Sobolev ellipsoids. Placing limits on the number of bits used to encode any estimator, we give tight lower and upper bounds on the excess risk due to quantization in terms of the number of bits, the signal size, and the noise level. This establishes the Pareto optimal tradeoff between storage and risk under quantization constraints for Sobolev spaces. Our results and proof techniques combine elements of rate distortion theory and minimax analysis. The proposed quantized estimation scheme, which shows achievability of the lower bounds, is adaptive in the usual statistical sense, achieving the optimal quantized minimax rate without knowledge of the smoothness parameter of the Sobolev space. It is also adaptive in a computational sense, as it constructs the code only after observing the data, to dynamically allocate more codewords to blocks where the estimated signal size is large. Simulations are included that illustrate the effect of quantization on statistical risk.
Convergence Analysis for Rectangular Matrix Completion Using Burer-Monteiro Factorization and Gradient Descent
Nov 22, 2016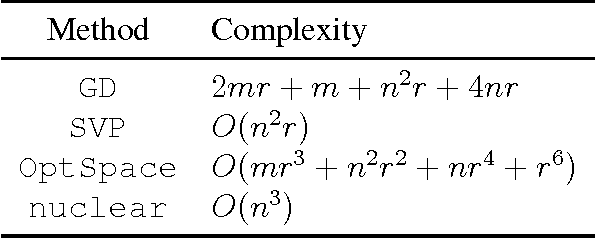
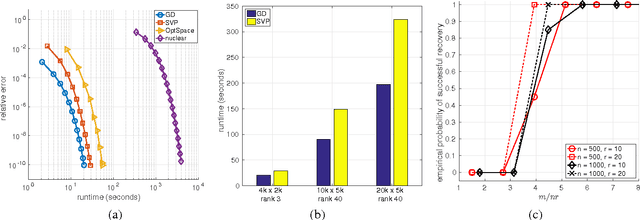
Abstract:We address the rectangular matrix completion problem by lifting the unknown matrix to a positive semidefinite matrix in higher dimension, and optimizing a nonconvex objective over the semidefinite factor using a simple gradient descent scheme. With $O( \mu r^2 \kappa^2 n \max(\mu, \log n))$ random observations of a $n_1 \times n_2$ $\mu$-incoherent matrix of rank $r$ and condition number $\kappa$, where $n = \max(n_1, n_2)$, the algorithm linearly converges to the global optimum with high probability.
Local Minimax Complexity of Stochastic Convex Optimization
May 26, 2016
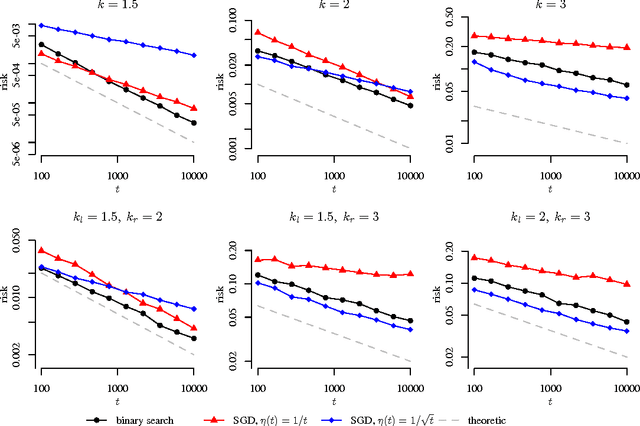
Abstract:We extend the traditional worst-case, minimax analysis of stochastic convex optimization by introducing a localized form of minimax complexity for individual functions. Our main result gives function-specific lower and upper bounds on the number of stochastic subgradient evaluations needed to optimize either the function or its "hardest local alternative" to a given numerical precision. The bounds are expressed in terms of a localized and computational analogue of the modulus of continuity that is central to statistical minimax analysis. We show how the computational modulus of continuity can be explicitly calculated in concrete cases, and relates to the curvature of the function at the optimum. We also prove a superefficiency result that demonstrates it is a meaningful benchmark, acting as a computational analogue of the Fisher information in statistical estimation. The nature and practical implications of the results are demonstrated in simulations.
A Convergent Gradient Descent Algorithm for Rank Minimization and Semidefinite Programming from Random Linear Measurements
Mar 24, 2016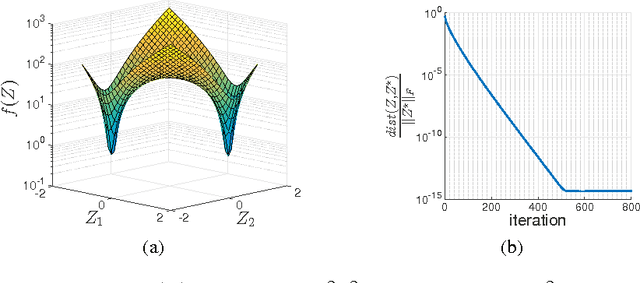

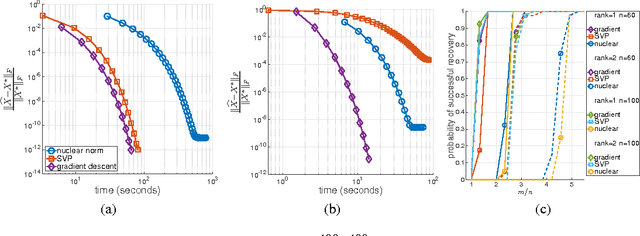
Abstract:We propose a simple, scalable, and fast gradient descent algorithm to optimize a nonconvex objective for the rank minimization problem and a closely related family of semidefinite programs. With $O(r^3 \kappa^2 n \log n)$ random measurements of a positive semidefinite $n \times n$ matrix of rank $r$ and condition number $\kappa$, our method is guaranteed to converge linearly to the global optimum.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge