Quantized Nonparametric Estimation over Sobolev Ellipsoids
Paper and Code
Apr 11, 2017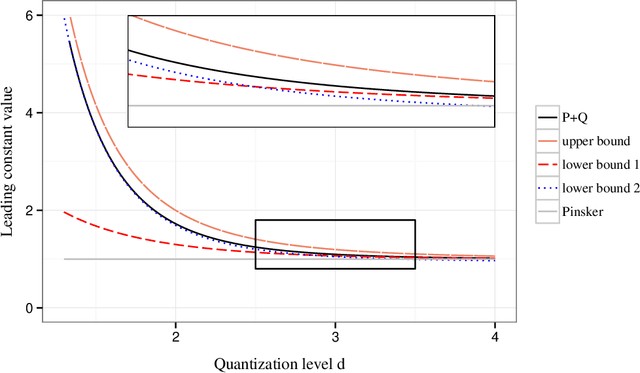
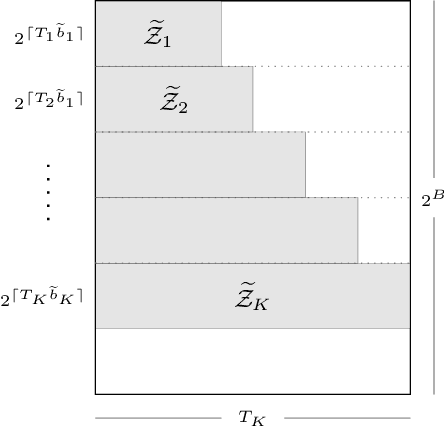
We formulate the notion of minimax estimation under storage or communication constraints, and prove an extension to Pinsker's theorem for nonparametric estimation over Sobolev ellipsoids. Placing limits on the number of bits used to encode any estimator, we give tight lower and upper bounds on the excess risk due to quantization in terms of the number of bits, the signal size, and the noise level. This establishes the Pareto optimal tradeoff between storage and risk under quantization constraints for Sobolev spaces. Our results and proof techniques combine elements of rate distortion theory and minimax analysis. The proposed quantized estimation scheme, which shows achievability of the lower bounds, is adaptive in the usual statistical sense, achieving the optimal quantized minimax rate without knowledge of the smoothness parameter of the Sobolev space. It is also adaptive in a computational sense, as it constructs the code only after observing the data, to dynamically allocate more codewords to blocks where the estimated signal size is large. Simulations are included that illustrate the effect of quantization on statistical risk.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge