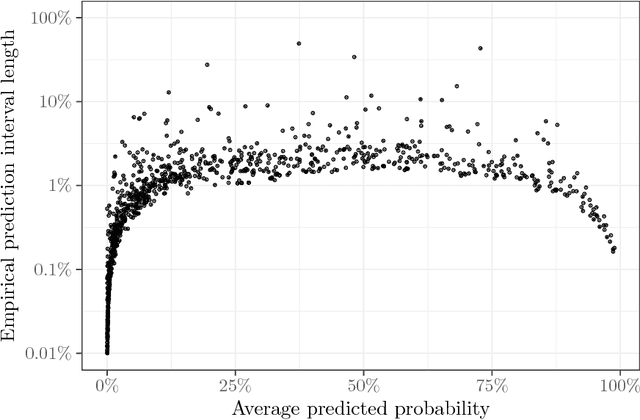
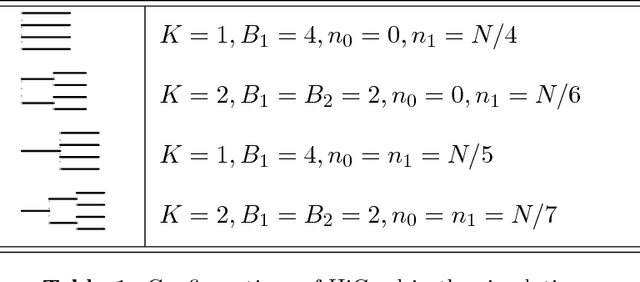
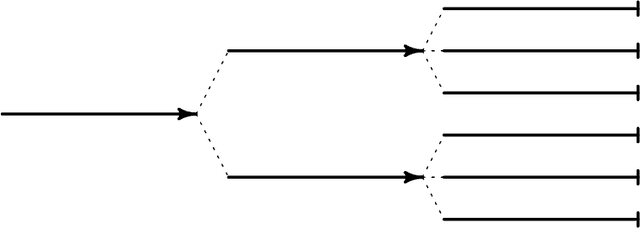
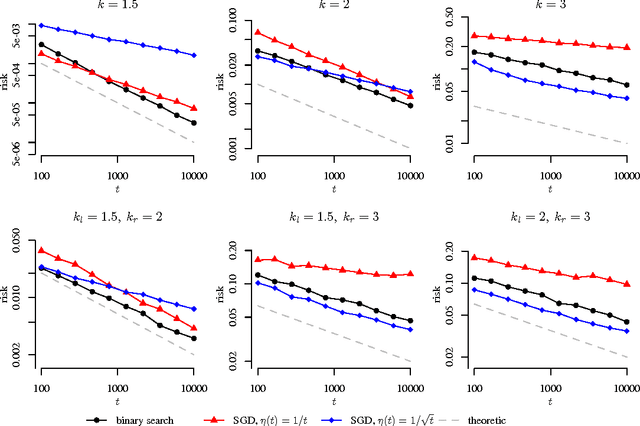
Uncertainty Quantification for Online Learning and Stochastic Approximation via Hierarchical Incremental Gradient Descent

Stochastic gradient descent (SGD) is an immensely popular approach for online learning in settings where data arrives in a stream or data sizes are very large. However, despite an ever- increasing volume of work on SGD, much less is known about the statistical inferential properties of SGD-based predictions. Taking a fully inferential viewpoint, this paper introduces a novel procedure termed HiGrad to conduct statistical inference for online learning, without incurring additional computational cost compared with SGD. The HiGrad procedure begins by performing SGD updates for a while and then splits the single thread into several threads, and this procedure hierarchically operates in this fashion along each thread. With predictions provided by multiple threads in place, a t-based confidence interval is constructed by decorrelating predictions using covariance structures given by a Donsker-style extension of the Ruppert--Polyak averaging scheme, which is a technical contribution of independent interest. Under certain regularity conditions, the HiGrad confidence interval is shown to attain asymptotically exact coverage probability. Finally, the performance of HiGrad is evaluated through extensive simulation studies and a real data example. An R package higrad has been developed to implement the method.

Distributed Nonparametric Regression under Communication Constraints

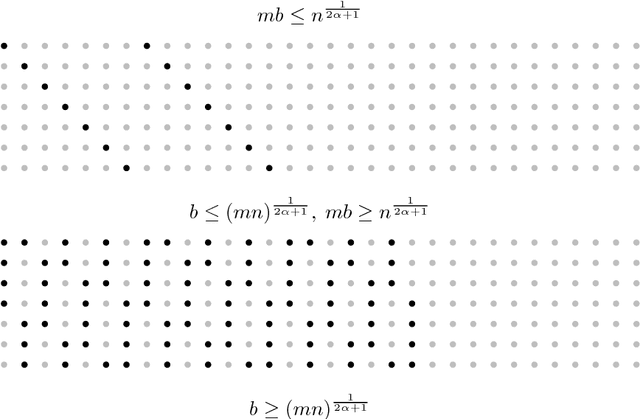
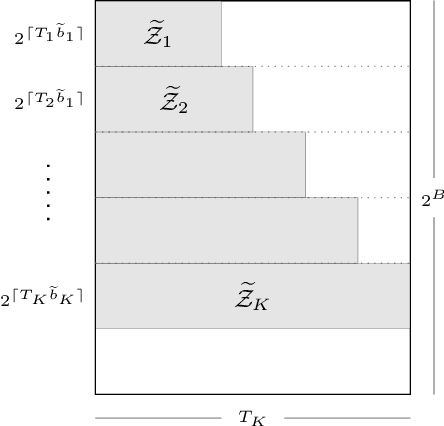
This paper studies the problem of nonparametric estimation of a smooth function with data distributed across multiple machines. We assume an independent sample from a white noise model is collected at each machine, and an estimator of the underlying true function needs to be constructed at a central machine. We place limits on the number of bits that each machine can use to transmit information to the central machine. Our results give both asymptotic lower bounds and matching upper bounds on the statistical risk under various settings. We identify three regimes, depending on the relationship among the number of machines, the size of the data available at each machine, and the communication budget. When the communication budget is small, the statistical risk depends solely on this communication bottleneck, regardless of the sample size. In the regime where the communication budget is large, the classic minimax risk in the non-distributed estimation setting is recovered. In an intermediate regime, the statistical risk depends on both the sample size and the communication budget.

Quantized Nonparametric Estimation over Sobolev Ellipsoids

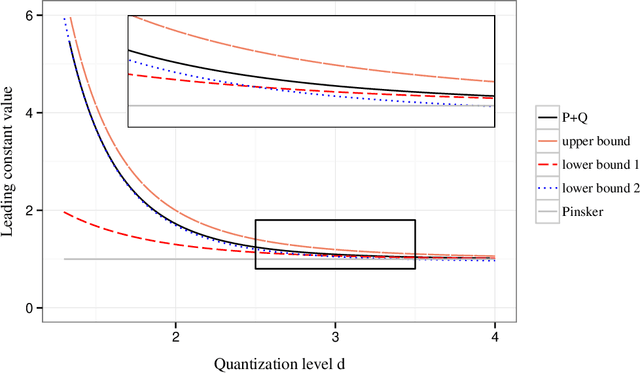
We formulate the notion of minimax estimation under storage or communication constraints, and prove an extension to Pinsker's theorem for nonparametric estimation over Sobolev ellipsoids. Placing limits on the number of bits used to encode any estimator, we give tight lower and upper bounds on the excess risk due to quantization in terms of the number of bits, the signal size, and the noise level. This establishes the Pareto optimal tradeoff between storage and risk under quantization constraints for Sobolev spaces. Our results and proof techniques combine elements of rate distortion theory and minimax analysis. The proposed quantized estimation scheme, which shows achievability of the lower bounds, is adaptive in the usual statistical sense, achieving the optimal quantized minimax rate without knowledge of the smoothness parameter of the Sobolev space. It is also adaptive in a computational sense, as it constructs the code only after observing the data, to dynamically allocate more codewords to blocks where the estimated signal size is large. Simulations are included that illustrate the effect of quantization on statistical risk.

Local Minimax Complexity of Stochastic Convex Optimization

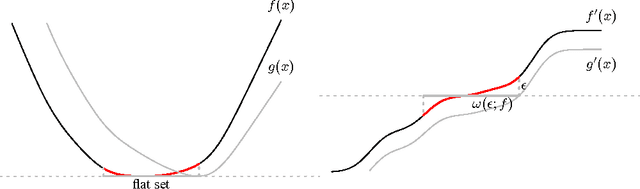
We extend the traditional worst-case, minimax analysis of stochastic convex optimization by introducing a localized form of minimax complexity for individual functions. Our main result gives function-specific lower and upper bounds on the number of stochastic subgradient evaluations needed to optimize either the function or its "hardest local alternative" to a given numerical precision. The bounds are expressed in terms of a localized and computational analogue of the modulus of continuity that is central to statistical minimax analysis. We show how the computational modulus of continuity can be explicitly calculated in concrete cases, and relates to the curvature of the function at the optimum. We also prove a superefficiency result that demonstrates it is a meaningful benchmark, acting as a computational analogue of the Fisher information in statistical estimation. The nature and practical implications of the results are demonstrated in simulations.

Learning Nonparametric Forest Graphical Models with Prior Information

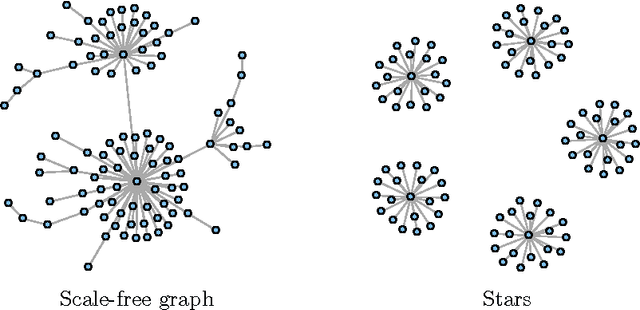
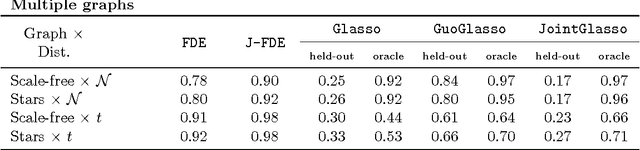
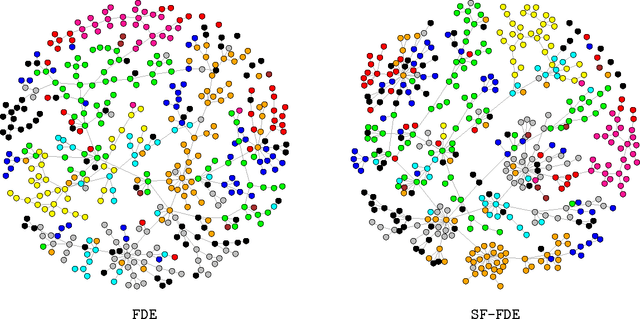
We present a framework for incorporating prior information into nonparametric estimation of graphical models. To avoid distributional assumptions, we restrict the graph to be a forest and build on the work of forest density estimation (FDE). We reformulate the FDE approach from a Bayesian perspective, and introduce prior distributions on the graphs. As two concrete examples, we apply this framework to estimating scale-free graphs and learning multiple graphs with similar structures. The resulting algorithms are equivalent to finding a maximum spanning tree of a weighted graph with a penalty term on the connectivity pattern of the graph. We solve the optimization problem via a minorize-maximization procedure with Kruskal's algorithm. Simulations show that the proposed methods outperform competing parametric methods, and are robust to the true data distribution. They also lead to improvement in predictive power and interpretability in two real data sets.

Quantized Estimation of Gaussian Sequence Models in Euclidean Balls

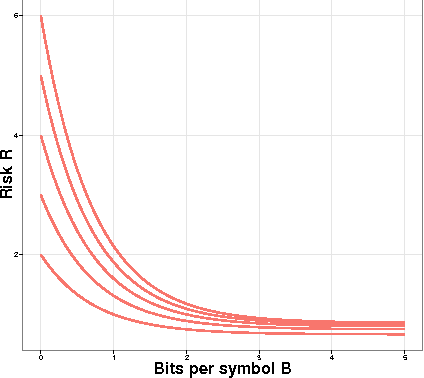
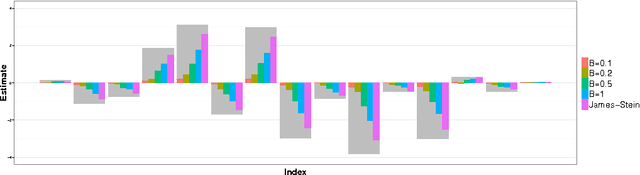
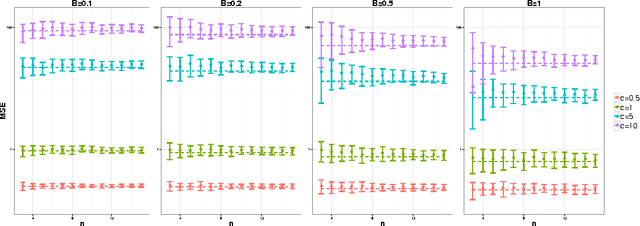
A central result in statistical theory is Pinsker's theorem, which characterizes the minimax rate in the normal means model of nonparametric estimation. In this paper, we present an extension to Pinsker's theorem where estimation is carried out under storage or communication constraints. In particular, we place limits on the number of bits used to encode an estimator, and analyze the excess risk in terms of this constraint, the signal size, and the noise level. We give sharp upper and lower bounds for the case of a Euclidean ball, which establishes the Pareto-optimal minimax tradeoff between storage and risk in this setting.