Convergence Analysis for Rectangular Matrix Completion Using Burer-Monteiro Factorization and Gradient Descent
Paper and Code
Nov 22, 2016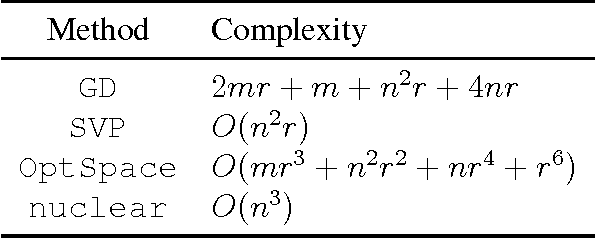
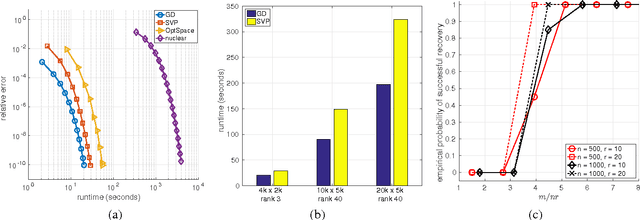
We address the rectangular matrix completion problem by lifting the unknown matrix to a positive semidefinite matrix in higher dimension, and optimizing a nonconvex objective over the semidefinite factor using a simple gradient descent scheme. With $O( \mu r^2 \kappa^2 n \max(\mu, \log n))$ random observations of a $n_1 \times n_2$ $\mu$-incoherent matrix of rank $r$ and condition number $\kappa$, where $n = \max(n_1, n_2)$, the algorithm linearly converges to the global optimum with high probability.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge