Emergent organization of receptive fields in networks of excitatory and inhibitory neurons

Local patterns of excitation and inhibition that can generate neural waves are studied as a computational mechanism underlying the organization of neuronal tunings. Sparse coding algorithms based on networks of excitatory and inhibitory neurons are proposed that exhibit topographic maps as the receptive fields are adapted to input stimuli. Motivated by a leaky integrate-and-fire model of neural waves, we propose an activation model that is more typical of artificial neural networks. Computational experiments with the activation model using both natural images and natural language text are presented. In the case of images, familiar "pinwheel" patterns of oriented edge detectors emerge; in the case of text, the resulting topographic maps exhibit a 2-dimensional representation of granular word semantics. Experiments with a synthetic model of somatosensory input are used to investigate how the network dynamics may affect plasticity of neuronal maps under changes to the inputs.

Convergence and Alignment of Gradient Descent with Random Back Propagation Weights

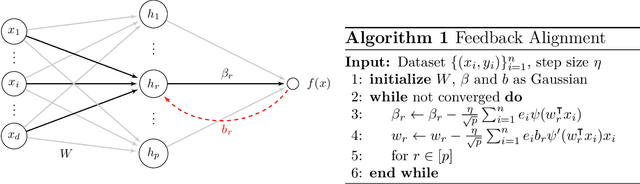
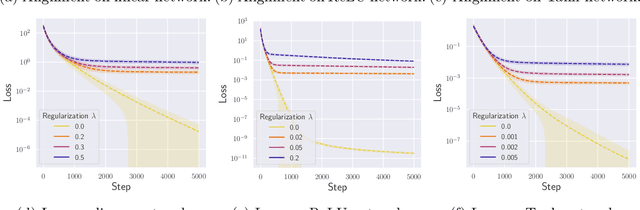
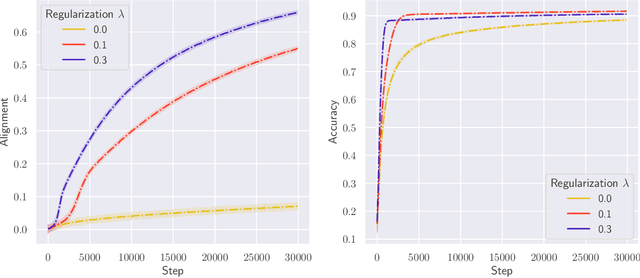
Stochastic gradient descent with backpropagation is the workhorse of artificial neural networks. It has long been recognized that backpropagation fails to be a biologically plausible algorithm. Fundamentally, it is a non-local procedure -- updating one neuron's synaptic weights requires knowledge of synaptic weights or receptive fields of downstream neurons. This limits the use of artificial neural networks as a tool for understanding the biological principles of information processing in the brain. Lillicrap et al. (2016) propose a more biologically plausible "feedback alignment" algorithm that uses random and fixed backpropagation weights, and show promising simulations. In this paper we study the mathematical properties of the feedback alignment procedure by analyzing convergence and alignment for two-layer networks under squared error loss. In the overparameterized setting, we prove that the error converges to zero exponentially fast, and also that regularization is necessary in order for the parameters to become aligned with the random backpropagation weights. Simulations are given that are consistent with this analysis and suggest further generalizations. These results contribute to our understanding of how biologically plausible algorithms might carry out weight learning in a manner different from Hebbian learning, with performance that is comparable with the full non-local backpropagation algorithm.

Surfing: Iterative optimization over incrementally trained deep networks

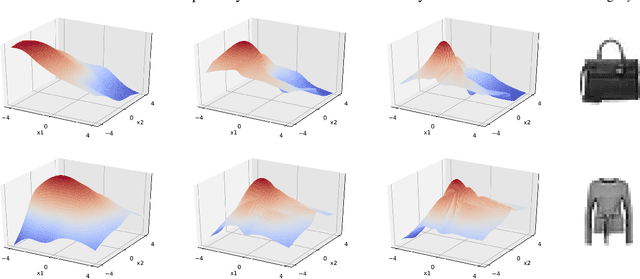
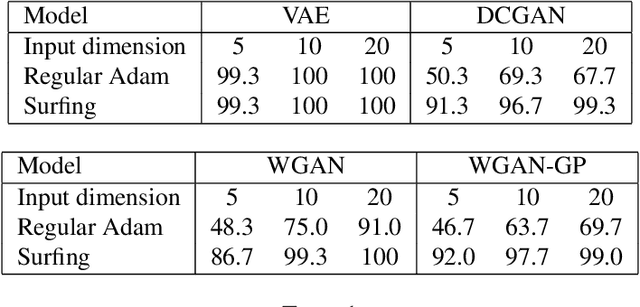
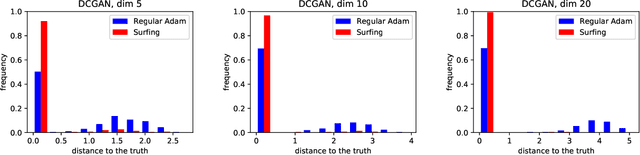
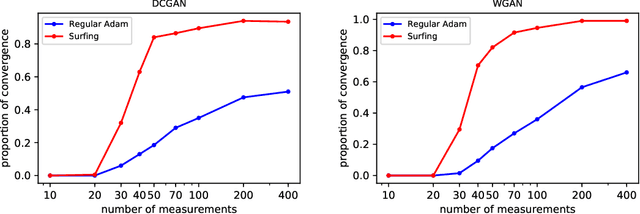
We investigate a sequential optimization procedure to minimize the empirical risk functional $f_{\hat\theta}(x) = \frac{1}{2}\|G_{\hat\theta}(x) - y\|^2$ for certain families of deep networks $G_{\theta}(x)$. The approach is to optimize a sequence of objective functions that use network parameters obtained during different stages of the training process. When initialized with random parameters $\theta_0$, we show that the objective $f_{\theta_0}(x)$ is "nice'' and easy to optimize with gradient descent. As learning is carried out, we obtain a sequence of generative networks $x \mapsto G_{\theta_t}(x)$ and associated risk functions $f_{\theta_t}(x)$, where $t$ indicates a stage of stochastic gradient descent during training. Since the parameters of the network do not change by very much in each step, the surface evolves slowly and can be incrementally optimized. The algorithm is formalized and analyzed for a family of expansive networks. We call the procedure {\it surfing} since it rides along the peak of the evolving (negative) empirical risk function, starting from a smooth surface at the beginning of learning and ending with a wavy nonconvex surface after learning is complete. Experiments show how surfing can be used to find the global optimum and for compressed sensing even when direct gradient descent on the final learned network fails.