Minmax Trend Filtering: A Locally Adaptive Nonparametric Regression Method via Pointwise Min Max Optimization

Trend Filtering is a nonparametric regression method which exhibits local adaptivity, in contrast to a host of classical linear smoothing methods. However, there seems to be no unanimously agreed upon definition of local adaptivity in the literature. A question we seek to answer here is how exactly is Fused Lasso or Total Variation Denoising, which is Trend Filtering of order $0$, locally adaptive? To answer this question, we first derive a new pointwise formula for the Fused Lasso estimator in terms of min-max/max-min optimization of penalized local averages. This pointwise representation appears to be new and gives a concrete explanation of the local adaptivity of Fused Lasso. It yields that the estimation error of Fused Lasso at any given point is bounded by the best (local) bias variance tradeoff where bias and variance have a slightly different meaning than usual. We then propose higher order polynomial versions of Fused Lasso which are defined pointwise in terms of min-max/max-min optimization of penalized local polynomial regressions. These appear to be new nonparametric regression methods, different from any existing method in the nonparametric regression toolbox. We call these estimators Minmax Trend Filtering. They continue to enjoy the notion of local adaptivity in the sense that their estimation error at any given point is bounded by the best (local) bias variance tradeoff.

Spatially Adaptive Online Prediction of Piecewise Regular Functions

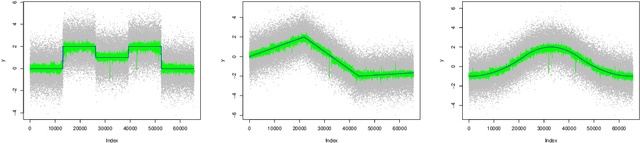
We consider the problem of estimating piecewise regular functions in an online setting, i.e., the data arrive sequentially and at any round our task is to predict the value of the true function at the next revealed point using the available data from past predictions. We propose a suitably modified version of a recently developed online learning algorithm called the sleeping experts aggregation algorithm. We show that this estimator satisfies oracle risk bounds simultaneously for all local regions of the domain. As concrete instantiations of the expert aggregation algorithm proposed here, we study an online mean aggregation and an online linear regression aggregation algorithm where experts correspond to the set of dyadic subrectangles of the domain. The resulting algorithms are near linear time computable in the sample size. We specifically focus on the performance of these online algorithms in the context of estimating piecewise polynomial and bounded variation function classes in the fixed design setup. The simultaneous oracle risk bounds we obtain for these estimators in this context provide new and improved (in certain aspects) guarantees even in the batch setting and are not available for the state of the art batch learning estimators.

A Cross Validation Framework for Signal Denoising with Applications to Trend Filtering, Dyadic CART and Beyond

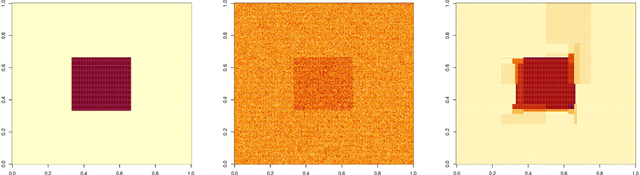
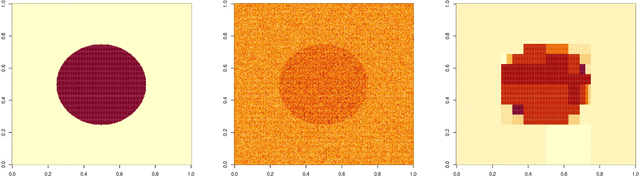
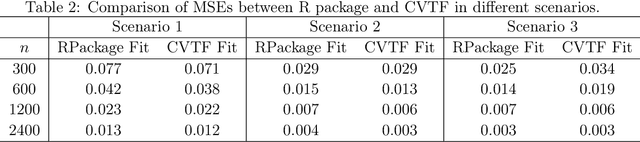
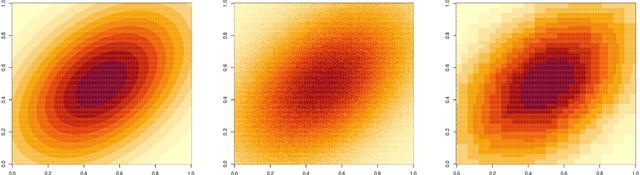
This paper formulates a general cross validation framework for signal denoising. The general framework is then applied to nonparametric regression methods such as Trend Filtering and Dyadic CART. The resulting cross validated versions are then shown to attain nearly the same rates of convergence as are known for the optimally tuned analogues. There did not exist any previous theoretical analyses of cross validated versions of Trend Filtering or Dyadic CART. To illustrate the generality of the framework we also propose and study cross validated versions of two fundamental estimators; lasso for high dimensional linear regression and singular value thresholding for matrix estimation. Our general framework is inspired by the ideas in Chatterjee and Jafarov (2015) and is potentially applicable to a wide range of estimation methods which use tuning parameters.

Adaptive Estimation of Multivariate Piecewise Polynomials and Bounded Variation Functions by Optimal Decision Trees

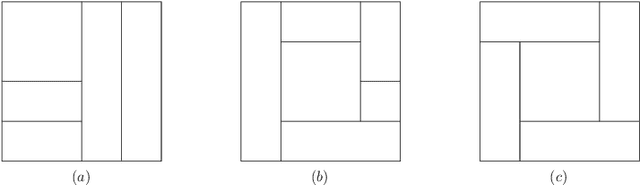
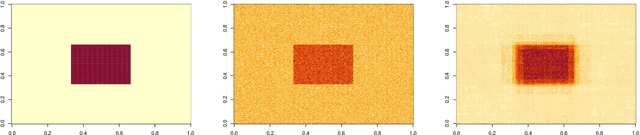
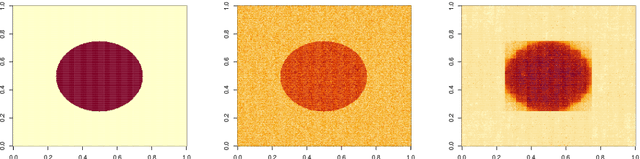
Proposed by \cite{donoho1997cart}, Dyadic CART is a nonparametric regression method which computes a globally optimal dyadic decision tree and fits piecewise constant functions in two dimensions. In this article we define and study Dyadic CART and a closely related estimator, namely Optimal Regression Tree (ORT), in the context of estimating piecewise smooth functions in general dimensions. More precisely, these optimal decision tree estimators fit piecewise polynomials of any given degree. Like Dyadic CART in two dimensions, we reason that these estimators can also be computed in polynomial time in the sample size via dynamic programming. We prove oracle inequalities for the finite sample risk of Dyadic CART and ORT which imply tight {risk} bounds for several function classes of interest. Firstly, they imply that the finite sample risk of ORT of {\em order} $r \geq 0$ is always bounded by $C k \frac{\log N}{N}$ ($N$ is the sample size) whenever the regression function is piecewise polynomial of degree $r$ on some reasonably regular axis aligned rectangular partition of the domain with at most $k$ rectangles. Beyond the univariate case, such guarantees are scarcely available in the literature for computationally efficient estimators. Secondly, our oracle inequalities uncover minimax rate optimality and adaptivity of the Dyadic CART estimator for function spaces with bounded variation. We consider two function spaces of recent interest where multivariate total variation denoising and univariate trend filtering are the state of the art methods. We show that Dyadic CART enjoys certain advantages over these estimators while still maintaining all their known guarantees.

New Risk Bounds for 2D Total Variation Denoising

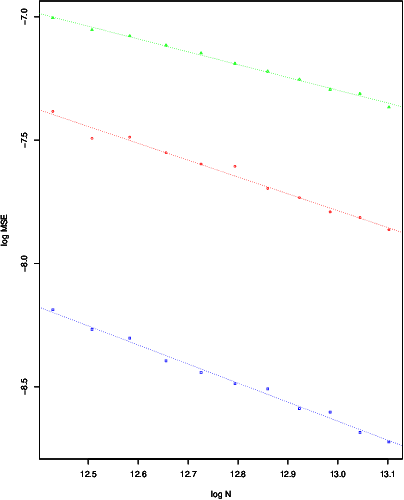
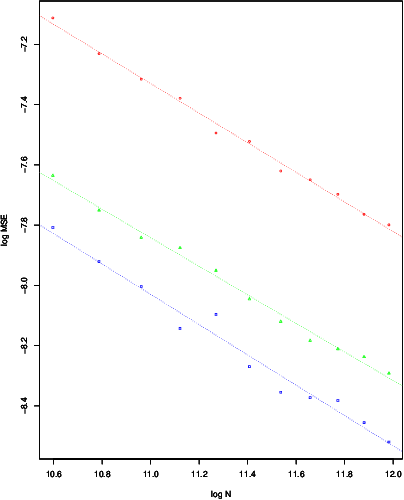
2D Total Variation Denoising (TVD) is a widely used technique for image denoising. It is also an important non parametric regression method for estimating functions with heterogenous smoothness. Recent results have shown the TVD estimator to be nearly minimax rate optimal for the class of functions with bounded variation. In this paper, we complement these worst case guarantees by investigating the adaptivity of the TVD estimator to functions which are piecewise constant on axis aligned rectangles. We rigorously show that, when the truth is piecewise constant, the ideally tuned TVD estimator performs better than in the worst case. We also study the issue of choosing the tuning parameter. In particular, we propose a fully data driven version of the TVD estimator which enjoys similar worst case risk guarantees as the ideally tuned TVD estimator.

Prediction Rule Reshaping

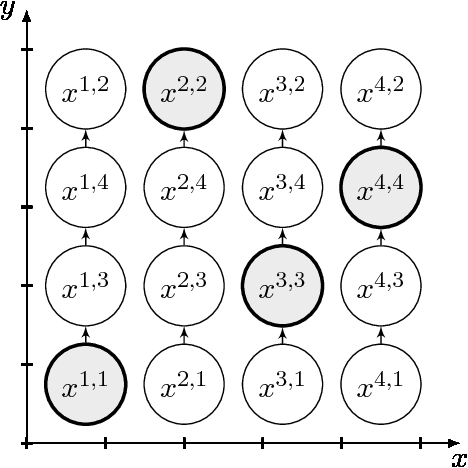
Two methods are proposed for high-dimensional shape-constrained regression and classification. These methods reshape pre-trained prediction rules to satisfy shape constraints like monotonicity and convexity. The first method can be applied to any pre-trained prediction rule, while the second method deals specifically with random forests. In both cases, efficient algorithms are developed for computing the estimators, and experiments are performed to demonstrate their performance on four datasets. We find that reshaping methods enforce shape constraints without compromising predictive accuracy.

Local Minimax Complexity of Stochastic Convex Optimization

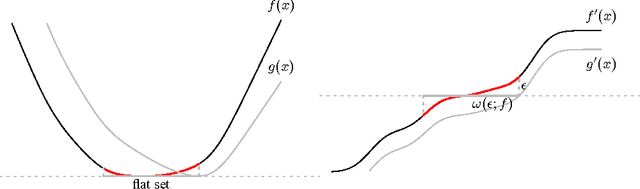
We extend the traditional worst-case, minimax analysis of stochastic convex optimization by introducing a localized form of minimax complexity for individual functions. Our main result gives function-specific lower and upper bounds on the number of stochastic subgradient evaluations needed to optimize either the function or its "hardest local alternative" to a given numerical precision. The bounds are expressed in terms of a localized and computational analogue of the modulus of continuity that is central to statistical minimax analysis. We show how the computational modulus of continuity can be explicitly calculated in concrete cases, and relates to the curvature of the function at the optimum. We also prove a superefficiency result that demonstrates it is a meaningful benchmark, acting as a computational analogue of the Fisher information in statistical estimation. The nature and practical implications of the results are demonstrated in simulations.