A Convergent Gradient Descent Algorithm for Rank Minimization and Semidefinite Programming from Random Linear Measurements
Paper and Code
Mar 24, 2016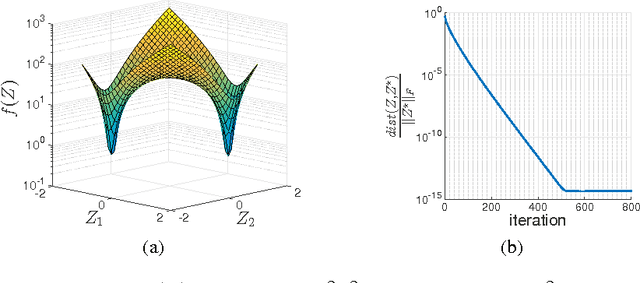

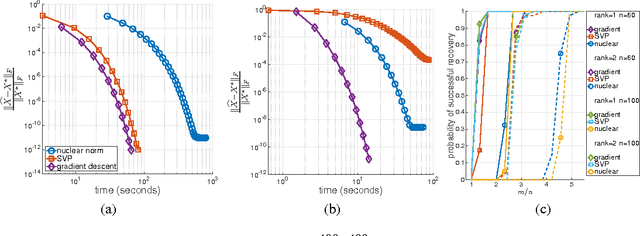
We propose a simple, scalable, and fast gradient descent algorithm to optimize a nonconvex objective for the rank minimization problem and a closely related family of semidefinite programs. With $O(r^3 \kappa^2 n \log n)$ random measurements of a positive semidefinite $n \times n$ matrix of rank $r$ and condition number $\kappa$, our method is guaranteed to converge linearly to the global optimum.
* Fix a minor error in Appendix E
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge