STAR-Net: An Interpretable Model-Aided Network for Remote Sensing Image Denoising

Remote sensing image (RSI) denoising is an important topic in the field of remote sensing. Despite the impressive denoising performance of RSI denoising methods, most current deep learning-based approaches function as black boxes and lack integration with physical information models, leading to limited interpretability. Additionally, many methods may struggle with insufficient attention to non-local self-similarity in RSI and require tedious tuning of regularization parameters to achieve optimal performance, particularly in conventional iterative optimization approaches. In this paper, we first propose a novel RSI denoising method named sparse tensor-aided representation network (STAR-Net), which leverages a low-rank prior to effectively capture the non-local self-similarity within RSI. Furthermore, we extend STAR-Net to a sparse variant called STAR-Net-S to deal with the interference caused by non-Gaussian noise in original RSI for the purpose of improving robustness. Different from conventional iterative optimization, we develop an alternating direction method of multipliers (ADMM)-guided deep unrolling network, in which all regularization parameters can be automatically learned, thus inheriting the advantages of both model-based and deep learning-based approaches and successfully addressing the above-mentioned shortcomings. Comprehensive experiments on synthetic and real-world datasets demonstrate that STAR-Net and STAR-Net-S outperform state-of-the-art RSI denoising methods.

Counting Cycles with Deepseek

Despite recent progress, AI still struggles on advanced mathematics. We consider a difficult open problem: How to derive a Computationally Efficient Equivalent Form (CEEF) for the cycle count statistic? The CEEF problem does not have known general solutions, and requires delicate combinatorics and tedious calculations. Such a task is hard to accomplish by humans but is an ideal example where AI can be very helpful. We solve the problem by combining a novel approach we propose and the powerful coding skills of AI. Our results use delicate graph theory and contain new formulas for general cases that have not been discovered before. We find that, while AI is unable to solve the problem all by itself, it is able to solve it if we provide it with a clear strategy, a step-by-step guidance and carefully written prompts. For simplicity, we focus our study on DeepSeek-R1 but we also investigate other AI approaches.

Fitting networks with a cancellation trick

The degree-corrected block model (DCBM), latent space model (LSM), and $\beta$-model are all popular network models. We combine their modeling ideas and propose the logit-DCBM as a new model. Similar as the $\beta$-model and LSM, the logit-DCBM contains nonlinear factors, where fitting the parameters is a challenging open problem. We resolve this problem by introducing a cancellation trick. We also propose R-SCORE as a recursive community detection algorithm, where in each iteration, we first use the idea above to update our parameter estimation, and then use the results to remove the nonlinear factors in the logit-DCBM so the renormalized model approximately satisfies a low-rank model, just like the DCBM. Our numerical study suggests that R-SCORE significantly improves over existing spectral approaches in many cases. Also, theoretically, we show that the Hamming error rate of R-SCORE is faster than that of SCORE in a specific sparse region, and is at least as fast outside this region.

A Comparison of DeepSeek and Other LLMs

Recently, DeepSeek has been the focus of attention in and beyond the AI community. An interesting problem is how DeepSeek compares to other large language models (LLMs). There are many tasks an LLM can do, and in this paper, we use the task of predicting an outcome using a short text for comparison. We consider two settings, an authorship classification setting and a citation classification setting. In the first one, the goal is to determine whether a short text is written by human or AI. In the second one, the goal is to classify a citation to one of four types using the textual content. For each experiment, we compare DeepSeek with $4$ popular LLMs: Claude, Gemini, GPT, and Llama. We find that, in terms of classification accuracy, DeepSeek outperforms Gemini, GPT, and Llama in most cases, but underperforms Claude. We also find that DeepSeek is comparably slower than others but with a low cost to use, while Claude is much more expensive than all the others. Finally, we find that in terms of similarity, the output of DeepSeek is most similar to those of Gemini and Claude (and among all $5$ LLMs, Claude and Gemini have the most similar outputs). In this paper, we also present a fully-labeled dataset collected by ourselves, and propose a recipe where we can use the LLMs and a recent data set, MADStat, to generate new data sets. The datasets in our paper can be used as benchmarks for future study on LLMs.

Improved Algorithm and Bounds for Successive Projection

Given a $K$-vertex simplex in a $d$-dimensional space, suppose we measure $n$ points on the simplex with noise (hence, some of the observed points fall outside the simplex). Vertex hunting is the problem of estimating the $K$ vertices of the simplex. A popular vertex hunting algorithm is successive projection algorithm (SPA). However, SPA is observed to perform unsatisfactorily under strong noise or outliers. We propose pseudo-point SPA (pp-SPA). It uses a projection step and a denoise step to generate pseudo-points and feed them into SPA for vertex hunting. We derive error bounds for pp-SPA, leveraging on extreme value theory of (possibly) high-dimensional random vectors. The results suggest that pp-SPA has faster rates and better numerical performances than SPA. Our analysis includes an improved non-asymptotic bound for the original SPA, which is of independent interest.

Recent Advances in Text Analysis

Text analysis is an interesting research area in data science and has various applications, such as in artificial intelligence, biomedical research, and engineering. We review popular methods for text analysis, ranging from topic modeling to the recent neural language models. In particular, we review Topic-SCORE, a statistical approach to topic modeling, and discuss how to use it to analyze MADStat - a dataset on statistical publications that we collected and cleaned. The application of Topic-SCORE and other methods on MADStat leads to interesting findings. For example, $11$ representative topics in statistics are identified. For each journal, the evolution of topic weights over time can be visualized, and these results are used to analyze the trends in statistical research. In particular, we propose a new statistical model for ranking the citation impacts of $11$ topics, and we also build a cross-topic citation graph to illustrate how research results on different topics spread to one another. The results on MADStat provide a data-driven picture of the statistical research in $1975$--$2015$, from a text analysis perspective.

Subject clustering by IF-PCA and several recent methods

Subject clustering (i.e., the use of measured features to cluster subjects, such as patients or cells, into multiple groups) is a problem of great interest. In recent years, many approaches were proposed, among which unsupervised deep learning (UDL) has received a great deal of attention. Two interesting questions are (a) how to combine the strengths of UDL and other approaches, and (b) how these approaches compare to one other. We combine Variational Auto-Encoder (VAE), a popular UDL approach, with the recent idea of Influential Feature PCA (IF-PCA), and propose IF-VAE as a new method for subject clustering. We study IF-VAE and compare it with several other methods (including IF-PCA, VAE, Seurat, and SC3) on $10$ gene microarray data sets and $8$ single-cell RNA-seq data sets. We find that IF-VAE significantly improves over VAE, but still underperforms IF-PCA. We also find that IF-PCA is quite competitive, which slightly outperforms Seurat and SC3 over the $8$ single-cell data sets. IF-PCA is conceptually simple and permits delicate analysis. We demonstrate that IF-PCA is capable of achieving the phase transition in a Rare/Weak model. Comparatively, Seurat and SC3 are more complex and theoretically difficult to analyze (for these reasons, their optimality remains unclear).

Phase transition for detecting a small community in a large network

How to detect a small community in a large network is an interesting problem, including clique detection as a special case, where a naive degree-based $\chi^2$-test was shown to be powerful in the presence of an Erd\H{o}s-Renyi background. Using Sinkhorn's theorem, we show that the signal captured by the $\chi^2$-test may be a modeling artifact, and it may disappear once we replace the Erd\H{o}s-Renyi model by a broader network model. We show that the recent SgnQ test is more appropriate for such a setting. The test is optimal in detecting communities with sizes comparable to the whole network, but has never been studied for our setting, which is substantially different and more challenging. Using a degree-corrected block model (DCBM), we establish phase transitions of this testing problem concerning the size of the small community and the edge densities in small and large communities. When the size of the small community is larger than $\sqrt{n}$, the SgnQ test is optimal for it attains the computational lower bound (CLB), the information lower bound for methods allowing polynomial computation time. When the size of the small community is smaller than $\sqrt{n}$, we establish the parameter regime where the SgnQ test has full power and make some conjectures of the CLB. We also study the classical information lower bound (LB) and show that there is always a gap between the CLB and LB in our range of interest.

SCORE+ for Network Community Detection

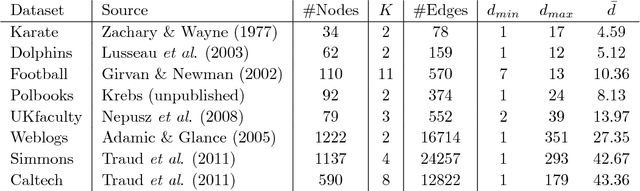
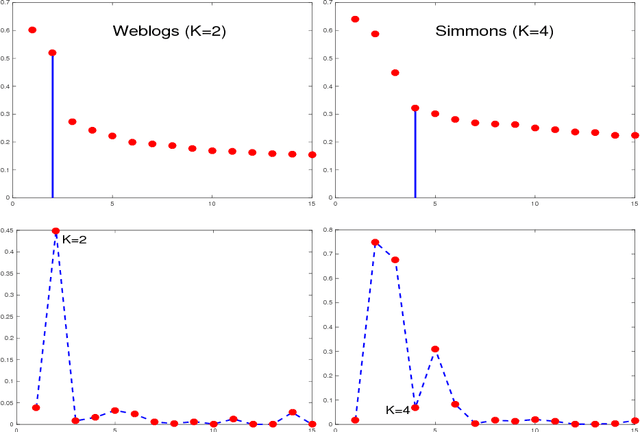
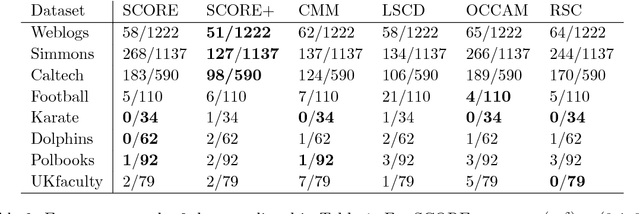
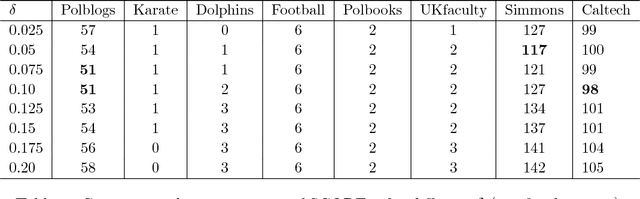
SCORE is a recent approach to network community detection proposed by Jin (2015). In this note, we propose a simple improvement of SCORE, called SCORE+, and compare its performance with several other methods, using 10 different network data sets. For 7 of these data sets, the performances of SCORE and SCORE+ are similar, but for the other 3 data sets (Polbooks, Simmons, Caltech), SCORE+ provides a significant improvement.

Phase Transitions for High Dimensional Clustering and Related Problems

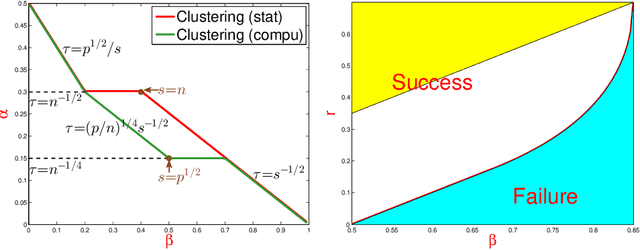
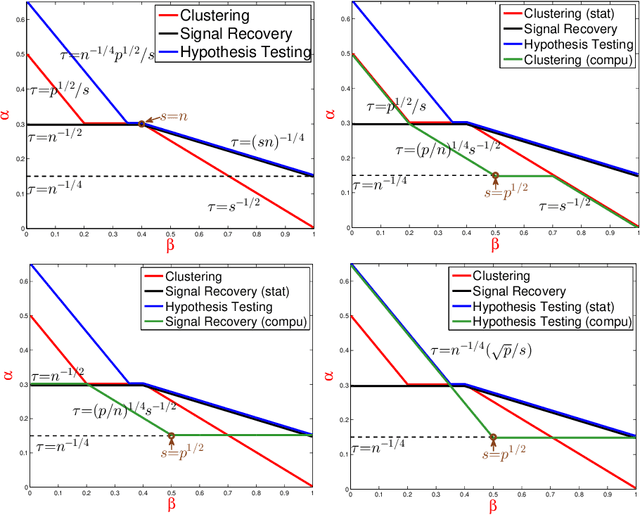
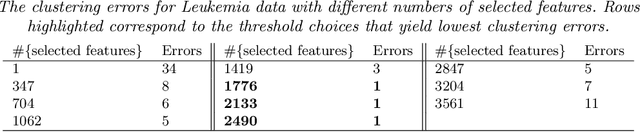
Consider a two-class clustering problem where we observe $X_i = \ell_i \mu + Z_i$, $Z_i \stackrel{iid}{\sim} N(0, I_p)$, $1 \leq i \leq n$. The feature vector $\mu\in R^p$ is unknown but is presumably sparse. The class labels $\ell_i\in\{-1, 1\}$ are also unknown and the main interest is to estimate them. We are interested in the statistical limits. In the two-dimensional phase space calibrating the rarity and strengths of useful features, we find the precise demarcation for the Region of Impossibility and Region of Possibility. In the former, useful features are too rare/weak for successful clustering. In the latter, useful features are strong enough to allow successful clustering. The results are extended to the case of colored noise using Le Cam's idea on comparison of experiments. We also extend the study on statistical limits for clustering to that for signal recovery and that for hypothesis testing. We compare the statistical limits for three problems and expose some interesting insight. We propose classical PCA and Important Features PCA (IF-PCA) for clustering. For a threshold $t > 0$, IF-PCA clusters by applying classical PCA to all columns of $X$ with an $L^2$-norm larger than $t$. We also propose two aggregation methods. For any parameter in the Region of Possibility, some of these methods yield successful clustering. We find an interesting phase transition for IF-PCA. Our results require delicate analysis, especially on post-selection Random Matrix Theory and on lower bound arguments.