i-IF-Learn: Iterative Feature Selection and Unsupervised Learning for High-Dimensional Complex Data

Unsupervised learning of high-dimensional data is challenging due to irrelevant or noisy features obscuring underlying structures. It's common that only a few features, called the influential features, meaningfully define the clusters. Recovering these influential features is helpful in data interpretation and clustering. We propose i-IF-Learn, an iterative unsupervised framework that jointly performs feature selection and clustering. Our core innovation is an adaptive feature selection statistic that effectively combines pseudo-label supervision with unsupervised signals, dynamically adjusting based on intermediate label reliability to mitigate error propagation common in iterative frameworks. Leveraging low-dimensional embeddings (PCA or Laplacian eigenmaps) followed by $k$-means, i-IF-Learn simultaneously outputs influential feature subset and clustering labels. Numerical experiments on gene microarray and single-cell RNA-seq datasets show that i-IF-Learn significantly surpasses classical and deep clustering baselines. Furthermore, using our selected influential features as preprocessing substantially enhances downstream deep models such as DeepCluster, UMAP, and VAE, highlighting the importance and effectiveness of targeted feature selection.

Phase Transitions for High Dimensional Clustering and Related Problems

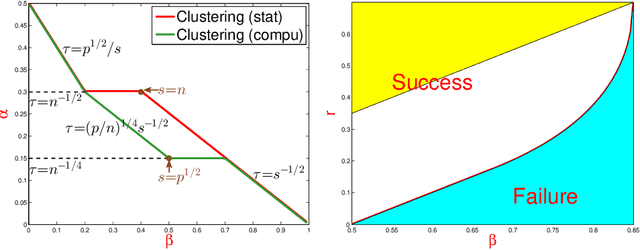
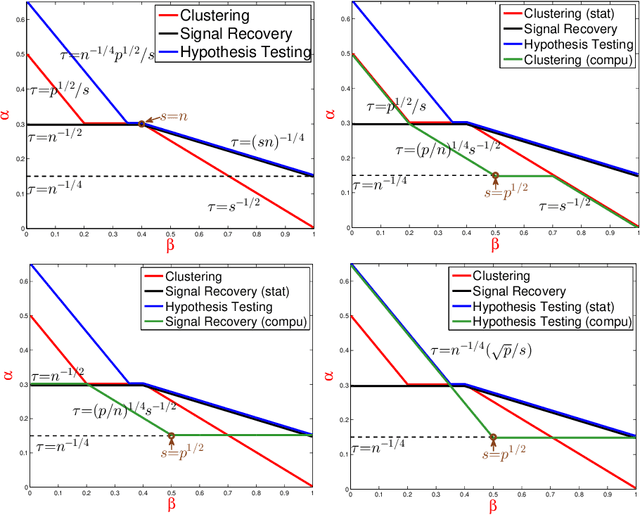
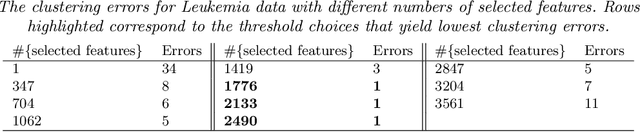
Consider a two-class clustering problem where we observe $X_i = \ell_i \mu + Z_i$, $Z_i \stackrel{iid}{\sim} N(0, I_p)$, $1 \leq i \leq n$. The feature vector $\mu\in R^p$ is unknown but is presumably sparse. The class labels $\ell_i\in\{-1, 1\}$ are also unknown and the main interest is to estimate them. We are interested in the statistical limits. In the two-dimensional phase space calibrating the rarity and strengths of useful features, we find the precise demarcation for the Region of Impossibility and Region of Possibility. In the former, useful features are too rare/weak for successful clustering. In the latter, useful features are strong enough to allow successful clustering. The results are extended to the case of colored noise using Le Cam's idea on comparison of experiments. We also extend the study on statistical limits for clustering to that for signal recovery and that for hypothesis testing. We compare the statistical limits for three problems and expose some interesting insight. We propose classical PCA and Important Features PCA (IF-PCA) for clustering. For a threshold $t > 0$, IF-PCA clusters by applying classical PCA to all columns of $X$ with an $L^2$-norm larger than $t$. We also propose two aggregation methods. For any parameter in the Region of Possibility, some of these methods yield successful clustering. We find an interesting phase transition for IF-PCA. Our results require delicate analysis, especially on post-selection Random Matrix Theory and on lower bound arguments.