Lightweight Deep Unfolding Networks with Enhanced Robustness for Infrared Small Target Detection

Infrared small target detection (ISTD) is one of the key techniques in image processing. Although deep unfolding networks (DUNs) have demonstrated promising performance in ISTD due to their model interpretability and data adaptability, existing methods still face significant challenges in parameter lightweightness and noise robustness. In this regard, we propose a highly lightweight framework based on robust principal component analysis (RPCA) called L-RPCANet. Technically, a hierarchical bottleneck structure is constructed to reduce and increase the channel dimension in the single-channel input infrared image to achieve channel-wise feature refinement, with bottleneck layers designed in each module to extract features. This reduces the number of channels in feature extraction and improves the lightweightness of network parameters. Furthermore, a noise reduction module is embedded to enhance the robustness against complex noise. In addition, squeeze-and-excitation networks (SENets) are leveraged as a channel attention mechanism to focus on the varying importance of different features across channels, thereby achieving excellent performance while maintaining both lightweightness and robustness. Extensive experiments on the ISTD datasets validate the superiority of our proposed method compared with state-of-the-art methods covering RPCANet, DRPCANet, and RPCANet++. The code will be available at https://github.com/xianchaoxiu/L-RPCANet.

Transformer-Guided Content-Adaptive Graph Learning for Hyperspectral Unmixing

Hyperspectral unmixing (HU) targets to decompose each mixed pixel in remote sensing images into a set of endmembers and their corresponding abundances. Despite significant progress in this field using deep learning, most methods fail to simultaneously characterize global dependencies and local consistency, making it difficult to preserve both long-range interactions and boundary details. This letter proposes a novel transformer-guided content-adaptive graph unmixing framework (T-CAGU), which overcomes these challenges by employing a transformer to capture global dependencies and introducing a content-adaptive graph neural network to enhance local relationships. Unlike previous work, T-CAGU integrates multiple propagation orders to dynamically learn the graph structure, ensuring robustness against noise. Furthermore, T-CAGU leverages a graph residual mechanism to preserve global information and stabilize training. Experimental results demonstrate its superiority over the state-of-the-art methods. Our code is available at https://github.com/xianchaoxiu/T-CAGU.

STAR-Net: An Interpretable Model-Aided Network for Remote Sensing Image Denoising

Remote sensing image (RSI) denoising is an important topic in the field of remote sensing. Despite the impressive denoising performance of RSI denoising methods, most current deep learning-based approaches function as black boxes and lack integration with physical information models, leading to limited interpretability. Additionally, many methods may struggle with insufficient attention to non-local self-similarity in RSI and require tedious tuning of regularization parameters to achieve optimal performance, particularly in conventional iterative optimization approaches. In this paper, we first propose a novel RSI denoising method named sparse tensor-aided representation network (STAR-Net), which leverages a low-rank prior to effectively capture the non-local self-similarity within RSI. Furthermore, we extend STAR-Net to a sparse variant called STAR-Net-S to deal with the interference caused by non-Gaussian noise in original RSI for the purpose of improving robustness. Different from conventional iterative optimization, we develop an alternating direction method of multipliers (ADMM)-guided deep unrolling network, in which all regularization parameters can be automatically learned, thus inheriting the advantages of both model-based and deep learning-based approaches and successfully addressing the above-mentioned shortcomings. Comprehensive experiments on synthetic and real-world datasets demonstrate that STAR-Net and STAR-Net-S outperform state-of-the-art RSI denoising methods.

Bi-Level Unsupervised Feature Selection

Unsupervised feature selection (UFS) is an important task in data engineering. However, most UFS methods construct models from a single perspective and often fail to simultaneously evaluate feature importance and preserve their inherent data structure, thus limiting their performance. To address this challenge, we propose a novel bi-level unsupervised feature selection (BLUFS) method, including a clustering level and a feature level. Specifically, at the clustering level, spectral clustering is used to generate pseudo-labels for representing the data structure, while a continuous linear regression model is developed to learn the projection matrix. At the feature level, the $\ell_{2,0}$-norm constraint is imposed on the projection matrix for more effectively selecting features. To the best of our knowledge, this is the first work to combine a bi-level framework with the $\ell_{2,0}$-norm. To solve the proposed bi-level model, we design an efficient proximal alternating minimization (PAM) algorithm, whose subproblems either have explicit solutions or can be computed by fast solvers. Furthermore, we establish the convergence result and computational complexity. Finally, extensive experiments on two synthetic datasets and eight real datasets demonstrate the superiority of BLUFS in clustering and classification tasks.

Robust Orthogonal NMF with Label Propagation for Image Clustering

Non-negative matrix factorization (NMF) is a popular unsupervised learning approach widely used in image clustering. However, in real-world clustering scenarios, most existing NMF methods are highly sensitive to noise corruption and are unable to effectively leverage limited supervised information. To overcome these drawbacks, we propose a unified non-convex framework with label propagation called robust orthogonal nonnegative matrix factorization (RONMF). This method not only considers the graph Laplacian and label propagation as regularization terms but also introduces a more effective non-convex structure to measure the reconstruction error and imposes orthogonal constraints on the basis matrix to reduce the noise corruption, thereby achieving higher robustness. To solve RONMF, we develop an alternating direction method of multipliers (ADMM)-based optimization algorithm. In particular, all subproblems have closed-form solutions, which ensures its efficiency. Experimental evaluations on eight public image datasets demonstrate that the proposed RONMF outperforms state-of-the-art NMF methods across various standard metrics and shows excellent robustness. The code will be available at https://github.com/slinda-liu.

Federated Structured Sparse PCA for Anomaly Detection in IoT Networks

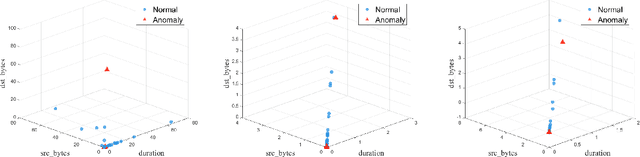
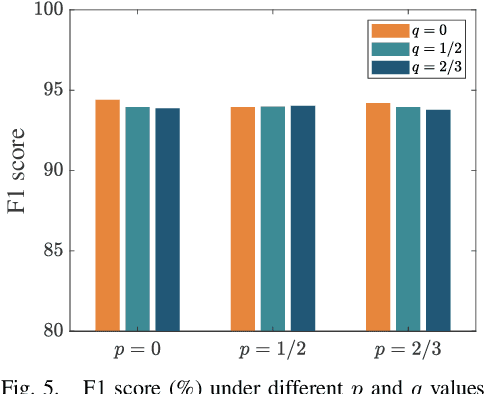
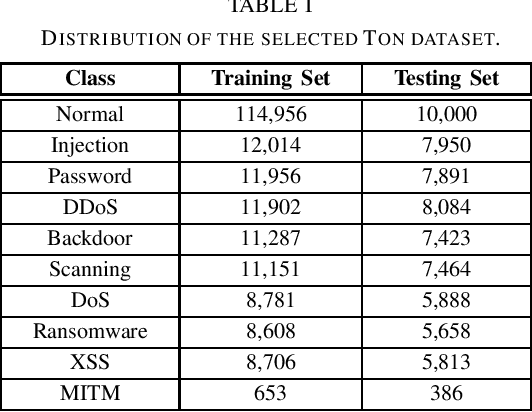
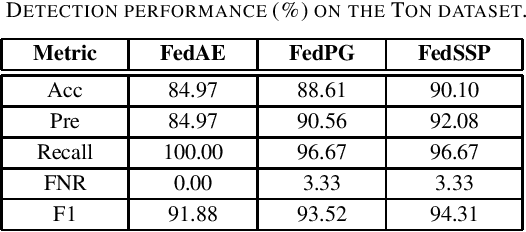
Although federated learning has gained prominence as a privacy-preserving framework tailored for distributed Internet of Things (IoT) environments, current federated principal component analysis (PCA) methods lack integration of sparsity, a critical feature for robust anomaly detection. To address this limitation, we propose a novel federated structured sparse PCA (FedSSP) approach for anomaly detection in IoT networks. The proposed model uniquely integrates double sparsity regularization: (1) row-wise sparsity governed by $\ell_{2,p}$-norm with $p\in[0,1)$ to eliminate redundant feature dimensions, and (2) element-wise sparsity via $\ell_{q}$-norm with $q\in[0,1)$ to suppress noise-sensitive components. To efficiently solve this non-convex optimization problem in a distributed setting, we devise a proximal alternating minimization (PAM) algorithm with rigorous theoretical proofs establishing its convergence guarantees. Experiments on real datasets validate that incorporating structured sparsity enhances both model interpretability and detection accuracy.

LLM4FS: Leveraging Large Language Models for Feature Selection and How to Improve It

Recent advances in large language models (LLMs) have provided new opportunities for decision-making, particularly in the task of automated feature selection. In this paper, we first comprehensively evaluate LLM-based feature selection methods, covering the state-of-the-art DeepSeek-R1, GPT-o3-mini, and GPT-4.5. Then, we propose a novel hybrid strategy called LLM4FS that integrates LLMs with traditional data-driven methods. Specifically, input data samples into LLMs, and directly call traditional data-driven techniques such as random forest and forward sequential selection. Notably, our analysis reveals that the hybrid strategy leverages the contextual understanding of LLMs and the high statistical reliability of traditional data-driven methods to achieve excellent feature selection performance, even surpassing LLMs and traditional data-driven methods. Finally, we point out the limitations of its application in decision-making.

Adaptive Multi-Order Graph Regularized NMF with Dual Sparsity for Hyperspectral Unmixing

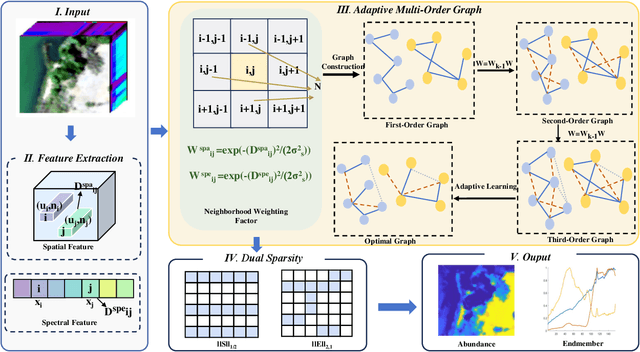
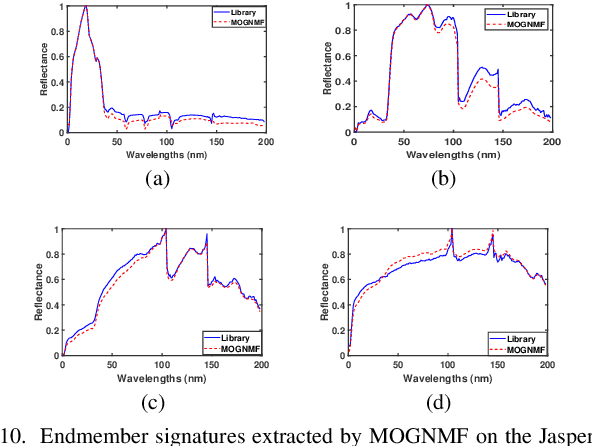
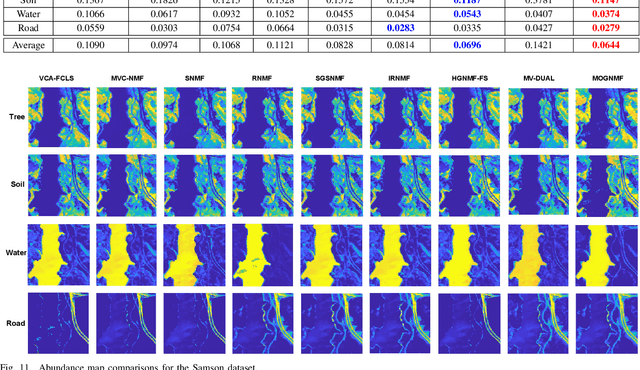
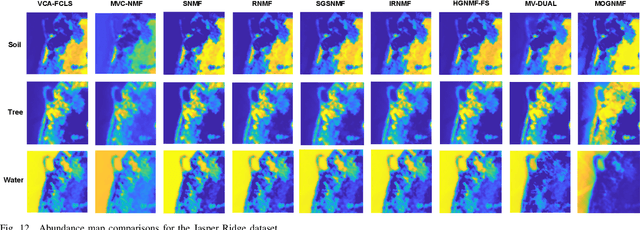
Hyperspectral unmixing (HU) is a critical yet challenging task in remote sensing. However, existing nonnegative matrix factorization (NMF) methods with graph learning mostly focus on first-order or second-order nearest neighbor relationships and usually require manual parameter tuning, which fails to characterize intrinsic data structures. To address the above issues, we propose a novel adaptive multi-order graph regularized NMF method (MOGNMF) with three key features. First, multi-order graph regularization is introduced into the NMF framework to exploit global and local information comprehensively. Second, these parameters associated with the multi-order graph are learned adaptively through a data-driven approach. Third, dual sparsity is embedded to obtain better robustness, i.e., $\ell_{1/2}$-norm on the abundance matrix and $\ell_{2,1}$-norm on the noise matrix. To solve the proposed model, we develop an alternating minimization algorithm whose subproblems have explicit solutions, thus ensuring effectiveness. Experiments on simulated and real hyperspectral data indicate that the proposed method delivers better unmixing results.

Tuning-Free Structured Sparse PCA via Deep Unfolding Networks

Sparse principal component analysis (PCA) is a well-established dimensionality reduction technique that is often used for unsupervised feature selection (UFS). However, determining the regularization parameters is rather challenging, and conventional approaches, including grid search and Bayesian optimization, not only bring great computational costs but also exhibit high sensitivity. To address these limitations, we first establish a structured sparse PCA formulation by integrating $\ell_1$-norm and $\ell_{2,1}$-norm to capture the local and global structures, respectively. Building upon the off-the-shelf alternating direction method of multipliers (ADMM) optimization framework, we then design an interpretable deep unfolding network that translates iterative optimization steps into trainable neural architectures. This innovation enables automatic learning of the regularization parameters, effectively bypassing the empirical tuning requirements of conventional methods. Numerical experiments on benchmark datasets validate the advantages of our proposed method over the existing state-of-the-art methods. Our code will be accessible at https://github.com/xianchaoxiu/SPCA-Net.

Enhancing Unsupervised Feature Selection via Double Sparsity Constrained Optimization

Unsupervised feature selection (UFS) is widely applied in machine learning and pattern recognition. However, most of the existing methods only consider a single sparsity, which makes it difficult to select valuable and discriminative feature subsets from the original high-dimensional feature set. In this paper, we propose a new UFS method called DSCOFS via embedding double sparsity constrained optimization into the classical principal component analysis (PCA) framework. Double sparsity refers to using $\ell_{2,0}$-norm and $\ell_0$-norm to simultaneously constrain variables, by adding the sparsity of different types, to achieve the purpose of improving the accuracy of identifying differential features. The core is that $\ell_{2,0}$-norm can remove irrelevant and redundant features, while $\ell_0$-norm can filter out irregular noisy features, thereby complementing $\ell_{2,0}$-norm to improve discrimination. An effective proximal alternating minimization method is proposed to solve the resulting nonconvex nonsmooth model. Theoretically, we rigorously prove that the sequence generated by our method globally converges to a stationary point. Numerical experiments on three synthetic datasets and eight real-world datasets demonstrate the effectiveness, stability, and convergence of the proposed method. In particular, the average clustering accuracy (ACC) and normalized mutual information (NMI) are improved by at least 3.34% and 3.02%, respectively, compared with the state-of-the-art methods. More importantly, two common statistical tests and a new feature similarity metric verify the advantages of double sparsity. All results suggest that our proposed DSCOFS provides a new perspective for feature selection.