DisGNet: A Distance Graph Neural Network for Forward Kinematics Learning of Gough-Stewart Platform

In this paper, we propose a graph neural network, DisGNet, for learning the graph distance matrix to address the forward kinematics problem of the Gough-Stewart platform. DisGNet employs the k-FWL algorithm for message-passing, providing high expressiveness with a small parameter count, making it suitable for practical deployment. Additionally, we introduce the GPU-friendly Newton-Raphson method, an efficient parallelized optimization method executed on the GPU to refine DisGNet's output poses, achieving ultra-high-precision pose. This novel two-stage approach delivers ultra-high precision output while meeting real-time requirements. Our results indicate that on our dataset, DisGNet can achieves error accuracys below 1mm and 1deg at 79.8\% and 98.2\%, respectively. As executed on a GPU, our two-stage method can ensure the requirement for real-time computation. Codes are released at https://github.com/FLAMEZZ5201/DisGNet.

Conditional Stochastic Interpolation for Generative Learning

We propose a conditional stochastic interpolation (CSI) approach to learning conditional distributions. CSI learns probability flow equations or stochastic differential equations that transport a reference distribution to the target conditional distribution. This is achieved by first learning the drift function and the conditional score function based on conditional stochastic interpolation, which are then used to construct a deterministic process governed by an ordinary differential equation or a diffusion process for conditional sampling. In our proposed CSI model, we incorporate an adaptive diffusion term to address the instability issues arising during the training process. We provide explicit forms of the conditional score function and the drift function in terms of conditional expectations under mild conditions, which naturally lead to an nonparametric regression approach to estimating these functions. Furthermore, we establish non-asymptotic error bounds for learning the target conditional distribution via conditional stochastic interpolation in terms of KL divergence, taking into account the neural network approximation error. We illustrate the application of CSI on image generation using a benchmark image dataset.

Gaussian Interpolation Flows

Gaussian denoising has emerged as a powerful principle for constructing simulation-free continuous normalizing flows for generative modeling. Despite their empirical successes, theoretical properties of these flows and the regularizing effect of Gaussian denoising have remained largely unexplored. In this work, we aim to address this gap by investigating the well-posedness of simulation-free continuous normalizing flows built on Gaussian denoising. Through a unified framework termed Gaussian interpolation flow, we establish the Lipschitz regularity of the flow velocity field, the existence and uniqueness of the flow, and the Lipschitz continuity of the flow map and the time-reversed flow map for several rich classes of target distributions. This analysis also sheds light on the auto-encoding and cycle-consistency properties of Gaussian interpolation flows. Additionally, we delve into the stability of these flows in source distributions and perturbations of the velocity field, using the quadratic Wasserstein distance as a metric. Our findings offer valuable insights into the learning techniques employed in Gaussian interpolation flows for generative modeling, providing a solid theoretical foundation for end-to-end error analyses of learning GIFs with empirical observations.

DEFN: Dual-Encoder Fourier Group Harmonics Network for Three-Dimensional Macular Hole Reconstruction with Stochastic Retinal Defect Augmentation and Dynamic Weight Composition

The spatial and quantitative parameters of macular holes are vital for diagnosis, surgical choices, and post-op monitoring. Macular hole diagnosis and treatment rely heavily on spatial and quantitative data, yet the scarcity of such data has impeded the progress of deep learning techniques for effective segmentation and real-time 3D reconstruction. To address this challenge, we assembled the world's largest macular hole dataset, Retinal OCTfor Macular Hole Enhancement (ROME-3914), and a Comprehensive Archive for Retinal Segmentation (CARS-30k), both expertly annotated. In addition, we developed an innovative 3D segmentation network, the Dual-Encoder FuGH Network (DEFN), which integrates three innovative modules: Fourier Group Harmonics (FuGH), Simplified 3D Spatial Attention (S3DSA) and Harmonic Squeeze-and-Excitation Module (HSE). These three modules synergistically filter noise, reduce computational complexity, emphasize detailed features, and enhance the network's representation ability. We also proposed a novel data augmentation method, Stochastic Retinal Defect Injection (SRDI), and a network optimization strategy DynamicWeightCompose (DWC), to further improve the performance of DEFN. Compared with 13 baselines, our DEFN shows the best performance. We also offer precise 3D retinal reconstruction and quantitative metrics, bringing revolutionary diagnostic and therapeutic decision-making tools for ophthalmologists, and is expected to completely reshape the diagnosis and treatment patterns of difficult-to-treat macular degeneration. The source code is publicly available at: https://github.com/IIPL-HangzhouDianUniversity/DEFN-Pytorch.

G10: Enabling An Efficient Unified GPU Memory and Storage Architecture with Smart Tensor Migrations

To break the GPU memory wall for scaling deep learning workloads, a variety of architecture and system techniques have been proposed recently. Their typical approaches include memory extension with flash memory and direct storage access. However, these techniques still suffer from suboptimal performance and introduce complexity to the GPU memory management, making them hard to meet the scalability requirement of deep learning workloads today. In this paper, we present a unified GPU memory and storage architecture named G10 driven by the fact that the tensor behaviors of deep learning workloads are highly predictable. G10 integrates the host memory, GPU memory, and flash memory into a unified memory space, to scale the GPU memory capacity while enabling transparent data migrations. Based on this unified GPU memory and storage architecture, G10 utilizes compiler techniques to characterize the tensor behaviors in deep learning workloads. Therefore, it can schedule data migrations in advance by considering the available bandwidth of flash memory and host memory. The cooperative mechanism between deep learning compilers and the unified memory architecture enables G10 to hide data transfer overheads in a transparent manner. We implement G10 based on an open-source GPU simulator. Our experiments demonstrate that G10 outperforms state-of-the-art GPU memory solutions by up to 1.75$\times$, without code modifications to deep learning workloads. With the smart data migration mechanism, G10 can reach 90.3\% of the performance of the ideal case assuming unlimited GPU memory.

Non-Asymptotic Bounds for Adversarial Excess Risk under Misspecified Models

We propose a general approach to evaluating the performance of robust estimators based on adversarial losses under misspecified models. We first show that adversarial risk is equivalent to the risk induced by a distributional adversarial attack under certain smoothness conditions. This ensures that the adversarial training procedure is well-defined. To evaluate the generalization performance of the adversarial estimator, we study the adversarial excess risk. Our proposed analysis method includes investigations on both generalization error and approximation error. We then establish non-asymptotic upper bounds for the adversarial excess risk associated with Lipschitz loss functions. In addition, we apply our general results to adversarial training for classification and regression problems. For the quadratic loss in nonparametric regression, we show that the adversarial excess risk bound can be improved over those for a general loss.

Wasserstein Generative Regression

In this paper, we propose a new and unified approach for nonparametric regression and conditional distribution learning. Our approach simultaneously estimates a regression function and a conditional generator using a generative learning framework, where a conditional generator is a function that can generate samples from a conditional distribution. The main idea is to estimate a conditional generator that satisfies the constraint that it produces a good regression function estimator. We use deep neural networks to model the conditional generator. Our approach can handle problems with multivariate outcomes and covariates, and can be used to construct prediction intervals. We provide theoretical guarantees by deriving non-asymptotic error bounds and the distributional consistency of our approach under suitable assumptions. We also perform numerical experiments with simulated and real data to demonstrate the effectiveness and superiority of our approach over some existing approaches in various scenarios.

Differentiable Neural Networks with RePU Activation: with Applications to Score Estimation and Isotonic Regression

We study the properties of differentiable neural networks activated by rectified power unit (RePU) functions. We show that the partial derivatives of RePU neural networks can be represented by RePUs mixed-activated networks and derive upper bounds for the complexity of the function class of derivatives of RePUs networks. We establish error bounds for simultaneously approximating $C^s$ smooth functions and their derivatives using RePU-activated deep neural networks. Furthermore, we derive improved approximation error bounds when data has an approximate low-dimensional support, demonstrating the ability of RePU networks to mitigate the curse of dimensionality. To illustrate the usefulness of our results, we consider a deep score matching estimator (DSME) and propose a penalized deep isotonic regression (PDIR) using RePU networks. We establish non-asymptotic excess risk bounds for DSME and PDIR under the assumption that the target functions belong to a class of $C^s$ smooth functions. We also show that PDIR has a robustness property in the sense it is consistent with vanishing penalty parameters even when the monotonicity assumption is not satisfied. Furthermore, if the data distribution is supported on an approximate low-dimensional manifold, we show that DSME and PDIR can mitigate the curse of dimensionality.

CREPES: Cooperative RElative Pose EStimation towards Real-World Multi-Robot Systems

Mutual localization plays a crucial role in multi-robot systems. In this work, we propose a novel system to estimate the 3D relative pose targeting real-world applications. We design and implement a compact hardware module using active infrared (IR) LEDs, an IR fish-eye camera, an ultra-wideband (UWB) module and an inertial measurement unit (IMU). By leveraging IR light communication, the system solves data association between visual detection and UWB ranging. Ranging measurements from the UWB and directional information from the camera offer relative 3D position estimation. Combining the mutual relative position with neighbors and the gravity constraints provided by IMUs, we can estimate the 3D relative pose from every single frame of sensor fusion. In addition, we design an estimator based on the error-state Kalman filter (ESKF) to enhance system accuracy and robustness. When multiple neighbors are available, a Pose Graph Optimization (PGO) algorithm is applied to further improve system accuracy. We conduct experiments in various environments, and the results show that our system outperforms state-of-the-art accuracy and robustness, especially in challenging environments.

Nonparametric Quantile Regression: Non-Crossing Constraints and Conformal Prediction

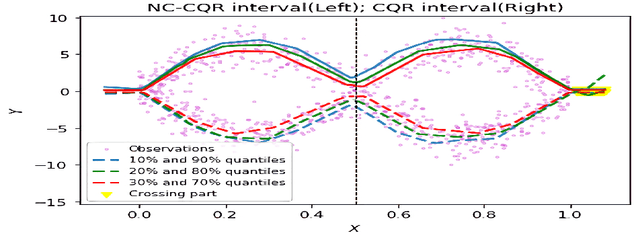
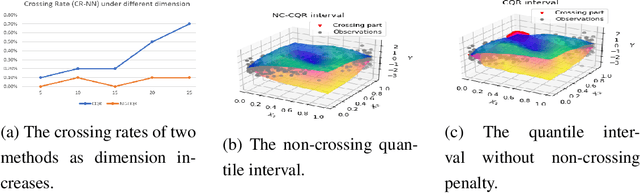
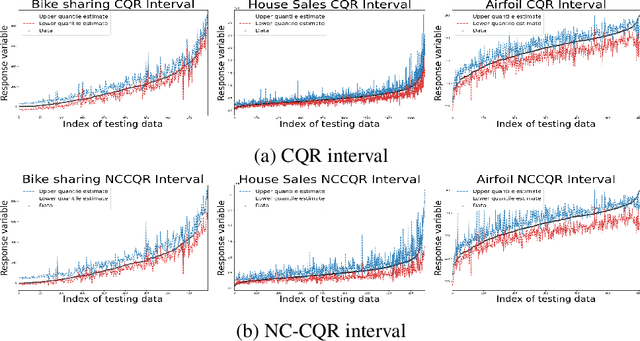
We propose a nonparametric quantile regression method using deep neural networks with a rectified linear unit penalty function to avoid quantile crossing. This penalty function is computationally feasible for enforcing non-crossing constraints in multi-dimensional nonparametric quantile regression. We establish non-asymptotic upper bounds for the excess risk of the proposed nonparametric quantile regression function estimators. Our error bounds achieve optimal minimax rate of convergence for the Holder class, and the prefactors of the error bounds depend polynomially on the dimension of the predictor, instead of exponentially. Based on the proposed non-crossing penalized deep quantile regression, we construct conformal prediction intervals that are fully adaptive to heterogeneity. The proposed prediction interval is shown to have good properties in terms of validity and accuracy under reasonable conditions. We also derive non-asymptotic upper bounds for the difference of the lengths between the proposed non-crossing conformal prediction interval and the theoretically oracle prediction interval. Numerical experiments including simulation studies and a real data example are conducted to demonstrate the effectiveness of the proposed method.