A PAC-Bayesian approach to generalization for quantum models

Generalization is a central concept in machine learning theory, yet for quantum models, it is predominantly analyzed through uniform bounds that depend on a model's overall capacity rather than the specific function learned. These capacity-based uniform bounds are often too loose and entirely insensitive to the actual training and learning process. Previous theoretical guarantees have failed to provide non-uniform, data-dependent bounds that reflect the specific properties of the learned solution rather than the worst-case behavior of the entire hypothesis class. To address this limitation, we derive the first PAC-Bayesian generalization bounds for a broad class of quantum models by analyzing layered circuits composed of general quantum channels, which include dissipative operations such as mid-circuit measurements and feedforward. Through a channel perturbation analysis, we establish non-uniform bounds that depend on the norms of learned parameter matrices; we extend these results to symmetry-constrained equivariant quantum models; and we validate our theoretical framework with numerical experiments. This work provides actionable model design insights and establishes a foundational tool for a more nuanced understanding of generalization in quantum machine learning.

Prospects for quantum advantage in machine learning from the representability of functions

Demonstrating quantum advantage in machine learning tasks requires navigating a complex landscape of proposed models and algorithms. To bring clarity to this search, we introduce a framework that connects the structure of parametrized quantum circuits to the mathematical nature of the functions they can actually learn. Within this framework, we show how fundamental properties, like circuit depth and non-Clifford gate count, directly determine whether a model's output leads to efficient classical simulation or surrogation. We argue that this analysis uncovers common pathways to dequantization that underlie many existing simulation methods. More importantly, it reveals critical distinctions between models that are fully simulatable, those whose function space is classically tractable, and those that remain robustly quantum. This perspective provides a conceptual map of this landscape, clarifying how different models relate to classical simulability and pointing to where opportunities for quantum advantage may lie.

Artificial intelligence for representing and characterizing quantum systems

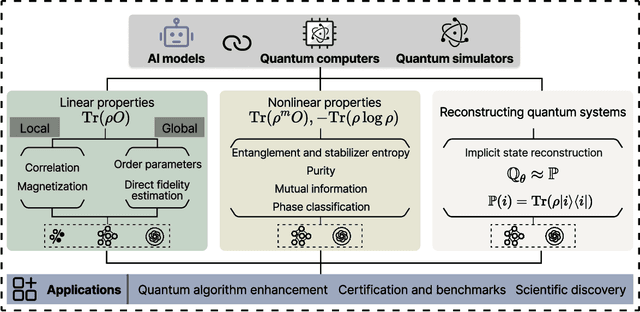
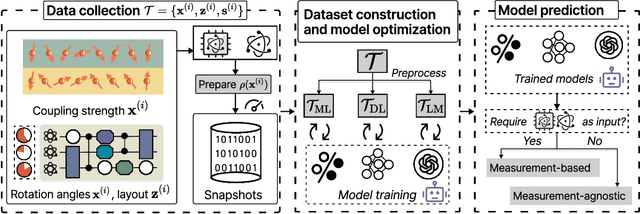
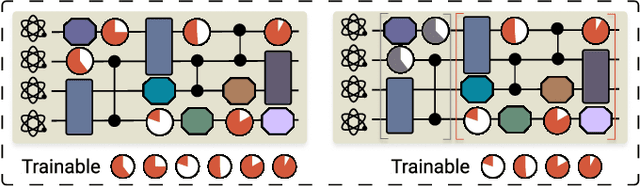
Efficient characterization of large-scale quantum systems, especially those produced by quantum analog simulators and megaquop quantum computers, poses a central challenge in quantum science due to the exponential scaling of the Hilbert space with respect to system size. Recent advances in artificial intelligence (AI), with its aptitude for high-dimensional pattern recognition and function approximation, have emerged as a powerful tool to address this challenge. A growing body of research has leveraged AI to represent and characterize scalable quantum systems, spanning from theoretical foundations to experimental realizations. Depending on how prior knowledge and learning architectures are incorporated, the integration of AI into quantum system characterization can be categorized into three synergistic paradigms: machine learning, and, in particular, deep learning and language models. This review discusses how each of these AI paradigms contributes to two core tasks in quantum systems characterization: quantum property prediction and the construction of surrogates for quantum states. These tasks underlie diverse applications, from quantum certification and benchmarking to the enhancement of quantum algorithms and the understanding of strongly correlated phases of matter. Key challenges and open questions are also discussed, together with future prospects at the interface of AI and quantum science.

Quantum computing and artificial intelligence: status and perspectives

This white paper discusses and explores the various points of intersection between quantum computing and artificial intelligence (AI). It describes how quantum computing could support the development of innovative AI solutions. It also examines use cases of classical AI that can empower research and development in quantum technologies, with a focus on quantum computing and quantum sensing. The purpose of this white paper is to provide a long-term research agenda aimed at addressing foundational questions about how AI and quantum computing interact and benefit one another. It concludes with a set of recommendations and challenges, including how to orchestrate the proposed theoretical work, align quantum AI developments with quantum hardware roadmaps, estimate both classical and quantum resources - especially with the goal of mitigating and optimizing energy consumption - advance this emerging hybrid software engineering discipline, and enhance European industrial competitiveness while considering societal implications.

Towards efficient quantum algorithms for diffusion probability models

A diffusion probabilistic model (DPM) is a generative model renowned for its ability to produce high-quality outputs in tasks such as image and audio generation. However, training DPMs on large, high-dimensional datasets such as high-resolution images or audio incurs significant computational, energy, and hardware costs. In this work, we introduce efficient quantum algorithms for implementing DPMs through various quantum ODE solvers. These algorithms highlight the potential of quantum Carleman linearization for diverse mathematical structures, leveraging state-of-the-art quantum linear system solvers (QLSS) or linear combination of Hamiltonian simulations (LCHS). Specifically, we focus on two approaches: DPM-solver-$k$ which employs exact $k$-th order derivatives to compute a polynomial approximation of $\epsilon_\theta(x_\lambda,\lambda)$; and UniPC which uses finite difference of $\epsilon_\theta(x_\lambda,\lambda)$ at different points $(x_{s_m}, \lambda_{s_m})$ to approximate higher-order derivatives. As such, this work represents one of the most direct and pragmatic applications of quantum algorithms to large-scale machine learning models, presumably talking substantial steps towards demonstrating the practical utility of quantum computing.

Opportunities and limitations of explaining quantum machine learning

A common trait of many machine learning models is that it is often difficult to understand and explain what caused the model to produce the given output. While the explainability of neural networks has been an active field of research in the last years, comparably little is known for quantum machine learning models. Despite a few recent works analyzing some specific aspects of explainability, as of now there is no clear big picture perspective as to what can be expected from quantum learning models in terms of explainability. In this work, we address this issue by identifying promising research avenues in this direction and lining out the expected future results. We additionally propose two explanation methods designed specifically for quantum machine learning models, as first of their kind to the best of our knowledge. Next to our pre-view of the field, we compare both existing and novel methods to explain the predictions of quantum learning models. By studying explainability in quantum machine learning, we can contribute to the sustainable development of the field, preventing trust issues in the future.

Interactive proofs for verifying (quantum) learning and testing

We consider the problem of testing and learning from data in the presence of resource constraints, such as limited memory or weak data access, which place limitations on the efficiency and feasibility of testing or learning. In particular, we ask the following question: Could a resource-constrained learner/tester use interaction with a resource-unconstrained but untrusted party to solve a learning or testing problem more efficiently than they could without such an interaction? In this work, we answer this question both abstractly and for concrete problems, in two complementary ways: For a wide variety of scenarios, we prove that a resource-constrained learner cannot gain any advantage through classical interaction with an untrusted prover. As a special case, we show that for the vast majority of testing and learning problems in which quantum memory is a meaningful resource, a memory-constrained quantum algorithm cannot overcome its limitations via classical communication with a memory-unconstrained quantum prover. In contrast, when quantum communication is allowed, we construct a variety of interactive proof protocols, for specific learning and testing problems, which allow memory-constrained quantum verifiers to gain significant advantages through delegation to untrusted provers. These results highlight both the limitations and potential of delegating learning and testing problems to resource-rich but untrusted third parties.

Artificially intelligent Maxwell's demon for optimal control of open quantum systems

Feedback control of open quantum systems is of fundamental importance for practical applications in various contexts, ranging from quantum computation to quantum error correction and quantum metrology. Its use in the context of thermodynamics further enables the study of the interplay between information and energy. However, deriving optimal feedback control strategies is highly challenging, as it involves the optimal control of open quantum systems, the stochastic nature of quantum measurement, and the inclusion of policies that maximize a long-term time- and trajectory-averaged goal. In this work, we employ a reinforcement learning approach to automate and capture the role of a quantum Maxwell's demon: the agent takes the literal role of discovering optimal feedback control strategies in qubit-based systems that maximize a trade-off between measurement-powered cooling and measurement efficiency. Considering weak or projective quantum measurements, we explore different regimes based on the ordering between the thermalization, the measurement, and the unitary feedback timescales, finding different and highly non-intuitive, yet interpretable, strategies. In the thermalization-dominated regime, we find strategies with elaborate finite-time thermalization protocols conditioned on measurement outcomes. In the measurement-dominated regime, we find that optimal strategies involve adaptively measuring different qubit observables reflecting the acquired information, and repeating multiple weak measurements until the quantum state is "sufficiently pure", leading to random walks in state space. Finally, we study the case when all timescales are comparable, finding new feedback control strategies that considerably outperform more intuitive ones. We discuss a two-qubit example where we explore the role of entanglement and conclude discussing the scaling of our results to quantum many-body systems.

Online learning of quantum processes

Among recent insights into learning quantum states, online learning and shadow tomography procedures are notable for their ability to accurately predict expectation values even of adaptively chosen observables. In contrast to the state case, quantum process learning tasks with a similarly adaptive nature have received little attention. In this work, we investigate online learning tasks for quantum processes. Whereas online learning is infeasible for general quantum channels, we show that channels of bounded gate complexity as well as Pauli channels can be online learned in the regret and mistake-bounded models of online learning. In fact, we can online learn probabilistic mixtures of any exponentially large set of known channels. We also provide a provably sample-efficient shadow tomography procedure for Pauli channels. Our results extend beyond quantum channels to non-Markovian multi-time processes, with favorable regret and mistake bounds, as well as a shadow tomography procedure. We complement our online learning upper bounds with mistake as well as computational lower bounds. On the technical side, we make use of the multiplicative weights update algorithm, classical adaptive data analysis, and Bell sampling, as well as tools from the theory of quantum combs for multi-time quantum processes. Our work initiates a study of online learning for classes of quantum channels and, more generally, non-Markovian quantum processes. Given the importance of online learning for state shadow tomography, this may serve as a step towards quantum channel variants of adaptive shadow tomography.

Learning topological states from randomized measurements using variational tensor network tomography

Learning faithful representations of quantum states is crucial to fully characterizing the variety of many-body states created on quantum processors. While various tomographic methods such as classical shadow and MPS tomography have shown promise in characterizing a wide class of quantum states, they face unique limitations in detecting topologically ordered two-dimensional states. To address this problem, we implement and study a heuristic tomographic method that combines variational optimization on tensor networks with randomized measurement techniques. Using this approach, we demonstrate its ability to learn the ground state of the surface code Hamiltonian as well as an experimentally realizable quantum spin liquid state. In particular, we perform numerical experiments using MPS ans\"atze and systematically investigate the sample complexity required to achieve high fidelities for systems of sizes up to $48$ qubits. In addition, we provide theoretical insights into the scaling of our learning algorithm by analyzing the statistical properties of maximum likelihood estimation. Notably, our method is sample-efficient and experimentally friendly, only requiring snapshots of the quantum state measured randomly in the $X$ or $Z$ bases. Using this subset of measurements, our approach can effectively learn any real pure states represented by tensor networks, and we rigorously prove that random-$XZ$ measurements are tomographically complete for such states.