Potential and limitations of random Fourier features for dequantizing quantum machine learning

Quantum machine learning is arguably one of the most explored applications of near-term quantum devices. Much focus has been put on notions of variational quantum machine learning where parameterized quantum circuits (PQCs) are used as learning models. These PQC models have a rich structure which suggests that they might be amenable to efficient dequantization via random Fourier features (RFF). In this work, we establish necessary and sufficient conditions under which RFF does indeed provide an efficient dequantization of variational quantum machine learning for regression. We build on these insights to make concrete suggestions for PQC architecture design, and to identify structures which are necessary for a regression problem to admit a potential quantum advantage via PQC based optimization.

Classical surrogates for quantum learning models

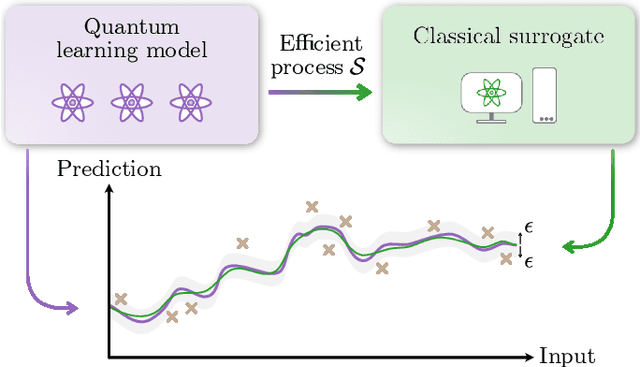
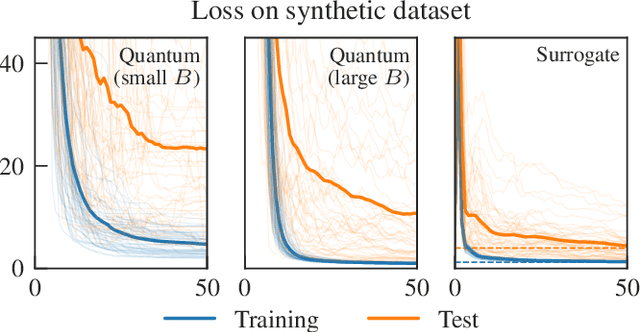
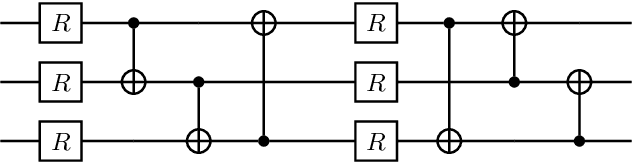
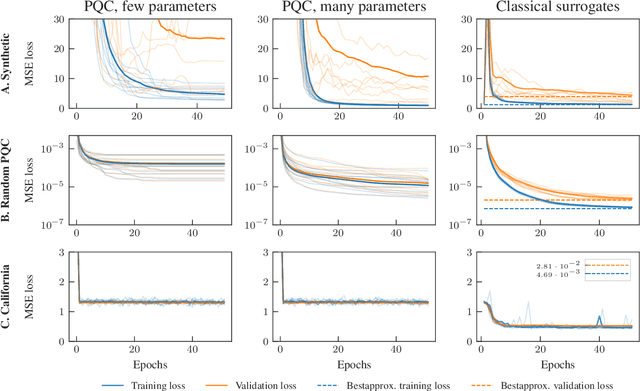
The advent of noisy intermediate-scale quantum computers has put the search for possible applications to the forefront of quantum information science. One area where hopes for an advantage through near-term quantum computers are high is quantum machine learning, where variational quantum learning models based on parametrized quantum circuits are discussed. In this work, we introduce the concept of a classical surrogate, a classical model which can be efficiently obtained from a trained quantum learning model and reproduces its input-output relations. As inference can be performed classically, the existence of a classical surrogate greatly enhances the applicability of a quantum learning strategy. However, the classical surrogate also challenges possible advantages of quantum schemes. As it is possible to directly optimize the ansatz of the classical surrogate, they create a natural benchmark the quantum model has to outperform. We show that large classes of well-analyzed re-uploading models have a classical surrogate. We conducted numerical experiments and found that these quantum models show no advantage in performance or trainability in the problems we analyze. This leaves only generalization capability as possible point of quantum advantage and emphasizes the dire need for a better understanding of inductive biases of quantum learning models.

Exploiting symmetry in variational quantum machine learning

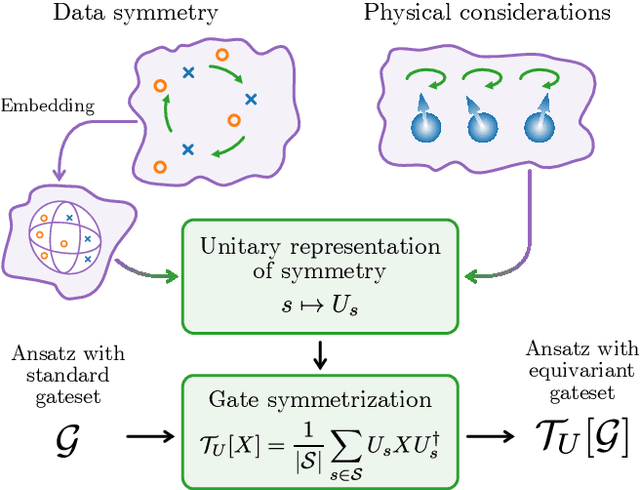
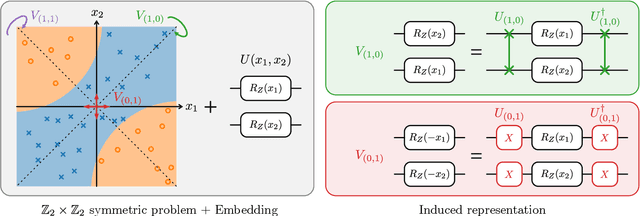
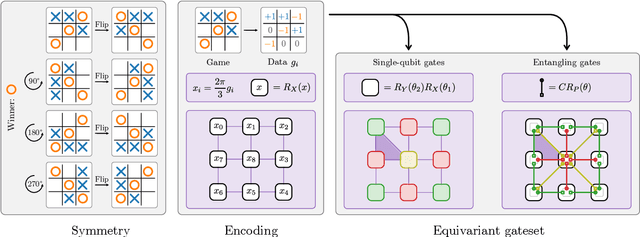
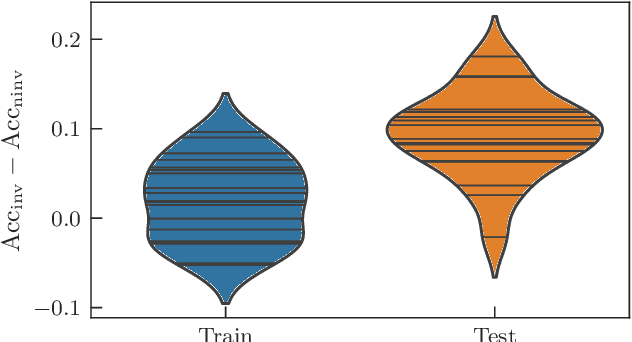
Variational quantum machine learning is an extensively studied application of near-term quantum computers. The success of variational quantum learning models crucially depends on finding a suitable parametrization of the model that encodes an inductive bias relevant to the learning task. However, precious little is known about guiding principles for the construction of suitable parametrizations. In this work, we holistically explore when and how symmetries of the learning problem can be exploited to construct quantum learning models with outcomes invariant under the symmetry of the learning task. Building on tools from representation theory, we show how a standard gateset can be transformed into an equivariant gateset that respects the symmetries of the problem at hand through a process of gate symmetrization. We benchmark the proposed methods on two toy problems that feature a non-trivial symmetry and observe a substantial increase in generalization performance. As our tools can also be applied in a straightforward way to other variational problems with symmetric structure, we show how equivariant gatesets can be used in variational quantum eigensolvers.

Encoding-dependent generalization bounds for parametrized quantum circuits

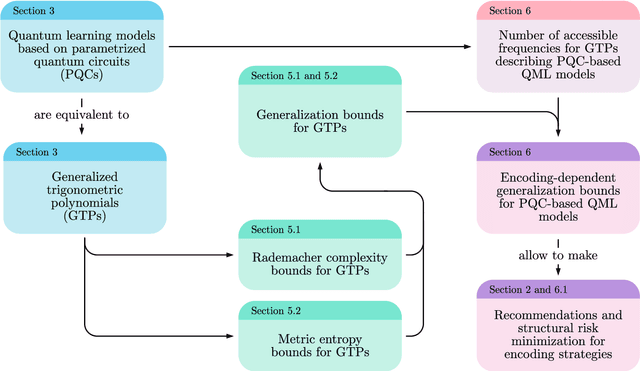
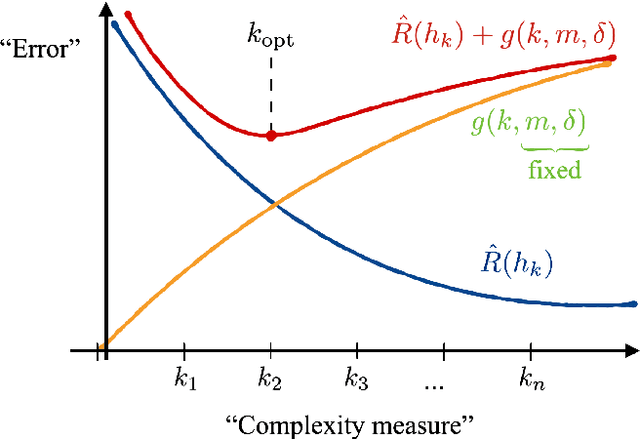
A large body of recent work has begun to explore the potential of parametrized quantum circuits (PQCs) as machine learning models, within the framework of hybrid quantum-classical optimization. In particular, theoretical guarantees on the out-of-sample performance of such models, in terms of generalization bounds, have emerged. However, none of these generalization bounds depend explicitly on how the classical input data is encoded into the PQC. We derive generalization bounds for PQC-based models that depend explicitly on the strategy used for data-encoding. These imply bounds on the performance of trained PQC-based models on unseen data. Moreover, our results facilitate the selection of optimal data-encoding strategies via structural risk minimization, a mathematically rigorous framework for model selection. We obtain our generalization bounds by bounding the complexity of PQC-based models as measured by the Rademacher complexity and the metric entropy, two complexity measures from statistical learning theory. To achieve this, we rely on a representation of PQC-based models via trigonometric functions. Our generalization bounds emphasize the importance of well-considered data-encoding strategies for PQC-based models.

Training Quantum Embedding Kernels on Near-Term Quantum Computers

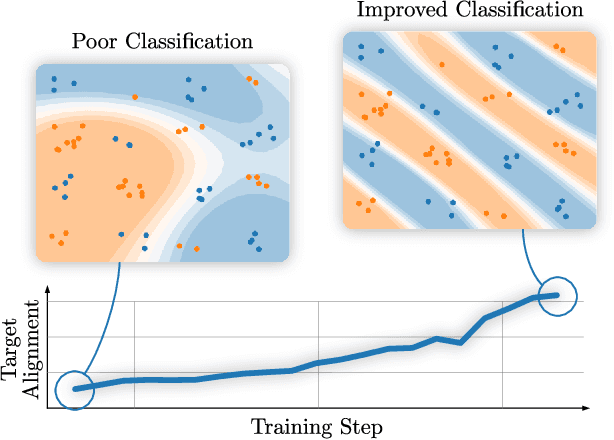
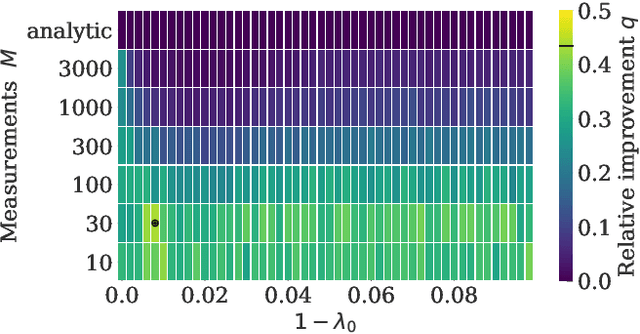
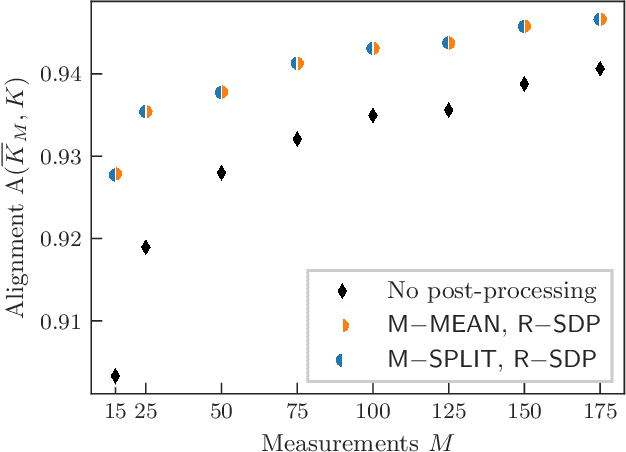
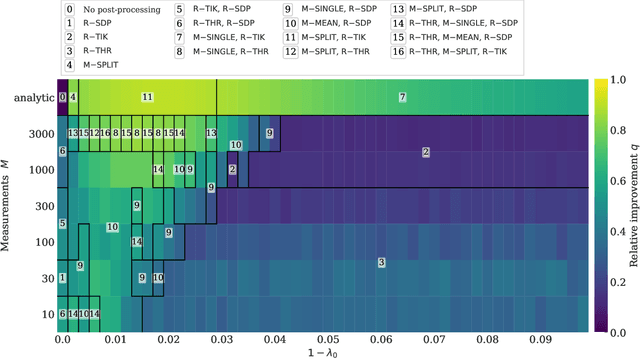
Kernel methods are a cornerstone of classical machine learning. The idea of using quantum computers to compute kernels has recently attracted attention. Quantum embedding kernels (QEKs) constructed by embedding data into the Hilbert space of a quantum computer are a particular quantum kernel technique that allows to gather insights into learning problems and that are particularly suitable for noisy intermediate-scale quantum devices. In this work, we first provide an accessible introduction to quantum embedding kernels and then analyze the practical issues arising when realizing them on a noisy near-term quantum computer. We focus on quantum embedding kernels with variational parameters. These variational parameters are optimized for a given dataset by increasing the kernel-target alignment, a heuristic connected to the achievable classification accuracy. We further show under which conditions noise from device imperfections influences the predicted kernel and provide a strategy to mitigate these detrimental effects which is tailored to quantum embedding kernels. We also address the influence of finite sampling and derive bounds that put guarantees on the quality of the kernel matrix. We illustrate our findings by numerical experiments and tests on actual hardware.

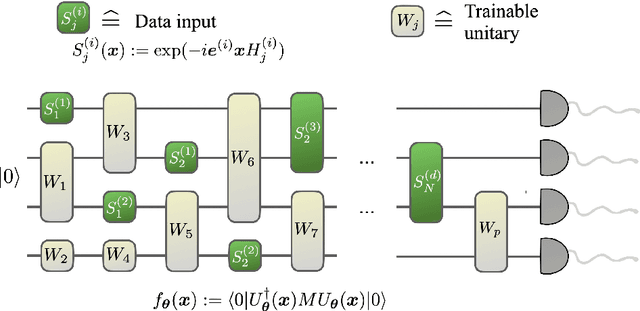
The effect of data encoding on the expressive power of variational quantum machine learning models

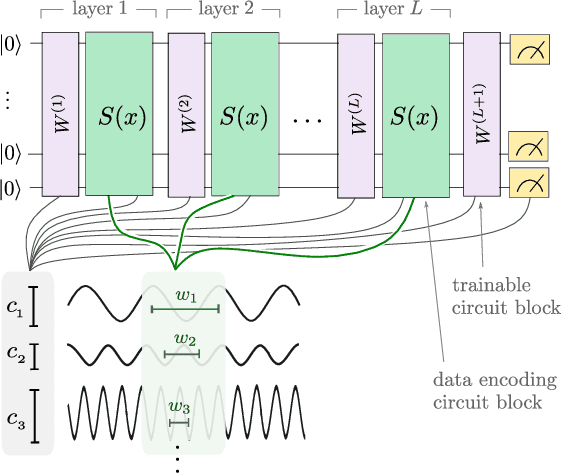
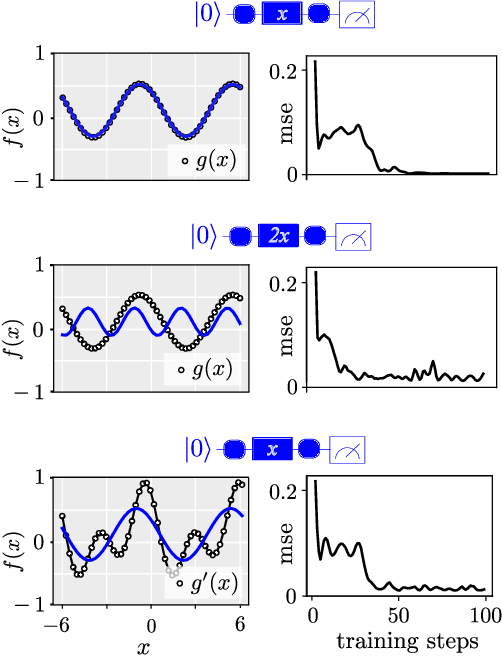
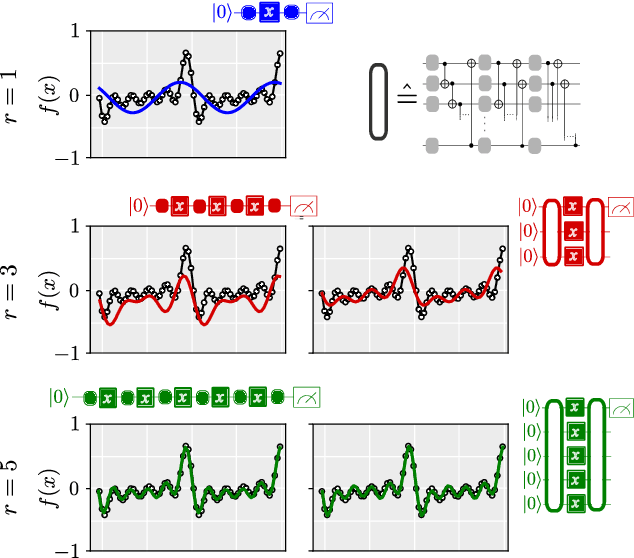
Quantum computers can be used for supervised learning by treating parametrised quantum circuits as models that map data inputs to predictions. While a lot of work has been done to investigate practical implications of this approach, many important theoretical properties of these models remain unknown. Here we investigate how the strategy with which data is encoded into the model influences the expressive power of parametrised quantum circuits as function approximators. We show that one can naturally write a quantum model as a partial Fourier series in the data, where the accessible frequencies are determined by the nature of the data encoding gates in the circuit. By repeating simple data encoding gates multiple times, quantum models can access increasingly rich frequency spectra. We show that there exist quantum models which can realise all possible sets of Fourier coefficients, and therefore, if the accessible frequency spectrum is asymptotically rich enough, such models are universal function approximators.