Few measurement shots challenge generalization in learning to classify entanglement

The ability to extract general laws from a few known examples depends on the complexity of the problem and on the amount of training data. In the quantum setting, the learner's generalization performance is further challenged by the destructive nature of quantum measurements that, together with the no-cloning theorem, limits the amount of information that can be extracted from each training sample. In this paper we focus on hybrid quantum learning techniques where classical machine-learning methods are paired with quantum algorithms and show that, in some settings, the uncertainty coming from a few measurement shots can be the dominant source of errors. We identify an instance of this possibly general issue by focusing on the classification of maximally entangled vs. separable states, showing that this toy problem becomes challenging for learners unaware of entanglement theory. Finally, we introduce an estimator based on classical shadows that performs better in the big data, few copy regime. Our results show that the naive application of classical machine-learning methods to the quantum setting is problematic, and that a better theoretical foundation of quantum learning is required.

Learning to Classify Quantum Phases of Matter with a Few Measurements

We study the identification of quantum phases of matter, at zero temperature, when only part of the phase diagram is known in advance. Following a supervised learning approach, we show how to use our previous knowledge to construct an observable capable of classifying the phase even in the unknown region. By using a combination of classical and quantum techniques, such as tensor networks, kernel methods, generalization bounds, quantum algorithms, and shadow estimators, we show that, in some cases, the certification of new ground states can be obtained with a polynomial number of measurements. An important application of our findings is the classification of the phases of matter obtained in quantum simulators, e.g., cold atom experiments, capable of efficiently preparing ground states of complex many-particle systems and applying simple measurements, e.g., single qubit measurements, but unable to perform a universal set of gates.

Quantum Adversarial Learning for Kernel Methods

We show that hybrid quantum classifiers based on quantum kernel methods and support vector machines are vulnerable against adversarial attacks, namely small engineered perturbations of the input data can deceive the classifier into predicting the wrong result. Nonetheless, we also show that simple defence strategies based on data augmentation with a few crafted perturbations can make the classifier robust against new attacks. Our results find applications in security-critical learning problems and in mitigating the effect of some forms of quantum noise, since the attacker can also be understood as part of the surrounding environment.

Accuracy vs Memory Advantage in the Quantum Simulation of Stochastic Processes

Many inference scenarios rely on extracting relevant information from known data in order to make future predictions. When the underlying stochastic process satisfies certain assumptions, there is a direct mapping between its exact classical and quantum simulators, with the latter asymptotically using less memory. Here we focus on studying whether such quantum advantage persists when those assumptions are not satisfied, and the model is doomed to have imperfect accuracy. By studying the trade-off between accuracy and memory requirements, we show that quantum models can reach the same accuracy with less memory, or alternatively, better accuracy with the same memory. Finally, we discuss the implications of this result for learning tasks.

Statistical Complexity of Quantum Learning

Recent years have seen significant activity on the problem of using data for the purpose of learning properties of quantum systems or of processing classical or quantum data via quantum computing. As in classical learning, quantum learning problems involve settings in which the mechanism generating the data is unknown, and the main goal of a learning algorithm is to ensure satisfactory accuracy levels when only given access to data and, possibly, side information such as expert knowledge. This article reviews the complexity of quantum learning using information-theoretic techniques by focusing on data complexity, copy complexity, and model complexity. Copy complexity arises from the destructive nature of quantum measurements, which irreversibly alter the state to be processed, limiting the information that can be extracted about quantum data. For example, in a quantum system, unlike in classical machine learning, it is generally not possible to evaluate the training loss simultaneously on multiple hypotheses using the same quantum data. To make the paper self-contained and approachable by different research communities, we provide extensive background material on classical results from statistical learning theory, as well as on the distinguishability of quantum states. Throughout, we highlight the differences between quantum and classical learning by addressing both supervised and unsupervised learning, and we provide extensive pointers to the literature.

Time-Warping Invariant Quantum Recurrent Neural Networks via Quantum-Classical Adaptive Gating

Adaptive gating plays a key role in temporal data processing via classical recurrent neural networks (RNN), as it facilitates retention of past information necessary to predict the future, providing a mechanism that preserves invariance to time warping transformations. This paper builds on quantum recurrent neural networks (QRNNs), a dynamic model with quantum memory, to introduce a novel class of temporal data processing quantum models that preserve invariance to time-warping transformations of the (classical) input-output sequences. The model, referred to as time warping-invariant QRNN (TWI-QRNN), augments a QRNN with a quantum-classical adaptive gating mechanism that chooses whether to apply a parameterized unitary transformation at each time step as a function of the past samples of the input sequence via a classical recurrent model. The TWI-QRNN model class is derived from first principles, and its capacity to successfully implement time-warping transformations is experimentally demonstrated on examples with classical or quantum dynamics.

Online Convex Optimization of Programmable Quantum Computers to Simulate Time-Varying Quantum Channels

Simulating quantum channels is a fundamental primitive in quantum computing, since quantum channels define general (trace-preserving) quantum operations. An arbitrary quantum channel cannot be exactly simulated using a finite-dimensional programmable quantum processor, making it important to develop optimal approximate simulation techniques. In this paper, we study the challenging setting in which the channel to be simulated varies adversarially with time. We propose the use of matrix exponentiated gradient descent (MEGD), an online convex optimization method, and analytically show that it achieves a sublinear regret in time. Through experiments, we validate the main results for time-varying dephasing channels using a programmable generalized teleportation processor.

Generalization in Quantum Machine Learning: a Quantum Information Perspective

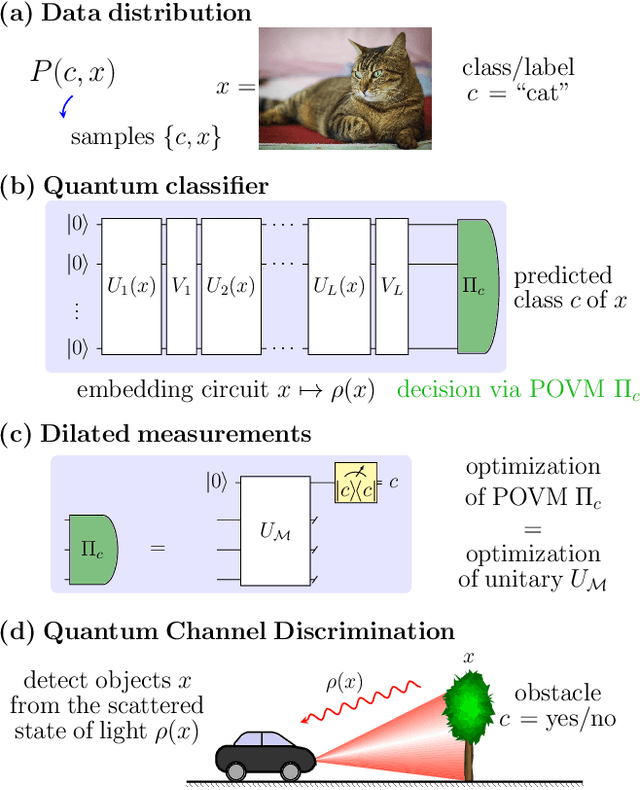
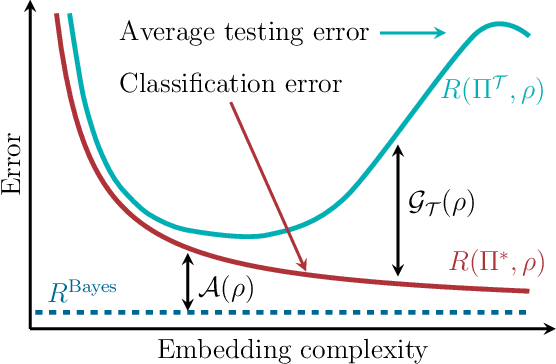
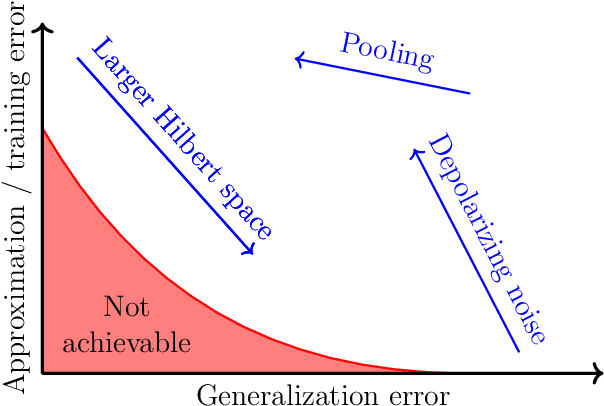
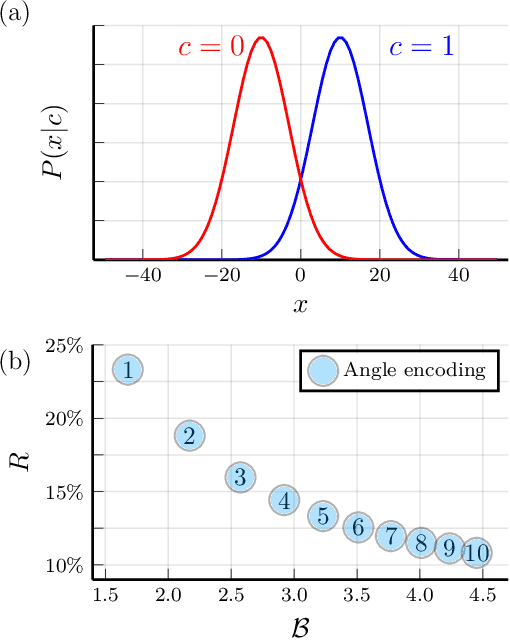
We study the machine learning problem of generalization when quantum operations are used to classify either classical data or quantum channels, where in both cases the task is to learn from data how to assign a certain class $c$ to inputs $x$ via measurements on a quantum state $\rho(x)$. A trained quantum model generalizes when it is able to predict the correct class for previously unseen data. We show that the accuracy and generalization capability of quantum classifiers depend on the (R\'enyi) mutual informations $I(C{:}Q)$ and $I_2(X{:}Q)$ between the quantum embedding $Q$ and the classical input space $X$ or class space $C$. Based on the above characterization, we then show how different properties of $Q$ affect classification accuracy and generalization, such as the dimension of the Hilbert space, the amount of noise, and the amount of neglected information via, e.g., pooling layers. Moreover, we introduce a quantum version of the Information Bottleneck principle that allows us to explore the various tradeoffs between accuracy and generalization.

Ultimate Limits of Thermal Imaging

Quantum Channel Discrimination (QCD) presents a fundamental task in quantum information theory, with critical applications in quantum reading, illumination, data-readout and more. The extension to multiple quantum channel discrimination has seen a recent focus to characterise potential quantum advantage associated with quantum enhanced discriminatory protocols. In this paper, we study thermal imaging as an environment localisation task, in which thermal images are modelled as ensembles of Gaussian phase insensitive channels with identical transmissivity, and pixels possess properties according to background (cold) or target (warm) thermal channels. Via the teleportation stretching of adaptive quantum protocols, we derive ultimate limits on the precision of pattern classification of abstract, binary thermal image spaces, and show that quantum enhanced strategies may be used to provide significant quantum advantage over known optimal classical strategies. The environmental conditions and necessary resources for which advantage may be obtained are studied and discussed. We then numerically investigate the use of quantum enhanced statistical classifiers, in which quantum sensors are used in conjunction with machine learning image classification methods. Proving definitive advantage in the low loss regime, this work motivates the use of quantum enhanced sources for short-range thermal imaging and detection techniques for future quantum technologies.

Quantum-enhanced barcode decoding and pattern recognition

Quantum hypothesis testing is one of the most fundamental problems in quantum information theory, with crucial implications in areas like quantum sensing, where it has been used to prove quantum advantage in a series of binary photonic protocols, e.g., for target detection or memory cell readout. In this work, we generalize this theoretical model to the multi-partite setting of barcode decoding and pattern recognition. We start by defining a digital image as an array or grid of pixels, each pixel corresponding to an ensemble of quantum channels. Specializing each pixel to a black and white alphabet, we naturally define an optical model of barcode. In this scenario, we show that the use of quantum entangled sources, combined with suitable measurements and data processing, greatly outperforms classical coherent-state strategies for the tasks of barcode data decoding and classification of black and white patterns. Moreover, introducing relevant bounds, we show that the problem of pattern recognition is significantly simpler than barcode decoding, as long as the minimum Hamming distance between images from different classes is large enough. Finally, we theoretically demonstrate the advantage of using quantum sensors for pattern recognition with the nearest neighbor classifier, a supervised learning algorithm, and numerically verify this prediction for handwritten digit classification.