Learning topological states from randomized measurements using variational tensor network tomography

Learning faithful representations of quantum states is crucial to fully characterizing the variety of many-body states created on quantum processors. While various tomographic methods such as classical shadow and MPS tomography have shown promise in characterizing a wide class of quantum states, they face unique limitations in detecting topologically ordered two-dimensional states. To address this problem, we implement and study a heuristic tomographic method that combines variational optimization on tensor networks with randomized measurement techniques. Using this approach, we demonstrate its ability to learn the ground state of the surface code Hamiltonian as well as an experimentally realizable quantum spin liquid state. In particular, we perform numerical experiments using MPS ans\"atze and systematically investigate the sample complexity required to achieve high fidelities for systems of sizes up to $48$ qubits. In addition, we provide theoretical insights into the scaling of our learning algorithm by analyzing the statistical properties of maximum likelihood estimation. Notably, our method is sample-efficient and experimentally friendly, only requiring snapshots of the quantum state measured randomly in the $X$ or $Z$ bases. Using this subset of measurements, our approach can effectively learn any real pure states represented by tensor networks, and we rigorously prove that random-$XZ$ measurements are tomographically complete for such states.

Noise can be helpful for variational quantum algorithms

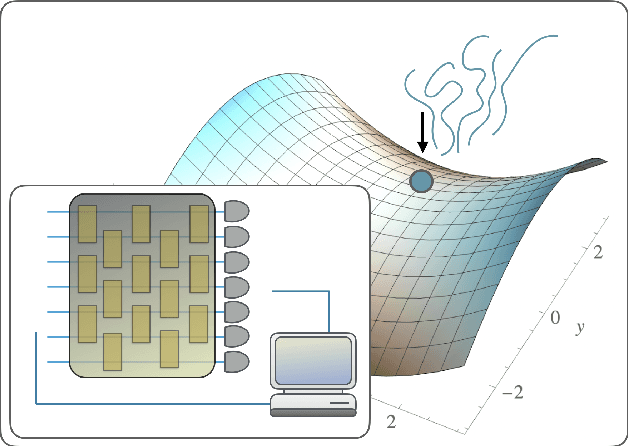
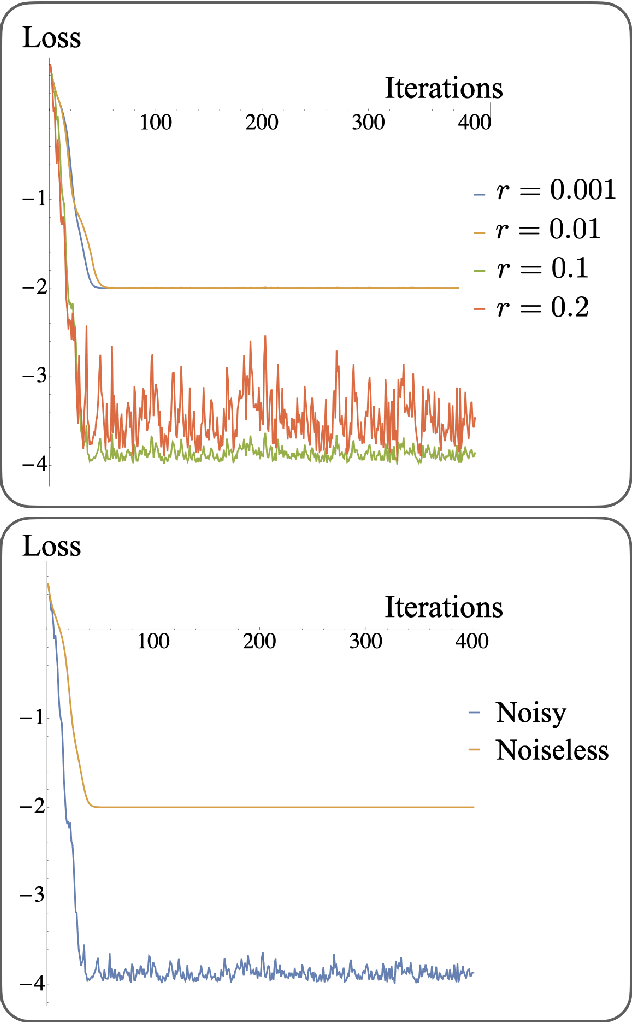
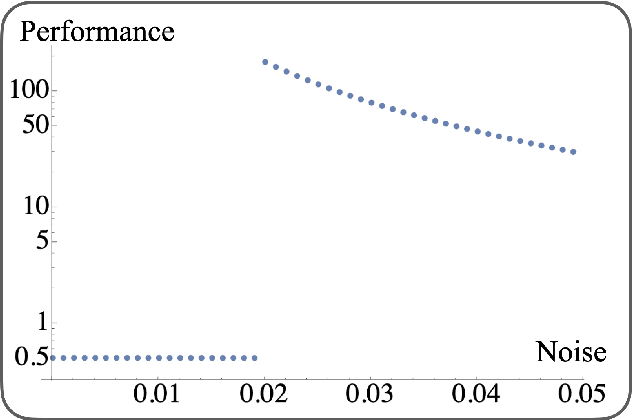
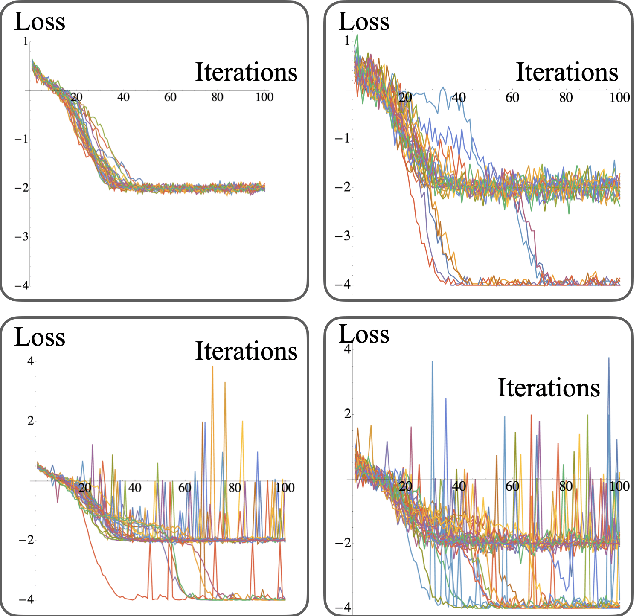
Saddle points constitute a crucial challenge for first-order gradient descent algorithms. In notions of classical machine learning, they are avoided for example by means of stochastic gradient descent methods. In this work, we provide evidence that the saddle points problem can be naturally avoided in variational quantum algorithms by exploiting the presence of stochasticity. We prove convergence guarantees of the approach and its practical functioning at hand of examples. We argue that the natural stochasticity of variational algorithms can be beneficial for avoiding strict saddle points, i.e., those saddle points with at least one negative Hessian eigenvalue. This insight that some noise levels could help in this perspective is expected to add a new perspective to notions of near-term variational quantum algorithms.

Scalably learning quantum many-body Hamiltonians from dynamical data

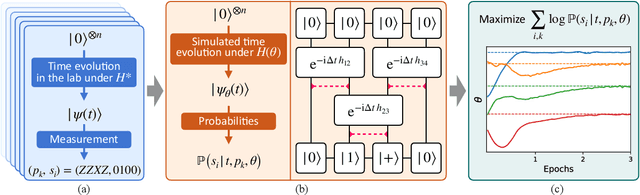
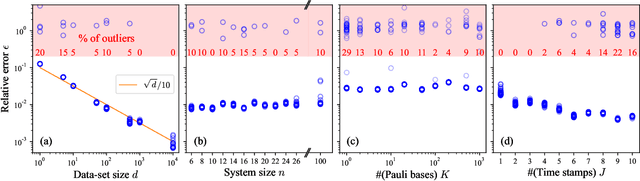
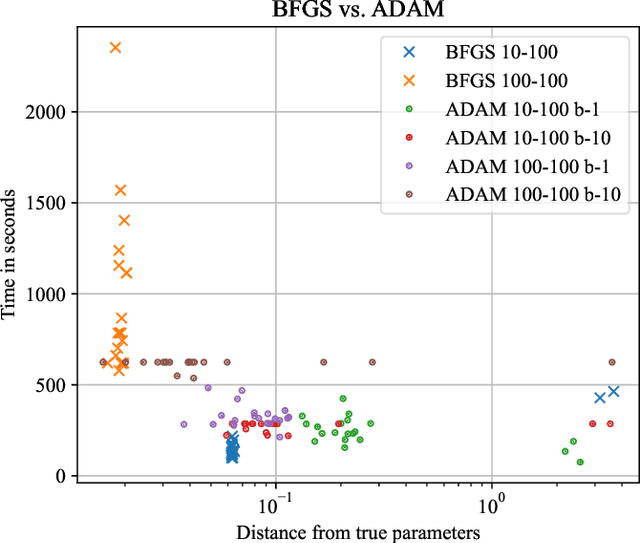
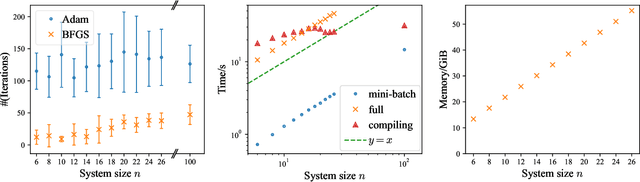
The physics of a closed quantum mechanical system is governed by its Hamiltonian. However, in most practical situations, this Hamiltonian is not precisely known, and ultimately all there is are data obtained from measurements on the system. In this work, we introduce a highly scalable, data-driven approach to learning families of interacting many-body Hamiltonians from dynamical data, by bringing together techniques from gradient-based optimization from machine learning with efficient quantum state representations in terms of tensor networks. Our approach is highly practical, experimentally friendly, and intrinsically scalable to allow for system sizes of above 100 spins. In particular, we demonstrate on synthetic data that the algorithm works even if one is restricted to one simple initial state, a small number of single-qubit observables, and time evolution up to relatively short times. For the concrete example of the one-dimensional Heisenberg model our algorithm exhibits an error constant in the system size and scaling as the inverse square root of the size of the data set.

Single-component gradient rules for variational quantum algorithms

Many near-term quantum computing algorithms are conceived as variational quantum algorithms, in which parameterized quantum circuits are optimized in a hybrid quantum-classical setup. Examples are variational quantum eigensolvers, quantum approximate optimization algorithms as well as various algorithms in the context of quantum-assisted machine learning. A common bottleneck of any such algorithm is constituted by the optimization of the variational parameters. A popular set of optimization methods work on the estimate of the gradient, obtained by means of circuit evaluations. We will refer to the way in which one can combine these circuit evaluations as gradient rules. This work provides a comprehensive picture of the family of gradient rules that vary parameters of quantum gates individually. The most prominent known members of this family are the parameter shift rule and the finite differences method. To unite this family, we propose a generalized parameter shift rule that expresses all members of the aforementioned family as special cases, and discuss how all of these can be seen as providing access to a linear combination of exact first- and second-order derivatives. We further prove that a parameter shift rule with one non-shifted evaluation and only one shifted circuit evaluation can not exist does not exist, and introduce a novel perspective for approaching new gradient rules.

Stochastic gradient descent for hybrid quantum-classical optimization

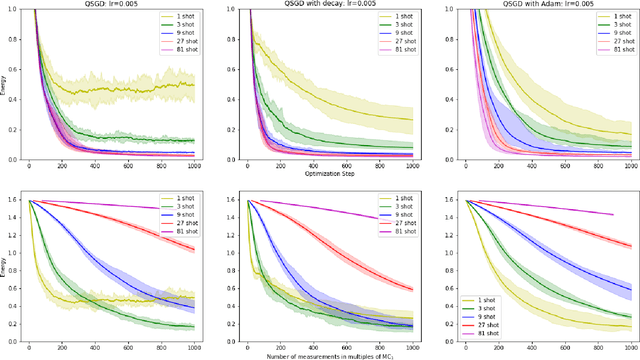
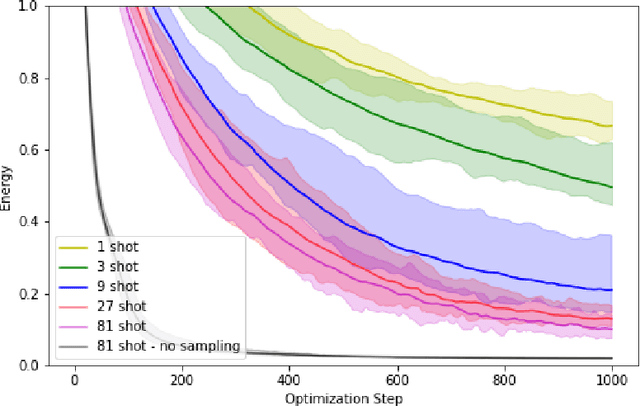
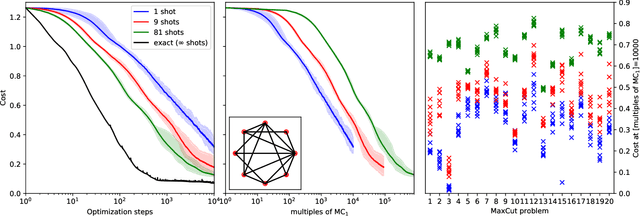
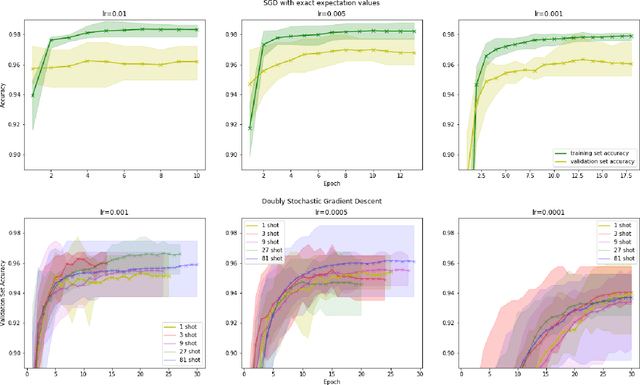
Within the context of hybrid quantum-classical optimization, gradient descent based optimizers typically require the evaluation of expectation values with respect to the outcome of parameterized quantum circuits. In this work, we explore the significant consequences of the simple observation that the estimation of these quantities on quantum hardware is a form of stochastic gradient descent optimization. We formalize this notion, which allows us to show that in many relevant cases, including VQE, QAOA and certain quantum classifiers, estimating expectation values with $k$ measurement outcomes results in optimization algorithms whose convergence properties can be rigorously well understood, for any value of $k$. In fact, even using single measurement outcomes for the estimation of expectation values is sufficient. Moreover, in many settings the required gradients can be expressed as linear combinations of expectation values -- originating, e.g., from a sum over local terms of a Hamiltonian, a parameter shift rule, or a sum over data-set instances -- and we show that in these cases $k$-shot expectation value estimation can be combined with sampling over terms of the linear combination, to obtain "doubly stochastic" gradient descent optimizers. For all algorithms we prove convergence guarantees, providing a framework for the derivation of rigorous optimization results in the context of near-term quantum devices. Additionally, we explore numerically these methods on benchmark VQE, QAOA and quantum-enhanced machine learning tasks and show that treating the stochastic settings as hyper-parameters allows for state-of-the-art results with significantly fewer circuit executions and measurements.