A Bit of Freedom Goes a Long Way: Classical and Quantum Algorithms for Reinforcement Learning under a Generative Model

We propose novel classical and quantum online algorithms for learning finite-horizon and infinite-horizon average-reward Markov Decision Processes (MDPs). Our algorithms are based on a hybrid exploration-generative reinforcement learning (RL) model wherein the agent can, from time to time, freely interact with the environment in a generative sampling fashion, i.e., by having access to a "simulator". By employing known classical and new quantum algorithms for approximating optimal policies under a generative model within our learning algorithms, we show that it is possible to avoid several paradigms from RL like "optimism in the face of uncertainty" and "posterior sampling" and instead compute and use optimal policies directly, which yields better regret bounds compared to previous works. For finite-horizon MDPs, our quantum algorithms obtain regret bounds which only depend logarithmically on the number of time steps $T$, thus breaking the $O(\sqrt{T})$ classical barrier. This matches the time dependence of the prior quantum works of Ganguly et al. (arXiv'23) and Zhong et al. (ICML'24), but with improved dependence on other parameters like state space size $S$ and action space size $A$. For infinite-horizon MDPs, our classical and quantum bounds still maintain the $O(\sqrt{T})$ dependence but with better $S$ and $A$ factors. Nonetheless, we propose a novel measure of regret for infinite-horizon MDPs with respect to which our quantum algorithms have $\operatorname{poly}\log{T}$ regret, exponentially better compared to classical algorithms. Finally, we generalise all of our results to compact state spaces.

Quantum computing and artificial intelligence: status and perspectives

This white paper discusses and explores the various points of intersection between quantum computing and artificial intelligence (AI). It describes how quantum computing could support the development of innovative AI solutions. It also examines use cases of classical AI that can empower research and development in quantum technologies, with a focus on quantum computing and quantum sensing. The purpose of this white paper is to provide a long-term research agenda aimed at addressing foundational questions about how AI and quantum computing interact and benefit one another. It concludes with a set of recommendations and challenges, including how to orchestrate the proposed theoretical work, align quantum AI developments with quantum hardware roadmaps, estimate both classical and quantum resources - especially with the goal of mitigating and optimizing energy consumption - advance this emerging hybrid software engineering discipline, and enhance European industrial competitiveness while considering societal implications.

Probabilistic and Team PFIN-type Learning: General Properties

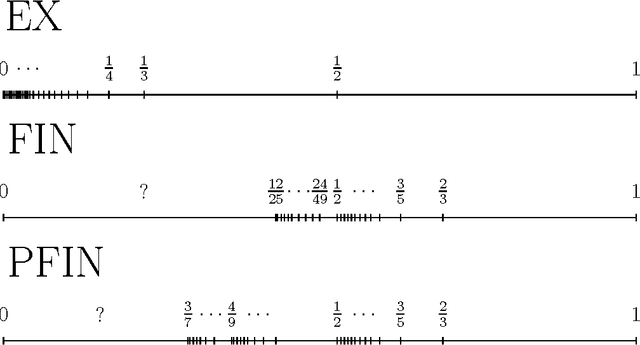
We consider the probability hierarchy for Popperian FINite learning and study the general properties of this hierarchy. We prove that the probability hierarchy is decidable, i.e. there exists an algorithm that receives p_1 and p_2 and answers whether PFIN-type learning with the probability of success p_1 is equivalent to PFIN-type learning with the probability of success p_2. To prove our result, we analyze the topological structure of the probability hierarchy. We prove that it is well-ordered in descending ordering and order-equivalent to ordinal epsilon_0. This shows that the structure of the hierarchy is very complicated. Using similar methods, we also prove that, for PFIN-type learning, team learning and probabilistic learning are of the same power.

Probabilistic Inductive Inference:a Survey

Inductive inference is a recursion-theoretic theory of learning, first developed by E. M. Gold (1967). This paper surveys developments in probabilistic inductive inference. We mainly focus on finite inference of recursive functions, since this simple paradigm has produced the most interesting (and most complex) results.