On Minimax Estimation of Parameters in Softmax-Contaminated Mixture of Experts

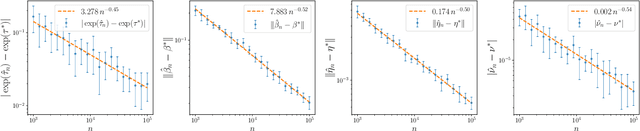
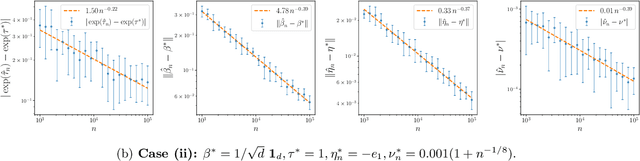
The softmax-contaminated mixture of experts (MoE) model is deployed when a large-scale pre-trained model, which plays the role of a fixed expert, is fine-tuned for learning downstream tasks by including a new contamination part, or prompt, functioning as a new, trainable expert. Despite its popularity and relevance, the theoretical properties of the softmax-contaminated MoE have remained unexplored in the literature. In the paper, we study the convergence rates of the maximum likelihood estimator of gating and prompt parameters in order to gain insights into the statistical properties and potential challenges of fine-tuning with a new prompt. We find that the estimability of these parameters is compromised when the prompt acquires overlapping knowledge with the pre-trained model, in the sense that we make precise by formulating a novel analytic notion of distinguishability. Under distinguishability of the pre-trained and prompt models, we derive minimax optimal estimation rates for all the gating and prompt parameters. By contrast, when the distinguishability condition is violated, these estimation rates become significantly slower due to their dependence on the prompt convergence rate to the pre-trained model. Finally, we empirically corroborate our theoretical findings through several numerical experiments.

Understanding Expert Structures on Minimax Parameter Estimation in Contaminated Mixture of Experts

We conduct the convergence analysis of parameter estimation in the contaminated mixture of experts. This model is motivated from the prompt learning problem where ones utilize prompts, which can be formulated as experts, to fine-tune a large-scaled pre-trained model for learning downstream tasks. There are two fundamental challenges emerging from the analysis: (i) the proportion in the mixture of the pre-trained model and the prompt may converge to zero where the prompt vanishes during the training; (ii) the algebraic interaction among parameters of the pre-trained model and the prompt can occur via some partial differential equation and decelerate the prompt learning. In response, we introduce a distinguishability condition to control the previous parameter interaction. Additionally, we also consider various types of expert structures to understand their effects on the parameter estimation. In each scenario, we provide comprehensive convergence rates of parameter estimation along with the corresponding minimax lower bounds.

Statistical Perspective of Top-K Sparse Softmax Gating Mixture of Experts

Top-K sparse softmax gating mixture of experts has been widely used for scaling up massive deep-learning architectures without increasing the computational cost. Despite its popularity in real-world applications, the theoretical understanding of that gating function has remained an open problem. The main challenge comes from the structure of the top-K sparse softmax gating function, which partitions the input space into multiple regions with distinct behaviors. By focusing on a Gaussian mixture of experts, we establish theoretical results on the effects of the top-K sparse softmax gating function on both density and parameter estimations. Our results hinge upon defining novel loss functions among parameters to capture different behaviors of the input regions. When the true number of experts $k_{\ast}$ is known, we demonstrate that the convergence rates of density and parameter estimations are both parametric on the sample size. However, when $k_{\ast}$ becomes unknown and the true model is over-specified by a Gaussian mixture of $k$ experts where $k > k_{\ast}$, our findings suggest that the number of experts selected from the top-K sparse softmax gating function must exceed the total cardinality of a certain number of Voronoi cells associated with the true parameters to guarantee the convergence of the density estimation. Moreover, while the density estimation rate remains parametric under this setting, the parameter estimation rates become substantially slow due to an intrinsic interaction between the softmax gating and expert functions.

Scaling up Hybrid Probabilistic Inference with Logical and Arithmetic Constraints via Message Passing

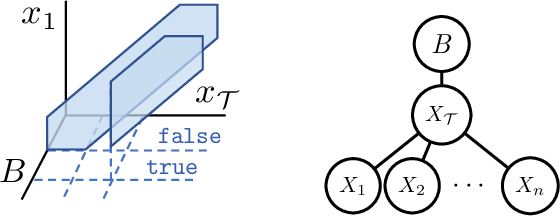
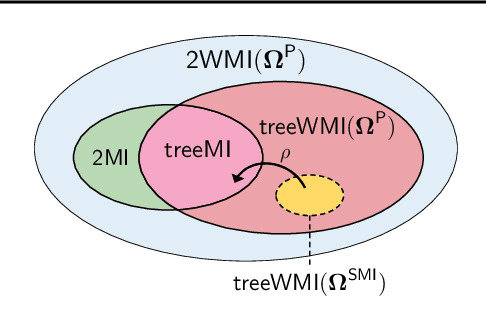
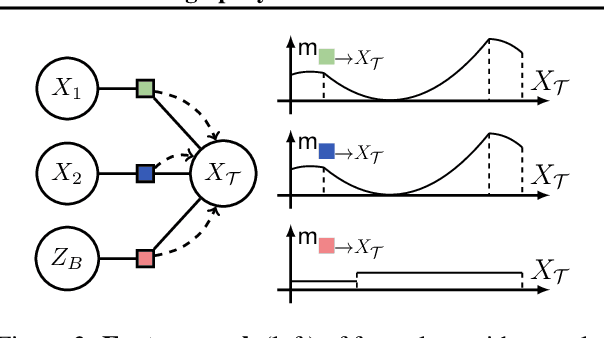
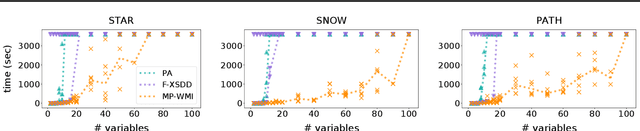
Weighted model integration (WMI) is a very appealing framework for probabilistic inference: it allows to express the complex dependencies of real-world problems where variables are both continuous and discrete, via the language of Satisfiability Modulo Theories (SMT), as well as to compute probabilistic queries with complex logical and arithmetic constraints. Yet, existing WMI solvers are not ready to scale to these problems. They either ignore the intrinsic dependency structure of the problem at all, or they are limited to too restrictive structures. To narrow this gap, we derive a factorized formalism of WMI enabling us to devise a scalable WMI solver based on message passing, MP-WMI. Namely, MP-WMI is the first WMI solver which allows to: 1) perform exact inference on the full class of tree-structured WMI problems; 2) compute all marginal densities in linear time; 3) amortize inference inter query. Experimental results show that our solver dramatically outperforms the existing WMI solvers on a large set of benchmarks.

Hybrid Probabilistic Inference with Logical Constraints: Tractability and Message Passing

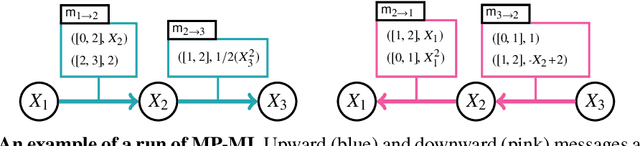
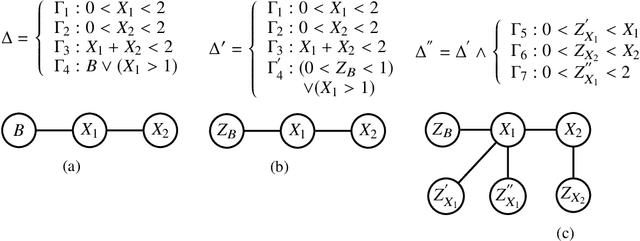
Weighted model integration (WMI) is a very appealing framework for probabilistic inference: it allows to express the complex dependencies of real-world hybrid scenarios where variables are heterogeneous in nature (both continuous and discrete) via the language of Satisfiability Modulo Theories (SMT); as well as computing probabilistic queries with arbitrarily complex logical constraints. Recent work has shown WMI inference to be reducible to a model integration (MI) problem, under some assumptions, thus effectively allowing hybrid probabilistic reasoning by volume computations. In this paper, we introduce a novel formulation of MI via a message passing scheme that allows to efficiently compute the marginal densities and statistical moments of all the variables in linear time. As such, we are able to amortize inference for arbitrarily rich MI queries when they conform to the problem structure, here represented as the primal graph associated to the SMT formula. Furthermore, we theoretically trace the tractability boundaries of exact MI. Indeed, we prove that in terms of the structural requirements on the primal graph that make our MI algorithm tractable - bounding its diameter and treewidth - the bounds are not only sufficient, but necessary for tractable inference via MI.