On Minimax Estimation of Parameters in Softmax-Contaminated Mixture of Experts

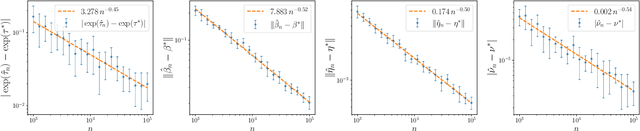
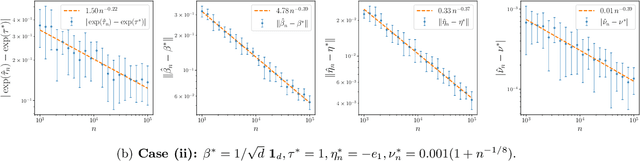
The softmax-contaminated mixture of experts (MoE) model is deployed when a large-scale pre-trained model, which plays the role of a fixed expert, is fine-tuned for learning downstream tasks by including a new contamination part, or prompt, functioning as a new, trainable expert. Despite its popularity and relevance, the theoretical properties of the softmax-contaminated MoE have remained unexplored in the literature. In the paper, we study the convergence rates of the maximum likelihood estimator of gating and prompt parameters in order to gain insights into the statistical properties and potential challenges of fine-tuning with a new prompt. We find that the estimability of these parameters is compromised when the prompt acquires overlapping knowledge with the pre-trained model, in the sense that we make precise by formulating a novel analytic notion of distinguishability. Under distinguishability of the pre-trained and prompt models, we derive minimax optimal estimation rates for all the gating and prompt parameters. By contrast, when the distinguishability condition is violated, these estimation rates become significantly slower due to their dependence on the prompt convergence rate to the pre-trained model. Finally, we empirically corroborate our theoretical findings through several numerical experiments.

On DeepSeekMoE: Statistical Benefits of Shared Experts and Normalized Sigmoid Gating

Mixture of experts (MoE) methods are a key component in most large language model architectures, including the recent series of DeepSeek models. Compared to other MoE implementations, DeepSeekMoE stands out because of two unique features: the deployment of a shared expert strategy and of the normalized sigmoid gating mechanism. Despite the prominent role of DeepSeekMoE in the success of the DeepSeek series of models, there have been only a few attempts to justify theoretically the value of the shared expert strategy, while its normalized sigmoid gating has remained unexplored. To bridge this gap, we undertake a comprehensive theoretical study of these two features of DeepSeekMoE from a statistical perspective. We perform a convergence analysis of the expert estimation task to highlight the gains in sample efficiency for both the shared expert strategy and the normalized sigmoid gating, offering useful insights into the design of expert and gating structures. To verify empirically our theoretical findings, we carry out several experiments on both synthetic data and real-world datasets for (vision) language modeling tasks. Finally, we conduct an extensive empirical analysis of the router behaviors, ranging from router saturation, router change rate, to expert utilization.

Convergence Rates for Softmax Gating Mixture of Experts

Mixture of experts (MoE) has recently emerged as an effective framework to advance the efficiency and scalability of machine learning models by softly dividing complex tasks among multiple specialized sub-models termed experts. Central to the success of MoE is an adaptive softmax gating mechanism which takes responsibility for determining the relevance of each expert to a given input and then dynamically assigning experts their respective weights. Despite its widespread use in practice, a comprehensive study on the effects of the softmax gating on the MoE has been lacking in the literature. To bridge this gap in this paper, we perform a convergence analysis of parameter estimation and expert estimation under the MoE equipped with the standard softmax gating or its variants, including a dense-to-sparse gating and a hierarchical softmax gating, respectively. Furthermore, our theories also provide useful insights into the design of sample-efficient expert structures. In particular, we demonstrate that it requires polynomially many data points to estimate experts satisfying our proposed \emph{strong identifiability} condition, namely a commonly used two-layer feed-forward network. In stark contrast, estimating linear experts, which violate the strong identifiability condition, necessitates exponentially many data points as a result of intrinsic parameter interactions expressed in the language of partial differential equations. All the theoretical results are substantiated with a rigorous guarantee.

Uncertainty quantification for Markov chains with application to temporal difference learning

Markov chains are fundamental to statistical machine learning, underpinning key methodologies such as Markov Chain Monte Carlo (MCMC) sampling and temporal difference (TD) learning in reinforcement learning (RL). Given their widespread use, it is crucial to establish rigorous probabilistic guarantees on their convergence, uncertainty, and stability. In this work, we develop novel, high-dimensional concentration inequalities and Berry-Esseen bounds for vector- and matrix-valued functions of Markov chains, addressing key limitations in existing theoretical tools for handling dependent data. We leverage these results to analyze the TD learning algorithm, a widely used method for policy evaluation in RL. Our analysis yields a sharp high-probability consistency guarantee that matches the asymptotic variance up to logarithmic factors. Furthermore, we establish a $O(T^{-\frac{1}{4}}\log T)$ distributional convergence rate for the Gaussian approximation of the TD estimator, measured in convex distance. These findings provide new insights into statistical inference for RL algorithms, bridging the gaps between classical stochastic approximation theory and modern reinforcement learning applications.

Statistical Inference for Temporal Difference Learning with Linear Function Approximation

Statistical inference with finite-sample validity for the value function of a given policy in Markov decision processes (MDPs) is crucial for ensuring the reliability of reinforcement learning. Temporal Difference (TD) learning, arguably the most widely used algorithm for policy evaluation, serves as a natural framework for this purpose.In this paper, we study the consistency properties of TD learning with Polyak-Ruppert averaging and linear function approximation, and obtain three significant improvements over existing results. First, we derive a novel sharp high-dimensional probability convergence guarantee that depends explicitly on the asymptotic variance and holds under weak conditions. We further establish refined high-dimensional Berry-Esseen bounds over the class of convex sets that guarantee faster rates than those in the literature. Finally, we propose a plug-in estimator for the asymptotic covariance matrix, designed for efficient online computation. These results enable the construction of confidence regions and simultaneous confidence intervals for the linear parameters of the value function, with guaranteed finite-sample coverage. We demonstrate the applicability of our theoretical findings through numerical experiments.

Straightness of Rectified Flow: A Theoretical Insight into Wasserstein Convergence

Diffusion models have emerged as a powerful tool for image generation and denoising. Typically, generative models learn a trajectory between the starting noise distribution and the target data distribution. Recently Liu et al. (2023b) designed a novel alternative generative model Rectified Flow (RF), which aims to learn straight flow trajectories from noise to data using a sequence of convex optimization problems with close ties to optimal transport. If the trajectory is curved, one must use many Euler discretization steps or novel strategies, such as exponential integrators, to achieve a satisfactory generation quality. In contrast, RF has been shown to theoretically straighten the trajectory through successive rectifications, reducing the number of function evaluations (NFEs) while sampling. It has also been shown empirically that RF may improve the straightness in two rectifications if one can solve the underlying optimization problem within a sufficiently small error. In this paper, we make two key theoretical contributions: 1) we provide the first theoretical analysis of the Wasserstein distance between the sampling distribution of RF and the target distribution. Our error rate is characterized by the number of discretization steps and a new formulation of straightness stronger than that in the original work. 2) In line with the previous empirical findings, we show that, for a rectified flow from a Gaussian to a mixture of two Gaussians, two rectifications are sufficient to achieve a straight flow. Additionally, we also present empirical results on both simulated and real datasets to validate our theoretical findings.

Sigmoid Gating is More Sample Efficient than Softmax Gating in Mixture of Experts

The softmax gating function is arguably the most popular choice in mixture of experts modeling. Despite its widespread use in practice, softmax gating may lead to unnecessary competition among experts, potentially causing the undesirable phenomenon of representation collapse due to its inherent structure. In response, the sigmoid gating function has been recently proposed as an alternative and has been demonstrated empirically to achieve superior performance. However, a rigorous examination of the sigmoid gating function is lacking in current literature. In this paper, we verify theoretically that sigmoid gating, in fact, enjoys a higher sample efficiency than softmax gating for the statistical task of expert estimation. Towards that goal, we consider a regression framework in which the unknown regression function is modeled as a mixture of experts, and study the rates of convergence of the least squares estimator in the over-specified case in which the number of experts fitted is larger than the true value. We show that two gating regimes naturally arise and, in each of them, we formulate identifiability conditions for the expert functions and derive the corresponding convergence rates. In both cases, we find that experts formulated as feed-forward networks with commonly used activation such as $\mathrm{ReLU}$ and $\mathrm{GELU}$ enjoy faster convergence rates under sigmoid gating than softmax gating. Furthermore, given the same choice of experts, we demonstrate that the sigmoid gating function requires a smaller sample size than its softmax counterpart to attain the same error of expert estimation and, therefore, is more sample efficient.

On Least Squares Estimation in Softmax Gating Mixture of Experts

Mixture of experts (MoE) model is a statistical machine learning design that aggregates multiple expert networks using a softmax gating function in order to form a more intricate and expressive model. Despite being commonly used in several applications owing to their scalability, the mathematical and statistical properties of MoE models are complex and difficult to analyze. As a result, previous theoretical works have primarily focused on probabilistic MoE models by imposing the impractical assumption that the data are generated from a Gaussian MoE model. In this work, we investigate the performance of the least squares estimators (LSE) under a deterministic MoE model where the data are sampled according to a regression model, a setting that has remained largely unexplored. We establish a condition called strong identifiability to characterize the convergence behavior of various types of expert functions. We demonstrate that the rates for estimating strongly identifiable experts, namely the widely used feed forward networks with activation functions $\mathrm{sigmoid}(\cdot)$ and $\tanh(\cdot)$, are substantially faster than those of polynomial experts, which we show to exhibit a surprising slow estimation rate. Our findings have important practical implications for expert selection.

Sharp high-probability sample complexities for policy evaluation with linear function approximation

This paper is concerned with the problem of policy evaluation with linear function approximation in discounted infinite horizon Markov decision processes. We investigate the sample complexities required to guarantee a predefined estimation error of the best linear coefficients for two widely-used policy evaluation algorithms: the temporal difference (TD) learning algorithm and the two-timescale linear TD with gradient correction (TDC) algorithm. In both the on-policy setting, where observations are generated from the target policy, and the off-policy setting, where samples are drawn from a behavior policy potentially different from the target policy, we establish the first sample complexity bound with high-probability convergence guarantee that attains the optimal dependence on the tolerance level. We also exhihit an explicit dependence on problem-related quantities, and show in the on-policy setting that our upper bound matches the minimax lower bound on crucial problem parameters, including the choice of the feature maps and the problem dimension.

Mitigating multiple descents: A model-agnostic framework for risk monotonization

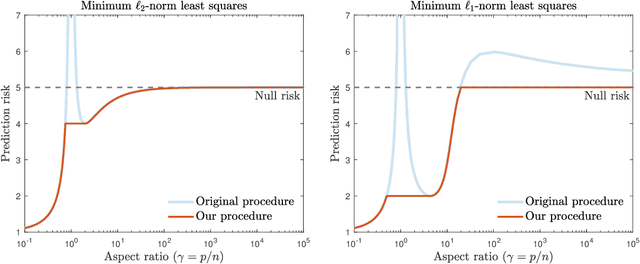
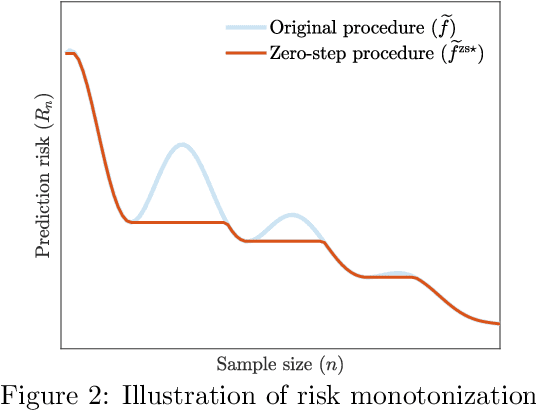
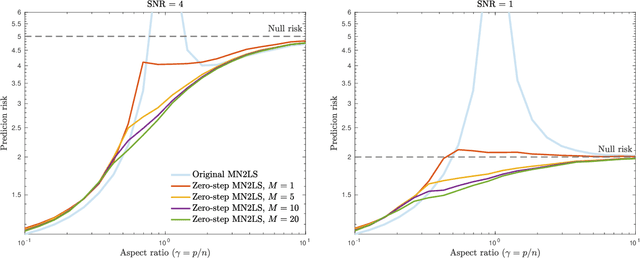
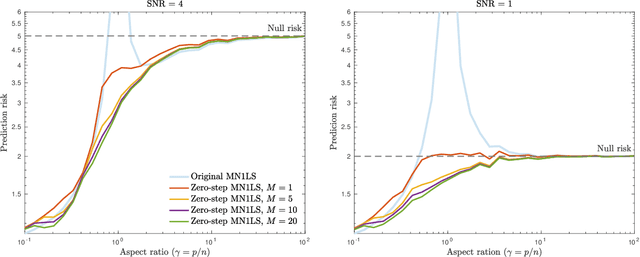
Recent empirical and theoretical analyses of several commonly used prediction procedures reveal a peculiar risk behavior in high dimensions, referred to as double/multiple descent, in which the asymptotic risk is a non-monotonic function of the limiting aspect ratio of the number of features or parameters to the sample size. To mitigate this undesirable behavior, we develop a general framework for risk monotonization based on cross-validation that takes as input a generic prediction procedure and returns a modified procedure whose out-of-sample prediction risk is, asymptotically, monotonic in the limiting aspect ratio. As part of our framework, we propose two data-driven methodologies, namely zero- and one-step, that are akin to bagging and boosting, respectively, and show that, under very mild assumptions, they provably achieve monotonic asymptotic risk behavior. Our results are applicable to a broad variety of prediction procedures and loss functions, and do not require a well-specified (parametric) model. We exemplify our framework with concrete analyses of the minimum $\ell_2$, $\ell_1$-norm least squares prediction procedures. As one of the ingredients in our analysis, we also derive novel additive and multiplicative forms of oracle risk inequalities for split cross-validation that are of independent interest.