A Quantum-Driven Evolutionary Framework for Solving High-Dimensional Sharpe Ratio Portfolio Optimization

High-dimensional portfolio optimization faces significant computational challenges under complex constraints, with traditional optimization methods struggling to balance convergence speed and global exploration capability. To address this, firstly, we introduce an enhanced Sharpe ratio-based model that incorporates all constraints into the objective function using adaptive penalty terms, transforming the original constrained problem into an unconstrained single-objective formulation. This approach preserves financial interpretability while simplifying algorithmic implementation. To efficiently solve the resulting high-dimensional optimization problem, we propose a Quantum Hybrid Differential Evolution (QHDE) algorithm, which integrates Quantum-inspired probabilistic behavior into the standard DE framework. QHDE employs a Schrodinger-inspired probabilistic mechanism for population evolution, enabling more flexible and diversified solution updates. To further enhance performance, a good point set-chaos reverse learning strategy is adopted to generate a well-dispersed initial population, and a dynamic elite pool combined with Cauchy-Gaussian hybrid perturbations strengthens global exploration and mitigates premature convergence. Experimental validation on CEC benchmarks and real-world portfolios involving 20 to 80 assets demonstrates that QHDE's performance improves by up to 73.4%. It attains faster convergence, higher solution precision, and greater robustness than seven state-of-the-art counterparts, thereby confirming its suitability for complex, high-dimensional portfolio optimization and advancing quantum-inspired evolutionary research in computational finance.

OPAL: Operator-Programmed Algorithms for Landscape-Aware Black-Box Optimization

Black-box optimization often relies on evolutionary and swarm algorithms whose performance is highly problem dependent. We view an optimizer as a short program over a small vocabulary of search operators and learn this operator program separately for each problem instance. We instantiate this idea in Operator-Programmed Algorithms (OPAL), a landscape-aware framework for continuous black-box optimization that uses a small design budget with a standard differential evolution baseline to probe the landscape, builds a $k$-nearest neighbor graph over sampled points, and encodes this trajectory with a graph neural network. A meta-learner then maps the resulting representation to a phase-wise schedule of exploration, restart, and local search operators. On the CEC~2017 test suite, a single meta-trained OPAL policy is statistically competitive with state-of-the-art adaptive differential evolution variants and achieves significant improvements over simpler baselines under nonparametric tests. Ablation studies on CEC~2017 justify the choices for the design phase, the trajectory graph, and the operator-program representation, while the meta-components add only modest wall-clock overhead. Overall, the results indicate that operator-programmed, landscape-aware per-instance design is a practical way forward beyond ad hoc metaphor-based algorithms in black-box optimization.

Deep Learning for Lung Cancer Detection: Tackling the Kaggle Data Science Bowl 2017 Challenge

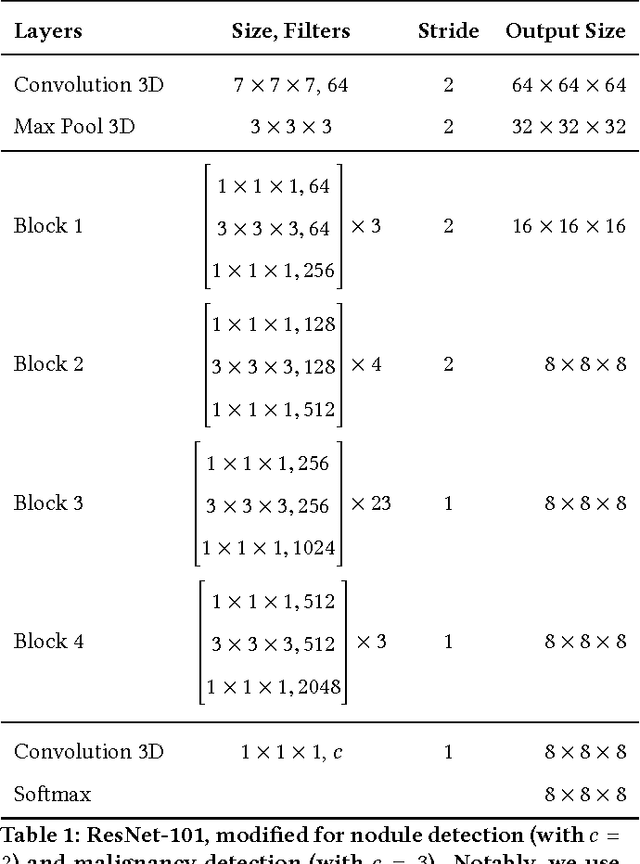
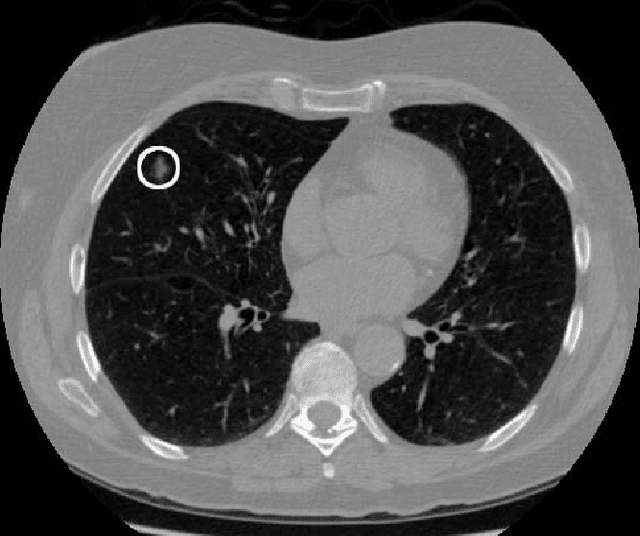
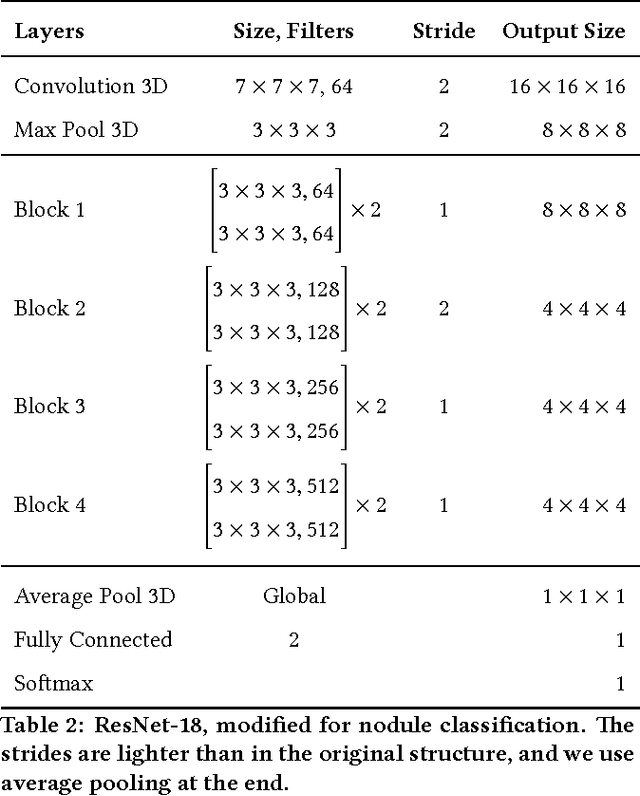
We present a deep learning framework for computer-aided lung cancer diagnosis. Our multi-stage framework detects nodules in 3D lung CAT scans, determines if each nodule is malignant, and finally assigns a cancer probability based on these results. We discuss the challenges and advantages of our framework. In the Kaggle Data Science Bowl 2017, our framework ranked 41st out of 1972 teams.