A Quantum-Driven Evolutionary Framework for Solving High-Dimensional Sharpe Ratio Portfolio Optimization

High-dimensional portfolio optimization faces significant computational challenges under complex constraints, with traditional optimization methods struggling to balance convergence speed and global exploration capability. To address this, firstly, we introduce an enhanced Sharpe ratio-based model that incorporates all constraints into the objective function using adaptive penalty terms, transforming the original constrained problem into an unconstrained single-objective formulation. This approach preserves financial interpretability while simplifying algorithmic implementation. To efficiently solve the resulting high-dimensional optimization problem, we propose a Quantum Hybrid Differential Evolution (QHDE) algorithm, which integrates Quantum-inspired probabilistic behavior into the standard DE framework. QHDE employs a Schrodinger-inspired probabilistic mechanism for population evolution, enabling more flexible and diversified solution updates. To further enhance performance, a good point set-chaos reverse learning strategy is adopted to generate a well-dispersed initial population, and a dynamic elite pool combined with Cauchy-Gaussian hybrid perturbations strengthens global exploration and mitigates premature convergence. Experimental validation on CEC benchmarks and real-world portfolios involving 20 to 80 assets demonstrates that QHDE's performance improves by up to 73.4%. It attains faster convergence, higher solution precision, and greater robustness than seven state-of-the-art counterparts, thereby confirming its suitability for complex, high-dimensional portfolio optimization and advancing quantum-inspired evolutionary research in computational finance.

A Novel Sleep Stage Classification Using CNN Generated by an Efficient Neural Architecture Search with a New Data Processing Trick

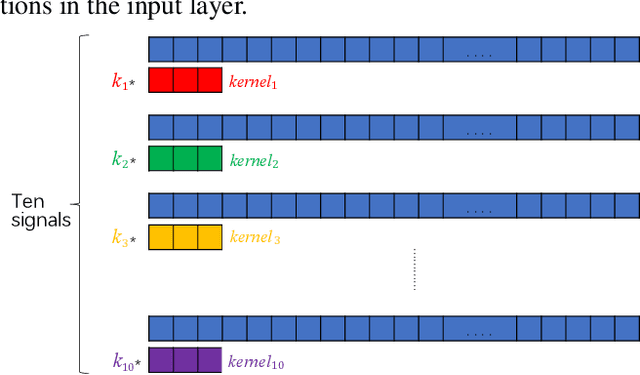
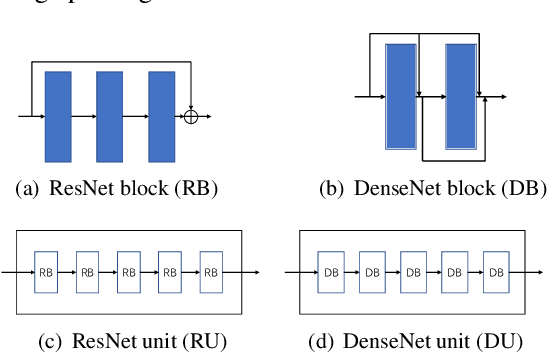
With the development of automatic sleep stage classification (ASSC) techniques, many classical methods such as k-means, decision tree, and SVM have been used in automatic sleep stage classification. However, few methods explore deep learning on ASSC. Meanwhile, most deep learning methods require extensive expertise and suffer from a mass of handcrafted steps which are time-consuming especially when dealing with multi-classification tasks. In this paper, we propose an efficient five-sleep-stage classification method using convolutional neural networks (CNNs) with a novel data processing trick and we design neural architecture search (NAS) technique based on genetic algorithm (GA), NAS-G, to search for the best CNN architecture. Firstly, we attach each kernel with an adaptive coefficient to enhance the signal processing of the inputs. This can enhance the propagation of informative features and suppress the propagation of useless features in the early stage of the network. Then, we make full use of GA's heuristic search and the advantage of no need for the gradient to search for the best architecture of CNN. This can achieve a CNN with better performance than a handcrafted one in a large search space at the minimum cost. We verify the convergence of our data processing trick and compare the performance of traditional CNNs before and after using our trick. Meanwhile, we compare the performance between the CNN generated through NAS-G and the traditional CNNs with our trick. The experiments demonstrate that the convergence of CNNs with data processing trick is faster than without data processing trick and the CNN with data processing trick generated by NAS-G outperforms the handcrafted counterparts that use the data processing trick too.

Monkey Optimization System with Active Membranes: A New Meta-heuristic Optimization System

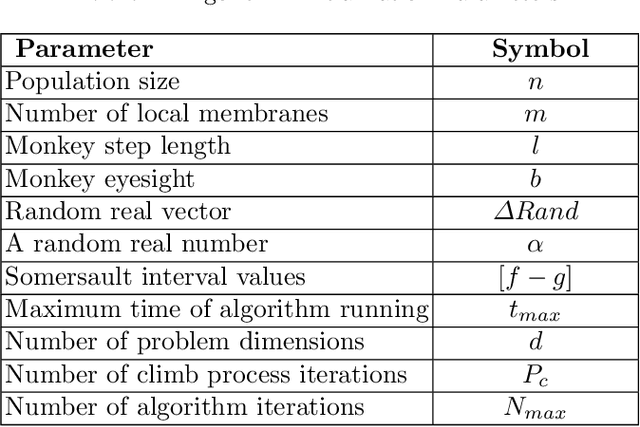
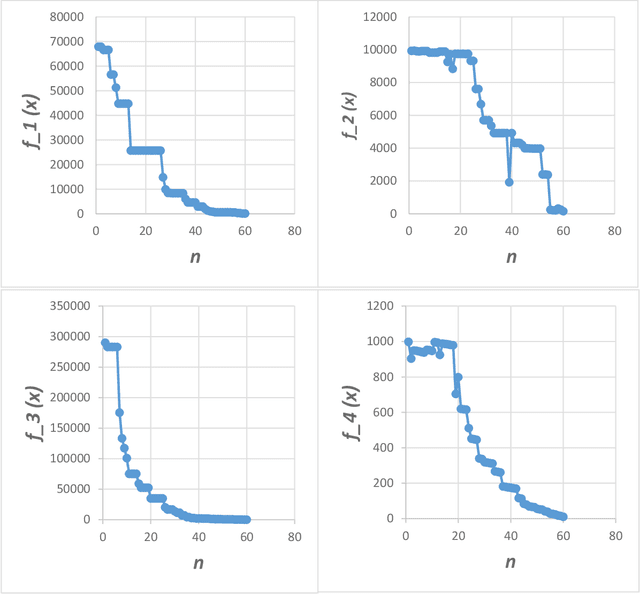
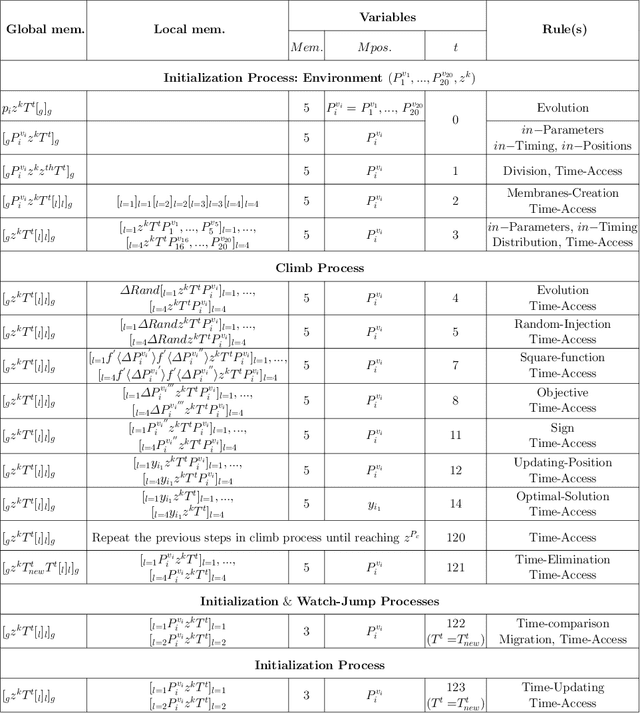
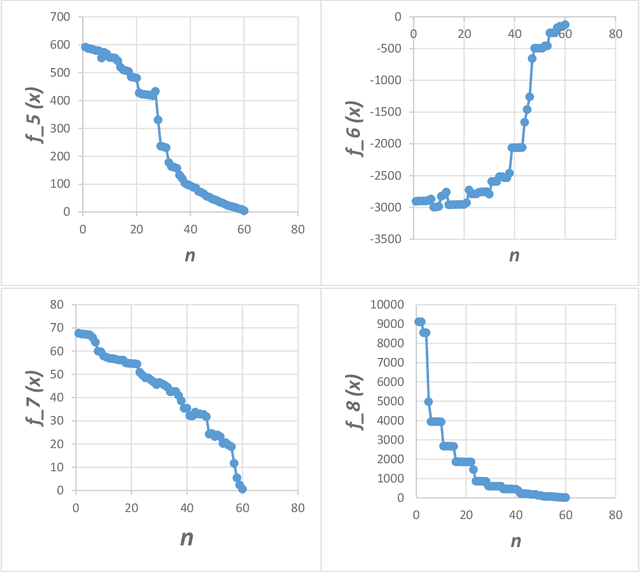
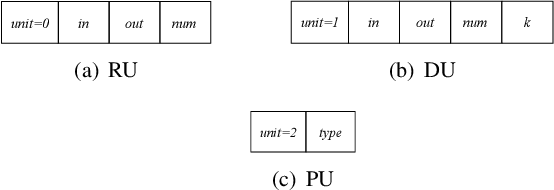
Optimization techniques, used to get the optimal solution in search spaces, have not solved the time-consuming problem. The objective of this study is to tackle the sequential processing problem in Monkey Algorithm and simulating the natural parallel behavior of monkeys. Therefore, a P system with active membranes is constructed by providing a codification for Monkey Algorithm within the context of a cell-like P system, defining accordingly the elements of the model - membrane structure, objects, rules and the behavior of it. The proposed algorithm has modeled the natural behavior of climb process using separate membranes, rather than the original algorithm. Moreover, it introduced the membrane migration process to select the best solution and the time stamp was added as an additional stopping criterion to control the timing of the algorithm. The results indicate a substantial solution for the time consumption problem, significant representation of the natural behavior of monkeys, and considerable chance to reach the best solution in the context of meta-heuristics purpose. In addition, experiments use the commonly used benchmark functions to test the performance of the algorithm as well as the expected time of the proposed P Monkey optimization algorithm and the traditional Monkey Algorithm running on population size. The unit times are calculated based on the complexity of algorithms, where P Monkey takes a time unit to fire rule(s) over a population size n; as soon as, Monkey Algorithm takes a time unit to run a step every mathematical equation over a population size.