Hsin-Yuan Huang
Quantum advantage in learning from experiments
Dec 01, 2021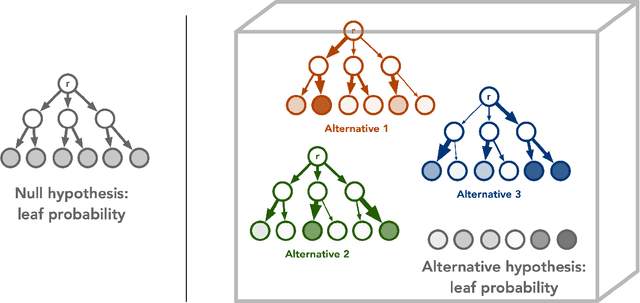

Abstract:Quantum technology has the potential to revolutionize how we acquire and process experimental data to learn about the physical world. An experimental setup that transduces data from a physical system to a stable quantum memory, and processes that data using a quantum computer, could have significant advantages over conventional experiments in which the physical system is measured and the outcomes are processed using a classical computer. We prove that, in various tasks, quantum machines can learn from exponentially fewer experiments than those required in conventional experiments. The exponential advantage holds in predicting properties of physical systems, performing quantum principal component analysis on noisy states, and learning approximate models of physical dynamics. In some tasks, the quantum processing needed to achieve the exponential advantage can be modest; for example, one can simultaneously learn about many noncommuting observables by processing only two copies of the system. Conducting experiments with up to 40 superconducting qubits and 1300 quantum gates, we demonstrate that a substantial quantum advantage can be realized using today's relatively noisy quantum processors. Our results highlight how quantum technology can enable powerful new strategies to learn about nature.
Exponential separations between learning with and without quantum memory
Nov 18, 2021
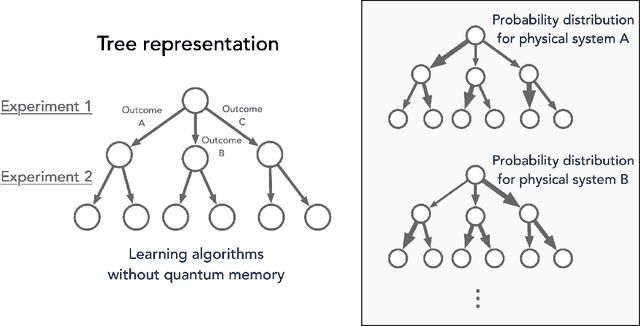
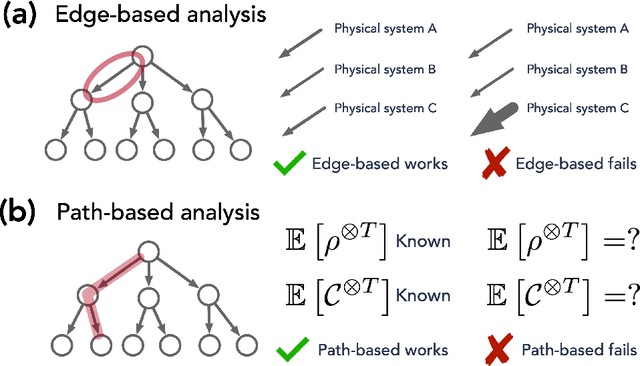
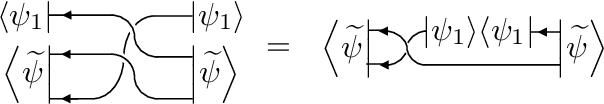
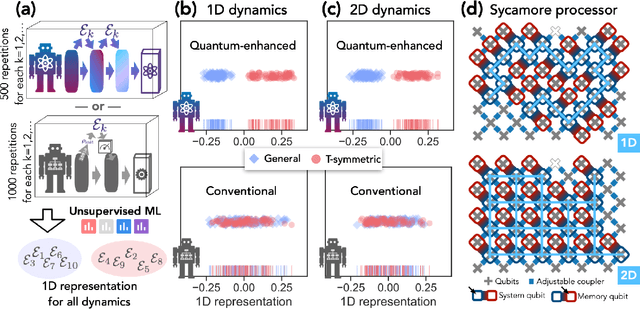
Abstract:We study the power of quantum memory for learning properties of quantum systems and dynamics, which is of great importance in physics and chemistry. Many state-of-the-art learning algorithms require access to an additional external quantum memory. While such a quantum memory is not required a priori, in many cases, algorithms that do not utilize quantum memory require much more data than those which do. We show that this trade-off is inherent in a wide range of learning problems. Our results include the following: (1) We show that to perform shadow tomography on an $n$-qubit state rho with $M$ observables, any algorithm without quantum memory requires $\Omega(\min(M, 2^n))$ samples of rho in the worst case. Up to logarithmic factors, this matches the upper bound of [HKP20] and completely resolves an open question in [Aar18, AR19]. (2) We establish exponential separations between algorithms with and without quantum memory for purity testing, distinguishing scrambling and depolarizing evolutions, as well as uncovering symmetry in physical dynamics. Our separations improve and generalize prior work of [ACQ21] by allowing for a broader class of algorithms without quantum memory. (3) We give the first tradeoff between quantum memory and sample complexity. We prove that to estimate absolute values of all $n$-qubit Pauli observables, algorithms with $k < n$ qubits of quantum memory require at least $\Omega(2^{(n-k)/3})$ samples, but there is an algorithm using $n$-qubit quantum memory which only requires $O(n)$ samples. The separations we show are sufficiently large and could already be evident, for instance, with tens of qubits. This provides a concrete path towards demonstrating real-world advantage for learning algorithms with quantum memory.
A Hierarchy for Replica Quantum Advantage
Nov 10, 2021
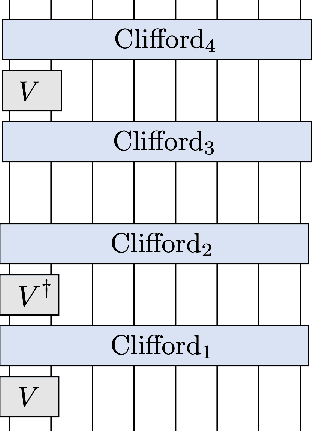
Abstract:We prove that given the ability to make entangled measurements on at most $k$ replicas of an $n$-qubit state $\rho$ simultaneously, there is a property of $\rho$ which requires at least order $2^n / k^2$ measurements to learn. However, the same property only requires one measurement to learn if we can make an entangled measurement over a number of replicas polynomial in $k, n$. Because the above holds for each positive integer $k$, we obtain a hierarchy of tasks necessitating progressively more replicas to be performed efficiently. We introduce a powerful proof technique to establish our results, and also use this to provide new bounds for testing the mixedness of a quantum state.
Generalization in quantum machine learning from few training data
Nov 09, 2021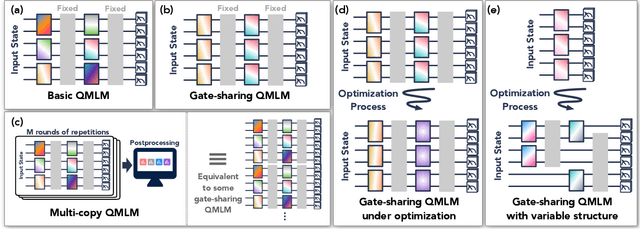
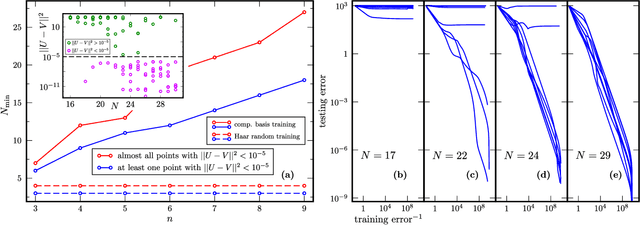
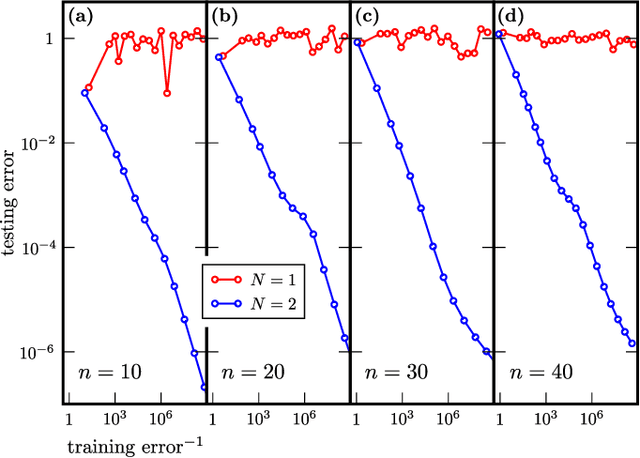
Abstract:Modern quantum machine learning (QML) methods involve variationally optimizing a parameterized quantum circuit on a training data set, and subsequently making predictions on a testing data set (i.e., generalizing). In this work, we provide a comprehensive study of generalization performance in QML after training on a limited number $N$ of training data points. We show that the generalization error of a quantum machine learning model with $T$ trainable gates scales at worst as $\sqrt{T/N}$. When only $K \ll T$ gates have undergone substantial change in the optimization process, we prove that the generalization error improves to $\sqrt{K / N}$. Our results imply that the compiling of unitaries into a polynomial number of native gates, a crucial application for the quantum computing industry that typically uses exponential-size training data, can be sped up significantly. We also show that classification of quantum states across a phase transition with a quantum convolutional neural network requires only a very small training data set. Other potential applications include learning quantum error correcting codes or quantum dynamical simulation. Our work injects new hope into the field of QML, as good generalization is guaranteed from few training data.
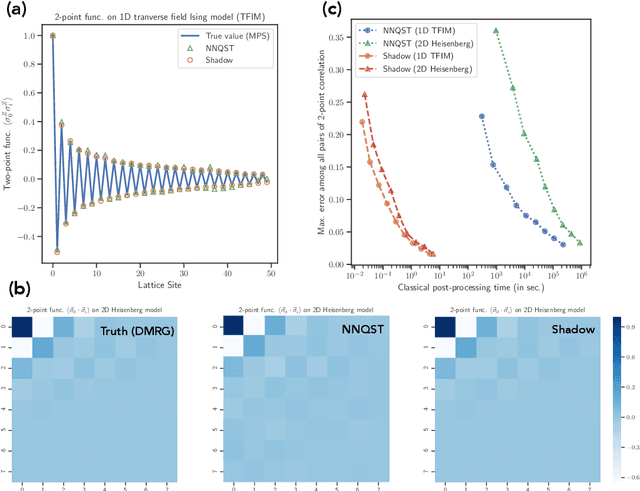
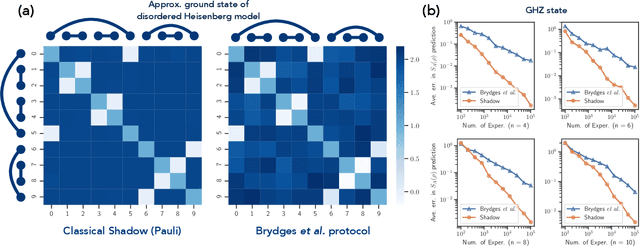
Provably efficient machine learning for quantum many-body problems
Jul 18, 2021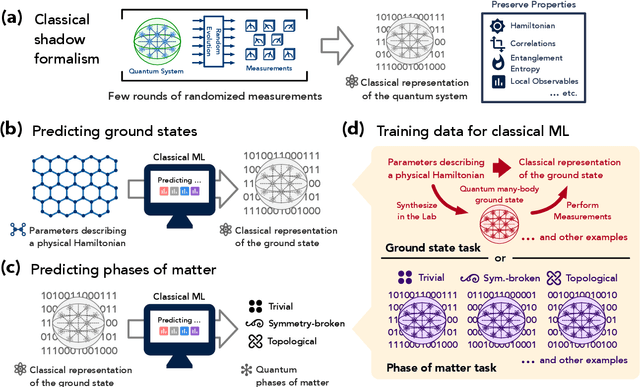
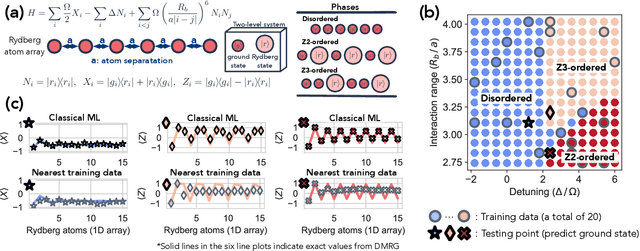
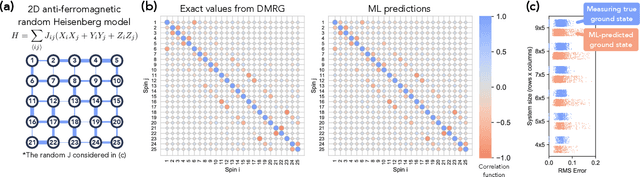
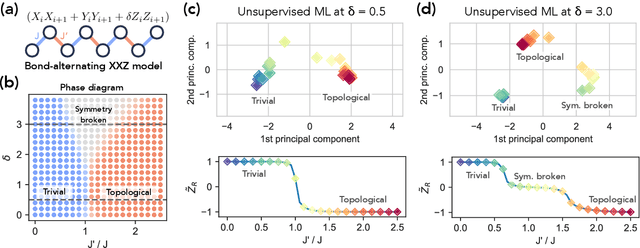
Abstract:Classical machine learning (ML) provides a potentially powerful approach to solving challenging quantum many-body problems in physics and chemistry. However, the advantages of ML over more traditional methods have not been firmly established. In this work, we prove that classical ML algorithms can efficiently predict ground state properties of gapped Hamiltonians in finite spatial dimensions, after learning from data obtained by measuring other Hamiltonians in the same quantum phase of matter. In contrast, under widely accepted complexity theory assumptions, classical algorithms that do not learn from data cannot achieve the same guarantee. We also prove that classical ML algorithms can efficiently classify a wide range of quantum phases of matter. Our arguments are based on the concept of a classical shadow, a succinct classical description of a many-body quantum state that can be constructed in feasible quantum experiments and be used to predict many properties of the state. Extensive numerical experiments corroborate our theoretical results in a variety of scenarios, including Rydberg atom systems, 2D random Heisenberg models, symmetry-protected topological phases, and topologically ordered phases.
Information-theoretic bounds on quantum advantage in machine learning
Jan 07, 2021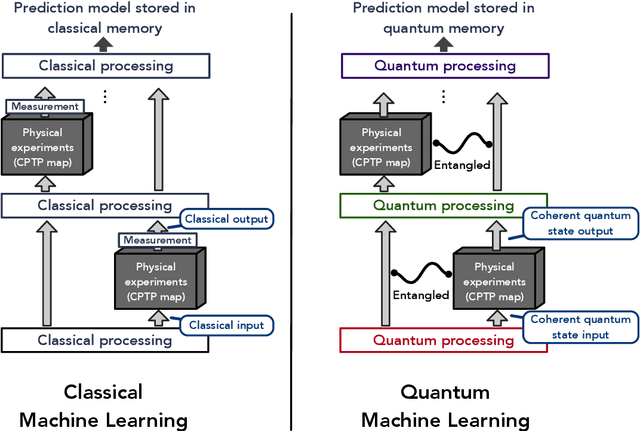
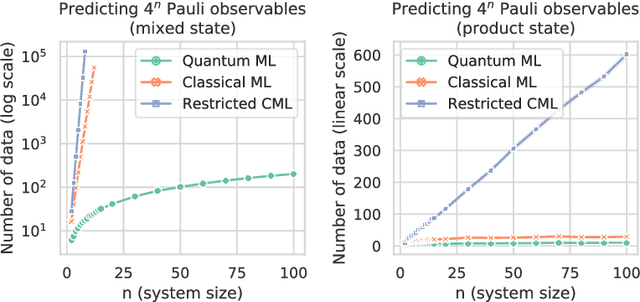
Abstract:We study the complexity of training classical and quantum machine learning (ML) models for predicting outcomes of physical experiments. The experiments depend on an input parameter $x$ and involve the execution of a (possibly unknown) quantum process $\mathcal{E}$. Our figure of merit is the number of runs of $\mathcal{E}$ during training, disregarding other measures of runtime. A classical ML model performs a measurement and records the classical outcome after each run of $\mathcal{E}$, while a quantum ML model can access $\mathcal{E}$ coherently to acquire quantum data; the classical or quantum data is then used to predict outcomes of future experiments. We prove that, for any input distribution $\mathcal{D}(x)$, a classical ML model can provide accurate predictions on average by accessing $\mathcal{E}$ a number of times comparable to the optimal quantum ML model. In contrast, for achieving accurate prediction on all inputs, we show that exponential quantum advantage is possible for certain tasks. For example, to predict expectation values of all Pauli observables in an $n$-qubit system $\rho$, we present a quantum ML model using only $\mathcal{O}(n)$ copies of $\rho$ and prove that classical ML models require $2^{\Omega(n)}$ copies.
Power of data in quantum machine learning
Nov 03, 2020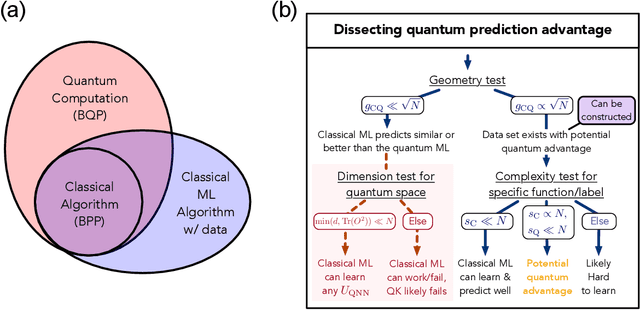
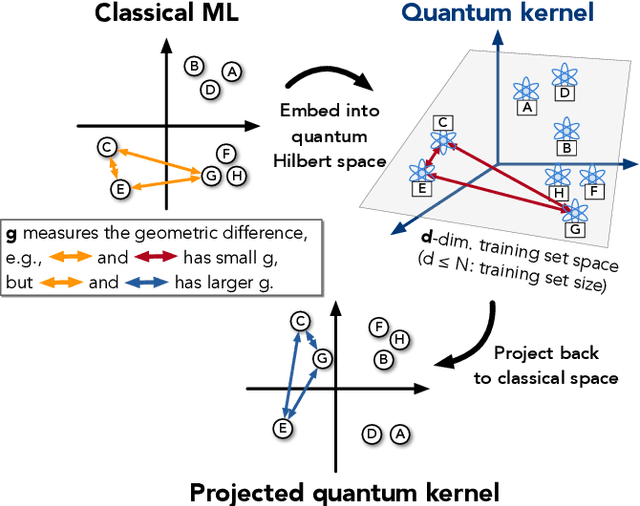
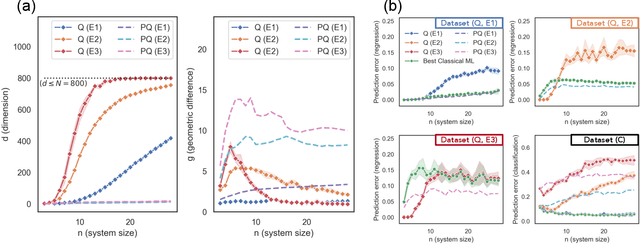
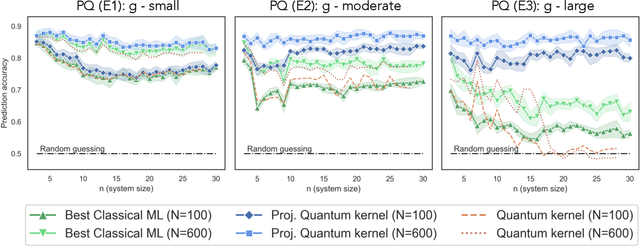
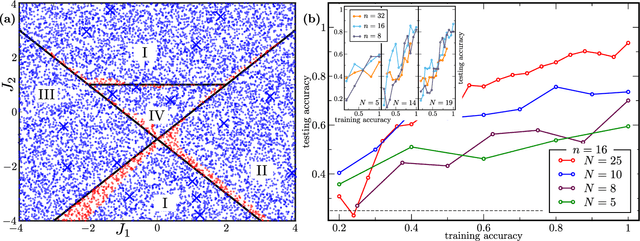
Abstract:The use of quantum computing for machine learning is among the most exciting prospective applications of quantum technologies. At the crux of excitement is the potential for quantum computers to perform some computations exponentially faster than their classical counterparts. However, a machine learning task where some data is provided can be considerably different than more commonly studied computational tasks. In this work, we show that some problems that are classically hard to compute can be predicted easily with classical machines that learn from data. We find that classical machines can often compete or outperform existing quantum models even on data sets generated by quantum evolution, especially at large system sizes. Using rigorous prediction error bounds as a foundation, we develop a methodology for assessing the potential for quantum advantage in prediction on learning tasks. We show how the use of exponentially large quantum Hilbert space in existing quantum models can result in significantly inferior prediction performance compared to classical machines. To circumvent the observed setbacks, we propose an improvement by projecting all quantum states to an approximate classical representation. The projected quantum model provides a simple and rigorous quantum speed-up for a recently proposed learning problem in the fault-tolerant regime. For more near-term quantum models, the projected versions demonstrate a significant prediction advantage over some classical models on engineered data sets in one of the largest numerical tests for gate-based quantum machine learning to date, up to 30 qubits.
Predicting Many Properties of a Quantum System from Very Few Measurements
Feb 18, 2020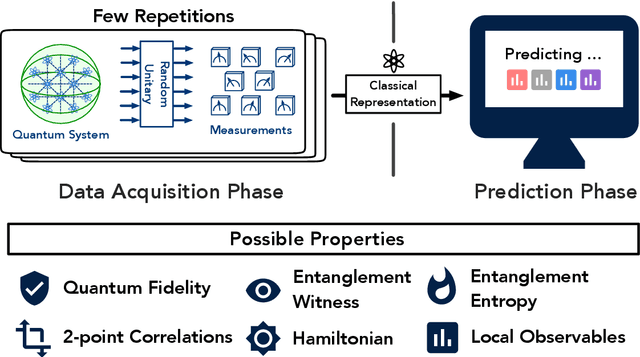

Abstract:Predicting properties of complex, large-scale quantum systems is essential for developing quantum technologies. We present an efficient method for constructing an approximate classical description of a quantum state using very few measurements of the state. This description, called a classical shadow, can be used to predict many different properties: order $\log M$ measurements suffice to accurately predict $M$ different functions of the state with high success probability. The number of measurements is independent of the system size, and saturates information-theoretic lower bounds. Moreover, target properties to predict can be selected after the measurements are completed. We support our theoretical findings with extensive numerical experiments. We apply classical shadows to predict quantum fidelities, entanglement entropies, two-point correlation functions, expectation values of local observables, and the energy variance of many-body local Hamiltonians, which allows applications to speedup variational quantum algorithms. The numerical results highlight the advantages of classical shadows relative to previously known methods.
Predicting Features of Quantum Systems using Classical Shadows
Aug 23, 2019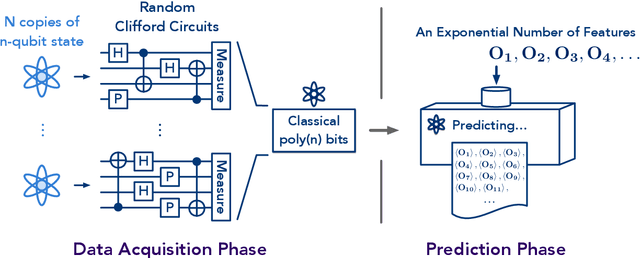
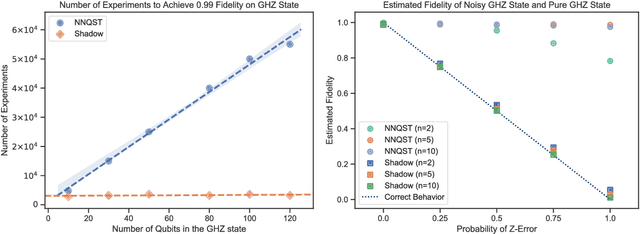
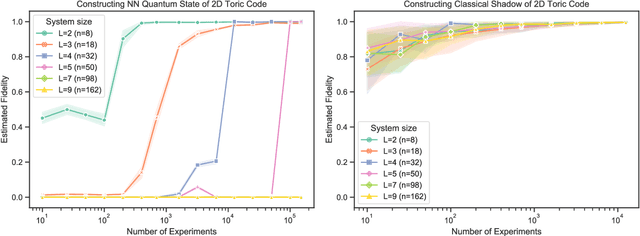
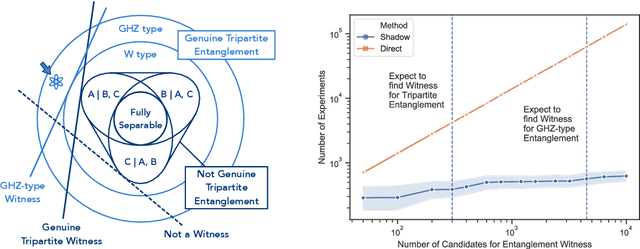
Abstract:Predicting features of complex, large-scale quantum systems is essential to the characterization and engineering of quantum architectures. We present an efficient approach for predicting a large number of linear features using classical shadows obtained from very few quantum measurements. This approach is guaranteed to accurately predict $M$ linear functions with bounded Hilbert-Schmidt norm from only $\log (M)$ measurement repetitions. This sampling rate is completely independent of the system size and saturates fundamental lower bounds from information theory. We support our theoretical findings with numerical experiments over a wide range of problem sizes (2 to 162 qubits). These highlight advantages compared to existing machine learning approaches.
FlowQA: Grasping Flow in History for Conversational Machine Comprehension
Oct 06, 2018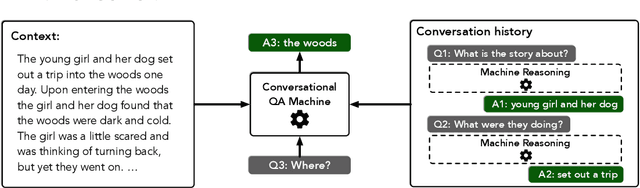
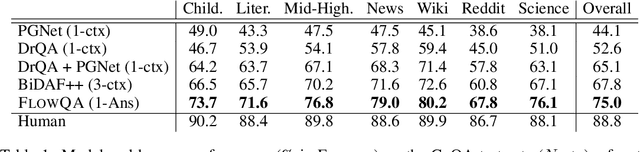
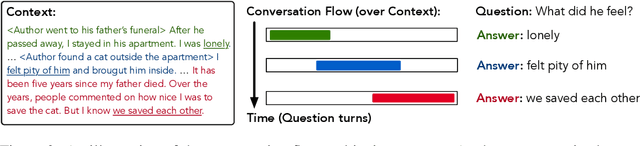

Abstract:Conversational machine comprehension requires a deep understanding of the conversation history. To enable traditional, single-turn models to encode the history comprehensively, we introduce Flow, a mechanism that can incorporate intermediate representations generated during the process of answering previous questions, through an alternating parallel processing structure. Compared to shallow approaches that concatenate previous questions/answers as input, Flow integrates the latent semantics of the conversation history more deeply. Our model, FlowQA, shows superior performance on two recently proposed conversational challenges (+7.2% F1 on CoQA and +4.0% on QuAC). The effectiveness of Flow also shows in other tasks. By reducing sequential instruction understanding to conversational machine comprehension, FlowQA outperforms the best models on all three domains in SCONE, with +1.8% to +4.4% improvement in accuracy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge