Expressive Power of ReLU and Step Networks under Floating-Point Operations

The study of the expressive power of neural networks has investigated the fundamental limits of neural networks. Most existing results assume real-valued inputs and parameters as well as exact operations during the evaluation of neural networks. However, neural networks are typically executed on computers that can only represent a tiny subset of the reals and apply inexact operations. In this work, we analyze the expressive power of neural networks under a more realistic setup: when we use floating-point numbers and operations. Our first set of results assumes floating-point operations where the significand of a float is represented by finite bits but its exponent can take any integer value. Under this setup, we show that neural networks using a binary threshold unit or ReLU can memorize any finite input/output pairs and can approximate any continuous function within a small error. We also show similar results on memorization and universal approximation when floating-point operations use finite bits for both significand and exponent; these results are applicable to many popular floating-point formats such as those defined in the IEEE 754 standard (e.g., 32-bit single-precision format) and bfloat16.

Training with Mixed-Precision Floating-Point Assignments

When training deep neural networks, keeping all tensors in high precision (e.g., 32-bit or even 16-bit floats) is often wasteful. However, keeping all tensors in low precision (e.g., 8-bit floats) can lead to unacceptable accuracy loss. Hence, it is important to use a precision assignment -- a mapping from all tensors (arising in training) to precision levels (high or low) -- that keeps most of the tensors in low precision and leads to sufficiently accurate models. We provide a technique that explores this memory-accuracy tradeoff by generating precision assignments that (i) use less memory and (ii) lead to more accurate models at the same time, compared to the precision assignments considered by prior work in low-precision floating-point training. Our method typically provides > 2x memory reduction over a baseline precision assignment while preserving training accuracy, and gives further reductions by trading off accuracy. Compared to other baselines which sometimes cause training to diverge, our method provides similar or better memory reduction while avoiding divergence.

On the Correctness of Automatic Differentiation for Neural Networks with Machine-Representable Parameters

Recent work has shown that automatic differentiation over the reals is almost always correct in a mathematically precise sense. However, actual programs work with machine-representable numbers (e.g., floating-point numbers), not reals. In this paper, we study the correctness of automatic differentiation when the parameter space of a neural network consists solely of machine-representable numbers. For a neural network with bias parameters, we prove that automatic differentiation is correct at all parameters where the network is differentiable. In contrast, it is incorrect at all parameters where the network is non-differentiable, since it never informs non-differentiability. To better understand this non-differentiable set of parameters, we prove a tight bound on its size, which is linear in the number of non-differentiabilities in activation functions, and provide a simple necessary and sufficient condition for a parameter to be in this set. We further prove that automatic differentiation always computes a Clarke subderivative, even on the non-differentiable set. We also extend these results to neural networks possibly without bias parameters.

Smoothness Analysis for Probabilistic Programs with Application to Optimised Variational Inference

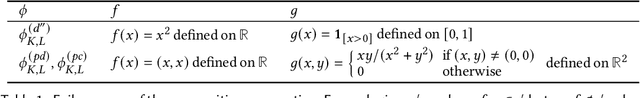
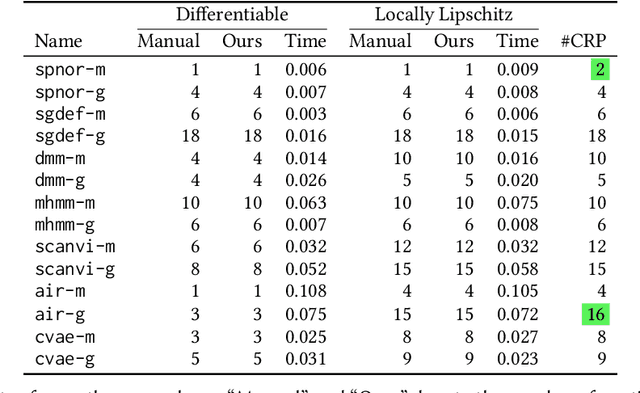
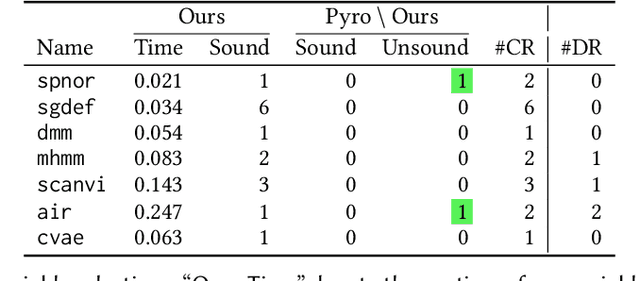
We present a static analysis for discovering differentiable or more generally smooth parts of a given probabilistic program, and show how the analysis can be used to improve the pathwise gradient estimator, one of the most popular methods for posterior inference and model learning. Our improvement increases the scope of the estimator from differentiable models to non-differentiable ones without requiring manual intervention of the user; the improved estimator automatically identifies differentiable parts of a given probabilistic program using our static analysis, and applies the pathwise gradient estimator to the identified parts while using a more general but less efficient estimator, called score estimator, for the rest of the program. Our analysis has a surprisingly subtle soundness argument, partly due to the misbehaviours of some target smoothness properties when viewed from the perspective of program analysis designers. For instance, some smoothness properties are not preserved by function composition, and this makes it difficult to analyse sequential composition soundly without heavily sacrificing precision. We formulate five assumptions on a target smoothness property, prove the soundness of our analysis under those assumptions, and show that our leading examples satisfy these assumptions. We also show that by using information from our analysis, our improved gradient estimator satisfies an important differentiability requirement and thus, under a mild regularity condition, computes the correct estimate on average, i.e., it returns an unbiased estimate. Our experiments with representative probabilistic programs in the Pyro language show that our static analysis is capable of identifying smooth parts of those programs accurately, and making our improved pathwise gradient estimator exploit all the opportunities for high performance in those programs.

On Correctness of Automatic Differentiation for Non-Differentiable Functions

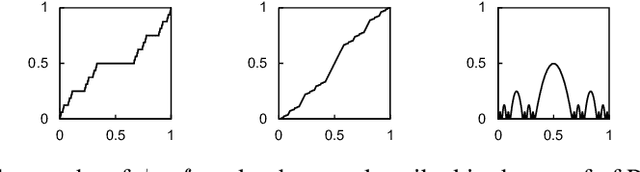
Differentiation lies at the core of many machine-learning algorithms, and is well-supported by popular autodiff systems, such as TensorFlow and PyTorch. Originally, these systems have been developed to compute derivatives of differentiable functions, but in practice, they are commonly applied to functions with non-differentiabilities. For instance, neural networks using ReLU define non-differentiable functions in general, but the gradients of losses involving those functions are computed using autodiff systems in practice. This status quo raises a natural question: are autodiff systems correct in any formal sense when they are applied to such non-differentiable functions? In this paper, we provide a positive answer to this question. Using counterexamples, we first point out flaws in often-used informal arguments, such as: non-differentiabilities arising in deep learning do not cause any issues because they form a measure-zero set. We then investigate a class of functions, called PAP functions, that includes nearly all (possibly non-differentiable) functions in deep learning nowadays. For these PAP functions, we propose a new type of derivatives, called intensional derivatives, and prove that these derivatives always exist and coincide with standard derivatives for almost all inputs. We also show that these intensional derivatives are what most autodiff systems compute or try to compute essentially. In this way, we formally establish the correctness of autodiff systems applied to non-differentiable functions.

Differentiable Algorithm for Marginalising Changepoints

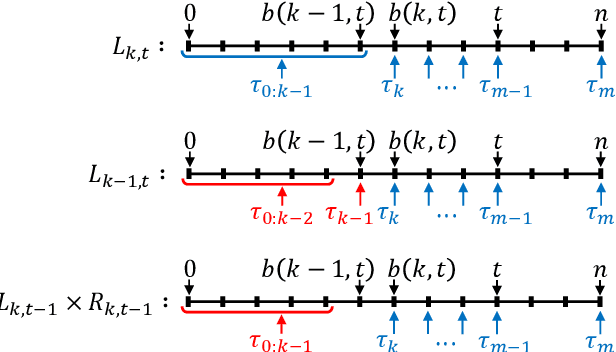
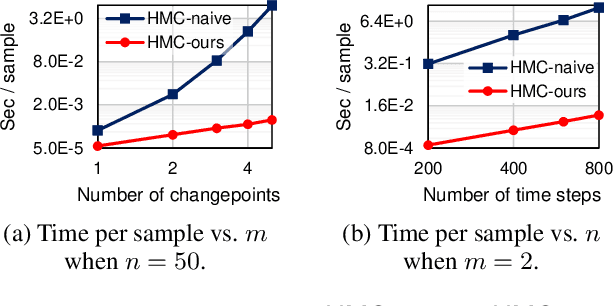
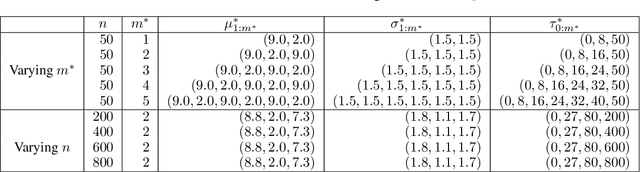
We present an algorithm for marginalising changepoints in time-series models that assume a fixed number of unknown changepoints. Our algorithm is differentiable with respect to its inputs, which are the values of latent random variables other than changepoints. Also, it runs in time O(mn) where n is the number of time steps and m the number of changepoints, an improvement over a naive marginalisation method with O(n^m) time complexity. We derive the algorithm by identifying quantities related to this marginalisation problem, showing that these quantities satisfy recursive relationships, and transforming the relationships to an algorithm via dynamic programming. Since our algorithm is differentiable, it can be applied to convert a model non-differentiable due to changepoints to a differentiable one, so that the resulting models can be analysed using gradient-based inference or learning techniques. We empirically show the effectiveness of our algorithm in this application by tackling the posterior inference problem on synthetic and real-world data.

Towards Verified Stochastic Variational Inference for Probabilistic Programs

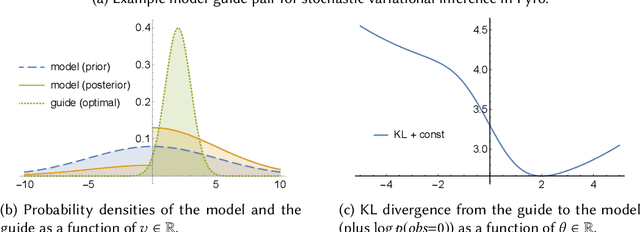
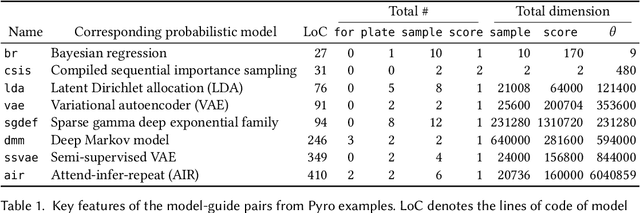
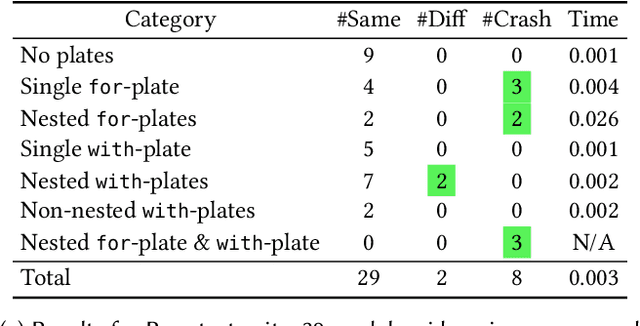
Probabilistic programming is the idea of writing models from statistics and machine learning using program notations and reasoning about these models using generic inference engines. Recently its combination with deep learning has been explored intensely, which led to the development of deep probabilistic programming languages. At the core of this development lie inference engines based on stochastic variational inference algorithms. When asked to find information about the posterior distribution of a model written in such a language, these algorithms convert this posterior-inference query into an optimisation problem and solve it approximately by a form of gradient ascent or descent. In this paper, we analyse one of the most fundamental and versatile variational inference algorithms, called score estimator or REINFORCE, using tools from denotational semantics and program analysis. We formally express what this algorithm does on models denoted by programs, and expose implicit assumptions made by the algorithm on the models. The violation of these assumptions may lead to an undefined optimisation objective or the loss of convergence guarantee of the optimisation process. We then describe rules for proving these assumptions, which can be automated by static program analyses. Some of our rules use nontrivial facts from continuous mathematics, and let us replace requirements about integrals in the assumptions, by conditions involving differentiation or boundedness, which are much easier to prove automatically. Following our general methodology, we have developed a static program analysis for the Pyro programming language that aims at discharging the assumption about what we call model-guide support match. Applied to the eight representative model-guide pairs from the Pyro webpage, our analysis finds a bug in two of these cases and shows that the assumptions are met in the others.

Reparameterization Gradient for Non-differentiable Models

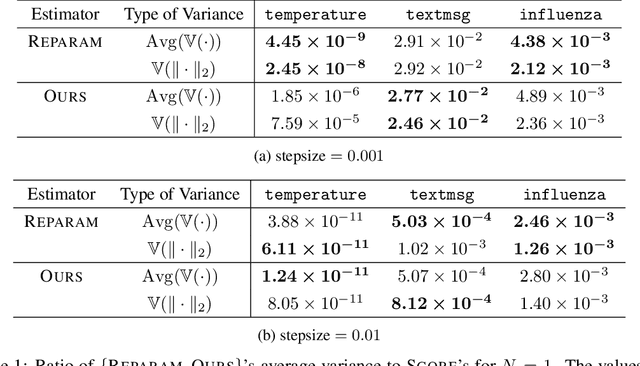
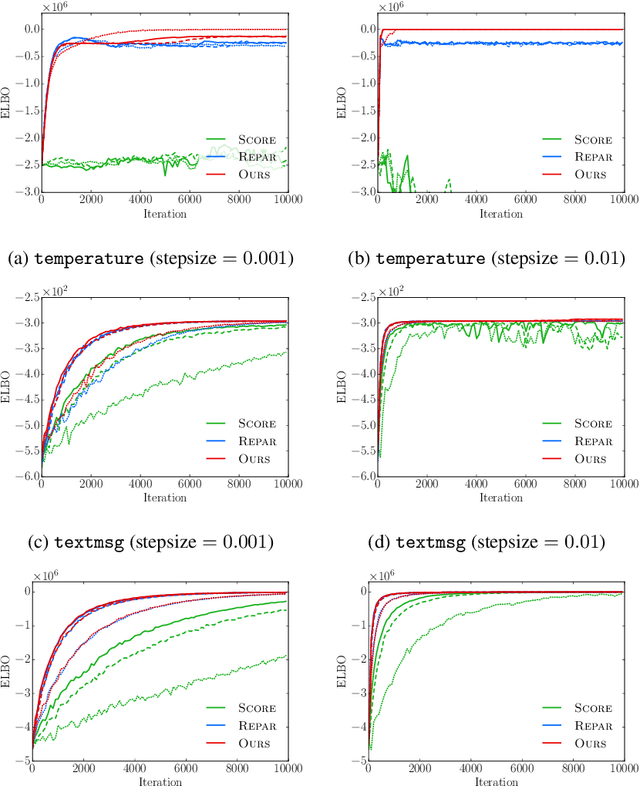
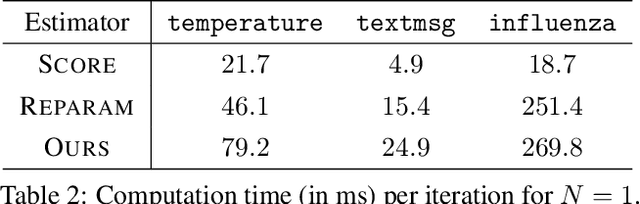
We present a new algorithm for stochastic variational inference that targets at models with non-differentiable densities. One of the key challenges in stochastic variational inference is to come up with a low-variance estimator of the gradient of a variational objective. We tackle the challenge by generalizing the reparameterization trick, one of the most effective techniques for addressing the variance issue for differentiable models, so that the trick works for non-differentiable models as well. Our algorithm splits the space of latent variables into regions where the density of the variables is differentiable, and their boundaries where the density may fail to be differentiable. For each differentiable region, the algorithm applies the standard reparameterization trick and estimates the gradient restricted to the region. For each potentially non-differentiable boundary, it uses a form of manifold sampling and computes the direction for variational parameters that, if followed, would increase the boundary's contribution to the variational objective. The sum of all the estimates becomes the gradient estimate of our algorithm. Our estimator enjoys the reduced variance of the reparameterization gradient while remaining unbiased even for non-differentiable models. The experiments with our preliminary implementation confirm the benefit of reduced variance and unbiasedness.