Deep neural networks with dependent weights: Gaussian Process mixture limit, heavy tails, sparsity and compressibility

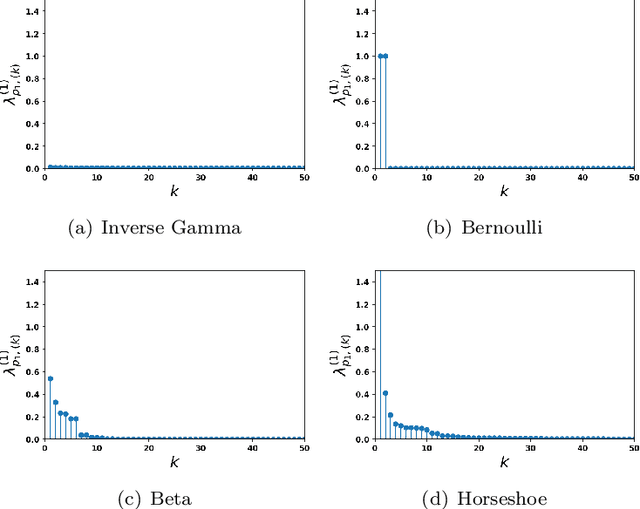
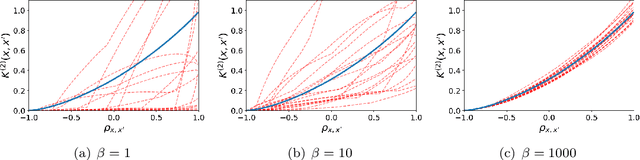
This article studies the infinite-width limit of deep feedforward neural networks whose weights are dependent, and modelled via a mixture of Gaussian distributions. Each hidden node of the network is assigned a nonnegative random variable that controls the variance of the outgoing weights of that node. We make minimal assumptions on these per-node random variables: they are iid and their sum, in each layer, converges to some finite random variable in the infinite-width limit. Under this model, we show that each layer of the infinite-width neural network can be characterised by two simple quantities: a non-negative scalar parameter and a L\'evy measure on the positive reals. If the scalar parameters are strictly positive and the L\'evy measures are trivial at all hidden layers, then one recovers the classical Gaussian process (GP) limit, obtained with iid Gaussian weights. More interestingly, if the L\'evy measure of at least one layer is non-trivial, we obtain a mixture of Gaussian processes (MoGP) in the large-width limit. The behaviour of the neural network in this regime is very different from the GP regime. One obtains correlated outputs, with non-Gaussian distributions, possibly with heavy tails. Additionally, we show that, in this regime, the weights are compressible, and feature learning is possible. Many sparsity-promoting neural network models can be recast as special cases of our approach, and we discuss their infinite-width limits; we also present an asymptotic analysis of the pruning error. We illustrate some of the benefits of the MoGP regime over the GP regime in terms of representation learning and compressibility on simulated, MNIST and Fashion MNIST datasets.

Non-exchangeable feature allocation models with sublinear growth of the feature sizes

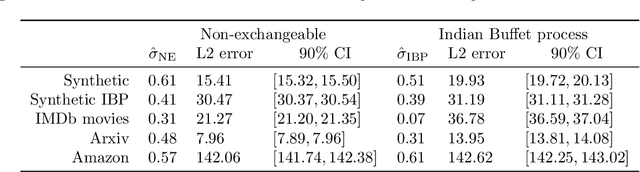
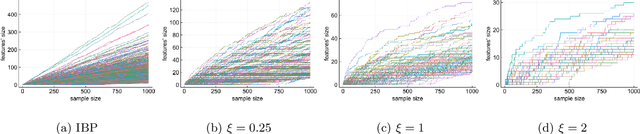
Feature allocation models are popular models used in different applications such as unsupervised learning or network modeling. In particular, the Indian buffet process is a flexible and simple one-parameter feature allocation model where the number of features grows unboundedly with the number of objects. The Indian buffet process, like most feature allocation models, satisfies a symmetry property of exchangeability: the distribution is invariant under permutation of the objects. While this property is desirable in some cases, it has some strong implications. Importantly, the number of objects sharing a particular feature grows linearly with the number of objects. In this article, we describe a class of non-exchangeable feature allocation models where the number of objects sharing a given feature grows sublinearly, where the rate can be controlled by a tuning parameter. We derive the asymptotic properties of the model, and show that such model provides a better fit and better predictive performances on various datasets.

A unified construction for series representations and finite approximations of completely random measures

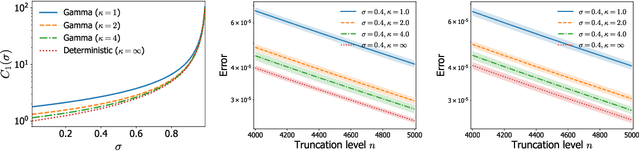
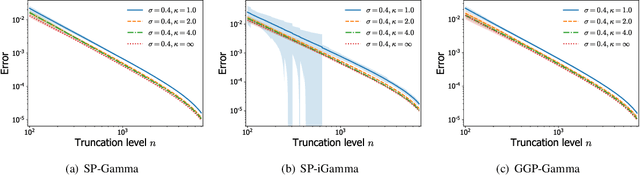
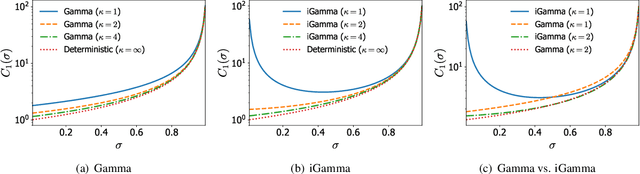
Infinite-activity completely random measures (CRMs) have become important building blocks of complex Bayesian nonparametric models. They have been successfully used in various applications such as clustering, density estimation, latent feature models, survival analysis or network science. Popular infinite-activity CRMs include the (generalized) gamma process and the (stable) beta process. However, except in some specific cases, exact simulation or scalable inference with these models is challenging and finite-dimensional approximations are often considered. In this work, we propose a general and unified framework to derive both series representations and finite-dimensional approximations of CRMs. Our framework can be seen as an extension of constructions based on size-biased sampling of Poisson point process [Perman1992]. It includes as special cases several known series representations as well as novel ones. In particular, we show that one can get novel series representations for the generalized gamma process and the stable beta process. We also provide some analysis of the truncation error.

Beyond the Chinese Restaurant and Pitman-Yor processes: Statistical Models with Double Power-law Behavior

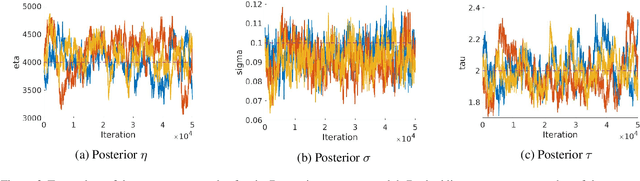
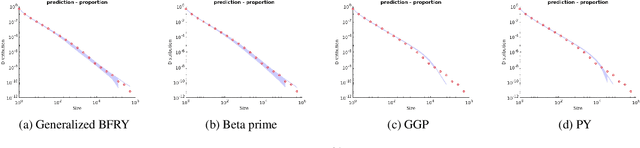
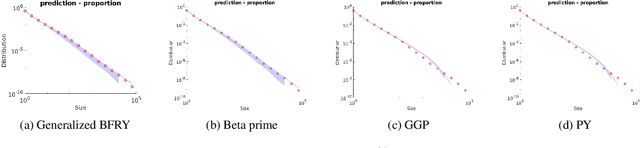
Bayesian nonparametric approaches, in particular the Pitman-Yor process and the associated two-parameter Chinese Restaurant process, have been successfully used in applications where the data exhibit a power-law behavior. Examples include natural language processing, natural images or networks. There is also growing empirical evidence that some datasets exhibit a two-regime power-law behavior: one regime for small frequencies, and a second regime, with a different exponent, for high frequencies. In this paper, we introduce a class of completely random measures which are doubly regularly-varying. Contrary to the Pitman-Yor process, we show that when completely random measures in this class are normalized to obtain random probability measures and associated random partitions, such partitions exhibit a double power-law behavior. We discuss in particular three models within this class: the beta prime process (Broderick et al. (2015, 2018), a novel process called generalized BFRY process, and a mixture construction. We derive efficient Markov chain Monte Carlo algorithms to estimate the parameters of these models. Finally, we show that the proposed models provide a better fit than the Pitman-Yor process on various datasets.

Modelling sparsity, heterogeneity, reciprocity and community structure in temporal interaction data

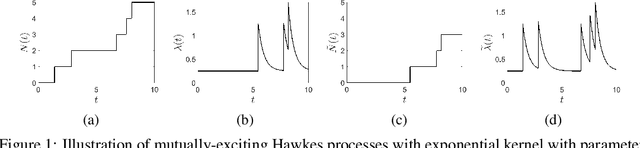
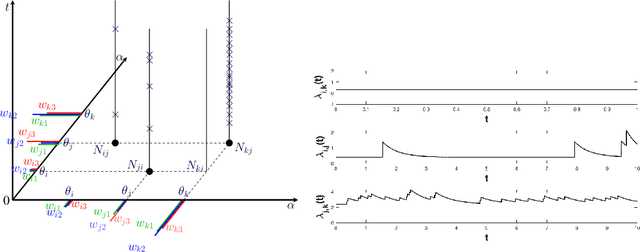
We propose a novel class of network models for temporal dyadic interaction data. Our goal is to capture a number of important features often observed in social interactions: sparsity, degree heterogeneity, community structure and reciprocity. We propose a family of models based on self-exciting Hawkes point processes in which events depend on the history of the process. The key component is the conditional intensity function of the Hawkes Process, which captures the fact that interactions may arise as a response to past interactions (reciprocity), or due to shared interests between individuals (community structure). In order to capture the sparsity and degree heterogeneity, the base (non time dependent) part of the intensity function builds on compound random measures following Todeschini et al. (2016). We conduct experiments on a variety of real-world temporal interaction data and show that the proposed model outperforms many competing approaches for link prediction, and leads to interpretable parameters.

A Bayesian model for sparse graphs with flexible degree distribution and overlapping community structure

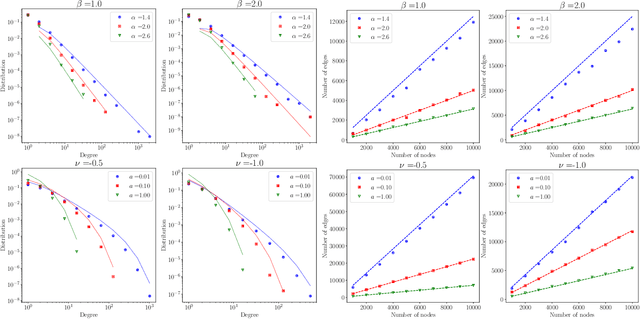
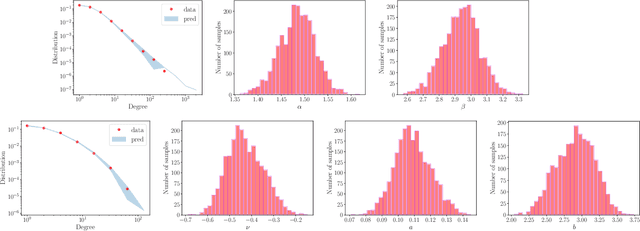
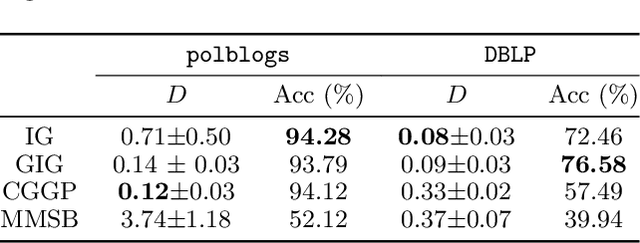
We consider a non-projective class of inhomogeneous random graph models with interpretable parameters and a number of interesting asymptotic properties. Using the results of Bollob\'as et al. [2007], we show that i) the class of models is sparse and ii) depending on the choice of the parameters, the model is either scale-free, with power-law exponent greater than 2, or with an asymptotic degree distribution which is power-law with exponential cut-off. We propose an extension of the model that can accommodate an overlapping community structure. Scalable posterior inference can be performed due to the specific choice of the link probability. We present experiments on five different real-world networks with up to 100,000 nodes and edges, showing that the model can provide a good fit to the degree distribution and recovers well the latent community structure.

Non-exchangeable random partition models for microclustering

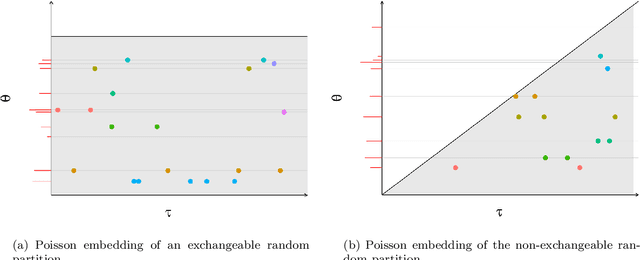
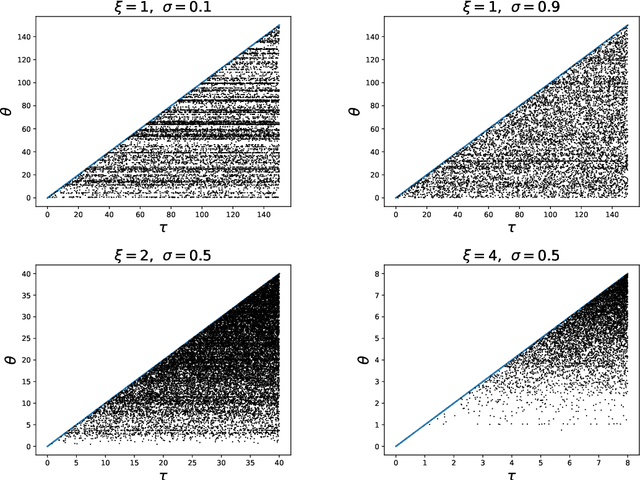
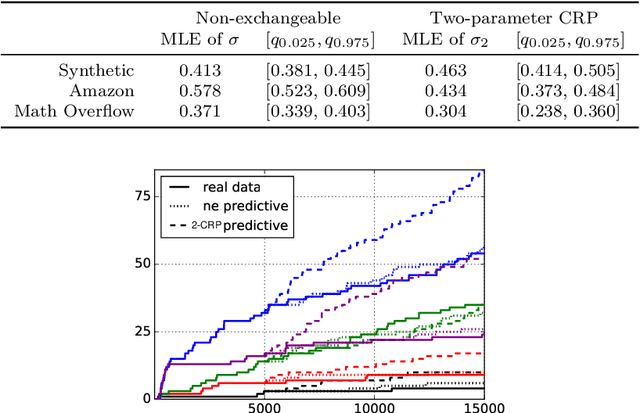
Many popular random partition models, such as the Chinese restaurant process and its two-parameter extension, fall in the class of exchangeable random partitions, and have found wide applicability in model-based clustering, population genetics, ecology or network analysis. While the exchangeability assumption is sensible in many cases, it has some strong implications. In particular, Kingman's representation theorem implies that the size of the clusters necessarily grows linearly with the sample size; this feature may be undesirable for some applications, as recently pointed out by Miller et al. (2015). We present here a flexible class of non-exchangeable random partition models which are able to generate partitions whose cluster sizes grow sublinearly with the sample size, and where the growth rate is controlled by one parameter. Along with this result, we provide the asymptotic behaviour of the number of clusters of a given size, and show that the model can exhibit a power-law behavior, controlled by another parameter. The construction is based on completely random measures and a Poisson embedding of the random partition, and inference is performed using a Sequential Monte Carlo algorithm. Additionally, we show how the model can also be directly used to generate sparse multigraphs with power-law degree distributions and degree sequences with sublinear growth. Finally, experiments on real datasets emphasize the usefulness of the approach compared to a two-parameter Chinese restaurant process.

Sequential Dirichlet Process Mixtures of Multivariate Skew t-distributions for Model-based Clustering of Flow Cytometry Data

Flow cytometry is a high-throughput technology used to quantify multiple surface and intracellular markers at the level of a single cell. This enables to identify cell sub-types, and to determine their relative proportions. Improvements of this technology allow to describe millions of individual cells from a blood sample using multiple markers. This results in high-dimensional datasets, whose manual analysis is highly time-consuming and poorly reproducible. While several methods have been developed to perform automatic recognition of cell populations, most of them treat and analyze each sample independently. However, in practice, individual samples are rarely independent (e.g. longitudinal studies). Here, we propose to use a Bayesian nonparametric approach with Dirichlet process mixture (DPM) of multivariate skew $t$-distributions to perform model based clustering of flow-cytometry data. DPM models directly estimate the number of cell populations from the data, avoiding model selection issues, and skew $t$-distributions provides robustness to outliers and non-elliptical shape of cell populations. To accommodate repeated measurements, we propose a sequential strategy relying on a parametric approximation of the posterior. We illustrate the good performance of our method on simulated data, on an experimental benchmark dataset, and on new longitudinal data from the DALIA-1 trial which evaluates a therapeutic vaccine against HIV. On the benchmark dataset, the sequential strategy outperforms all other methods evaluated, and similarly, leads to improved performance on the DALIA-1 data. We have made the method available for the community in the R package NPflow.

Exchangeable Random Measures for Sparse and Modular Graphs with Overlapping Communities

We propose a novel statistical model for sparse networks with overlapping community structure. The model is based on representing the graph as an exchangeable point process, and naturally generalizes existing probabilistic models with overlapping block-structure to the sparse regime. Our construction builds on vectors of completely random measures, and has interpretable parameters, each node being assigned a vector representing its level of affiliation to some latent communities. We develop methods for simulating this class of random graphs, as well as to perform posterior inference. We show that the proposed approach can recover interpretable structure from two real-world networks and can handle graphs with thousands of nodes and tens of thousands of edges.

Sparse graphs using exchangeable random measures

Statistical network modeling has focused on representing the graph as a discrete structure, namely the adjacency matrix, and considering the exchangeability of this array. In such cases, the Aldous-Hoover representation theorem (Aldous, 1981;Hoover, 1979} applies and informs us that the graph is necessarily either dense or empty. In this paper, we instead consider representing the graph as a measure on $\mathbb{R}_+^2$. For the associated definition of exchangeability in this continuous space, we rely on the Kallenberg representation theorem (Kallenberg, 2005). We show that for certain choices of such exchangeable random measures underlying our graph construction, our network process is sparse with power-law degree distribution. In particular, we build on the framework of completely random measures (CRMs) and use the theory associated with such processes to derive important network properties, such as an urn representation for our analysis and network simulation. Our theoretical results are explored empirically and compared to common network models. We then present a Hamiltonian Monte Carlo algorithm for efficient exploration of the posterior distribution and demonstrate that we are able to recover graphs ranging from dense to sparse--and perform associated tests--based on our flexible CRM-based formulation. We explore network properties in a range of real datasets, including Facebook social circles, a political blogosphere, protein networks, citation networks, and world wide web networks, including networks with hundreds of thousands of nodes and millions of edges.