Optimal Algorithms for Augmented Testing of Discrete Distributions

We consider the problem of hypothesis testing for discrete distributions. In the standard model, where we have sample access to an underlying distribution $p$, extensive research has established optimal bounds for uniformity testing, identity testing (goodness of fit), and closeness testing (equivalence or two-sample testing). We explore these problems in a setting where a predicted data distribution, possibly derived from historical data or predictive machine learning models, is available. We demonstrate that such a predictor can indeed reduce the number of samples required for all three property testing tasks. The reduction in sample complexity depends directly on the predictor's quality, measured by its total variation distance from $p$. A key advantage of our algorithms is their adaptability to the precision of the prediction. Specifically, our algorithms can self-adjust their sample complexity based on the accuracy of the available prediction, operating without any prior knowledge of the estimation's accuracy (i.e. they are consistent). Additionally, we never use more samples than the standard approaches require, even if the predictions provide no meaningful information (i.e. they are also robust). We provide lower bounds to indicate that the improvements in sample complexity achieved by our algorithms are information-theoretically optimal. Furthermore, experimental results show that the performance of our algorithms on real data significantly exceeds our worst-case guarantees for sample complexity, demonstrating the practicality of our approach.

Exponentially Improving the Complexity of Simulating the Weisfeiler-Lehman Test with Graph Neural Networks

Recent work shows that the expressive power of Graph Neural Networks (GNNs) in distinguishing non-isomorphic graphs is exactly the same as that of the Weisfeiler-Lehman (WL) graph test. In particular, they show that the WL test can be simulated by GNNs. However, those simulations involve neural networks for the 'combine' function of size polynomial or even exponential in the number of graph nodes $n$, as well as feature vectors of length linear in $n$. We present an improved simulation of the WL test on GNNs with \emph{exponentially} lower complexity. In particular, the neural network implementing the combine function in each node has only a polylogarithmic number of parameters in $n$, and the feature vectors exchanged by the nodes of GNN consists of only $O(\log n)$ bits. We also give logarithmic lower bounds for the feature vector length and the size of the neural networks, showing the (near)-optimality of our construction.

Testing distributional assumptions of learning algorithms

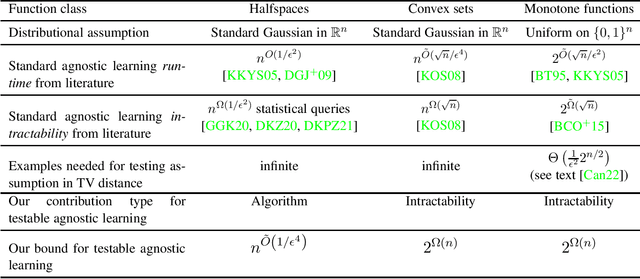
There are many important high dimensional function classes that have fast agnostic learning algorithms when strong assumptions on the distribution of examples can be made, such as Gaussianity or uniformity over the domain. But how can one be sufficiently confident that the data indeed satisfies the distributional assumption, so that one can trust in the output quality of the agnostic learning algorithm? We propose a model by which to systematically study the design of tester-learner pairs $(\mathcal{A},\mathcal{T})$, such that if the distribution on examples in the data passes the tester $\mathcal{T}$ then one can safely trust the output of the agnostic learner $\mathcal{A}$ on the data. To demonstrate the power of the model, we apply it to the classical problem of agnostically learning halfspaces under the standard Gaussian distribution and present a tester-learner pair with a combined run-time of $n^{\tilde{O}(1/\epsilon^4)}$. This qualitatively matches that of the best known ordinary agnostic learning algorithms for this task. In contrast, finite sample Gaussian distribution testers do not exist for the $L_1$ and EMD distance measures. A key step in the analysis is a novel characterization of concentration and anti-concentration properties of a distribution whose low-degree moments approximately match those of a Gaussian. We also use tools from polynomial approximation theory. In contrast, we show strong lower bounds on the combined run-times of tester-learner pairs for the problems of agnostically learning convex sets under the Gaussian distribution and for monotone Boolean functions under the uniform distribution over $\{0,1\}^n$. Through these lower bounds we exhibit natural problems where there is a dramatic gap between standard agnostic learning run-time and the run-time of the best tester-learner pair.

Triangle and Four Cycle Counting with Predictions in Graph Streams

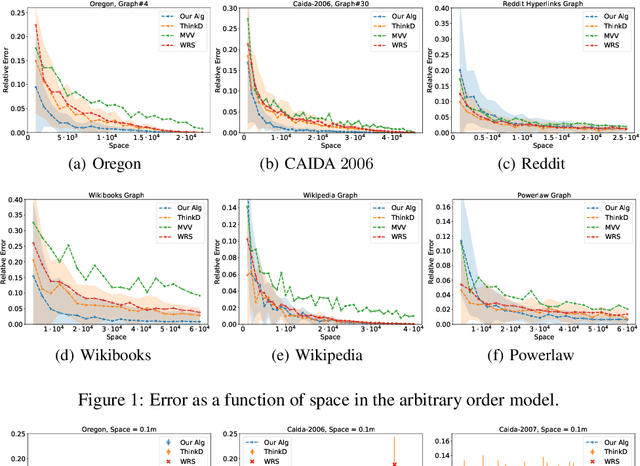
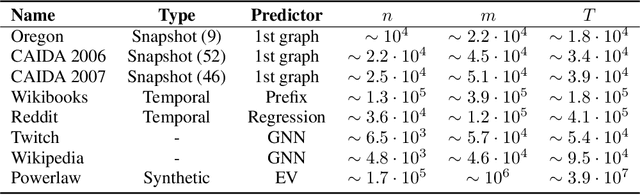
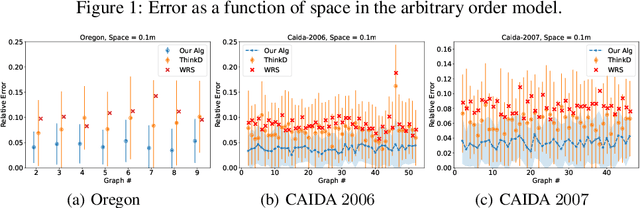
We propose data-driven one-pass streaming algorithms for estimating the number of triangles and four cycles, two fundamental problems in graph analytics that are widely studied in the graph data stream literature. Recently, (Hsu 2018) and (Jiang 2020) applied machine learning techniques in other data stream problems, using a trained oracle that can predict certain properties of the stream elements to improve on prior "classical" algorithms that did not use oracles. In this paper, we explore the power of a "heavy edge" oracle in multiple graph edge streaming models. In the adjacency list model, we present a one-pass triangle counting algorithm improving upon the previous space upper bounds without such an oracle. In the arbitrary order model, we present algorithms for both triangle and four cycle estimation with fewer passes and the same space complexity as in previous algorithms, and we show several of these bounds are optimal. We analyze our algorithms under several noise models, showing that the algorithms perform well even when the oracle errs. Our methodology expands upon prior work on "classical" streaming algorithms, as previous multi-pass and random order streaming algorithms can be seen as special cases of our algorithms, where the first pass or random order was used to implement the heavy edge oracle. Lastly, our experiments demonstrate advantages of the proposed method compared to state-of-the-art streaming algorithms.

Learning-based Support Estimation in Sublinear Time

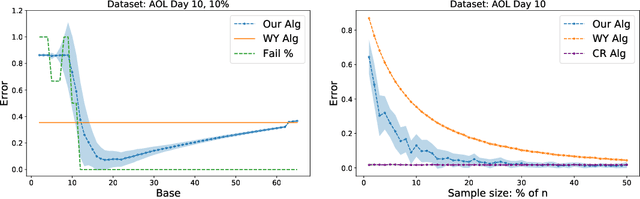
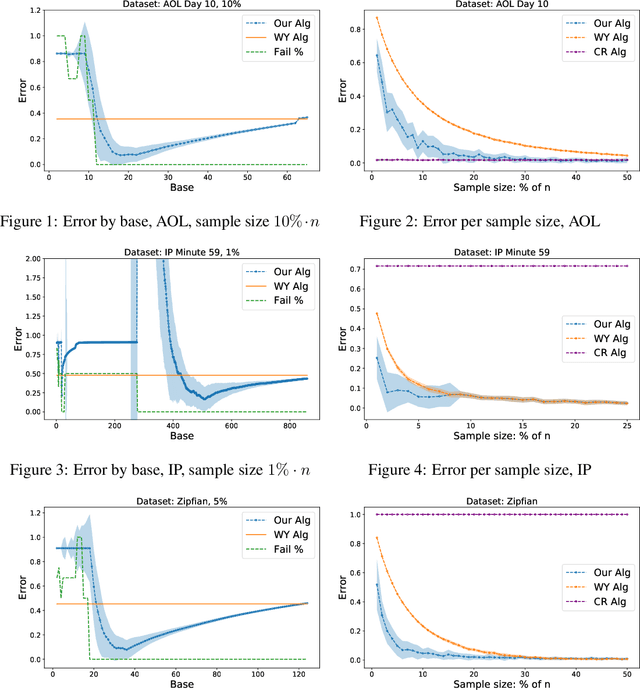
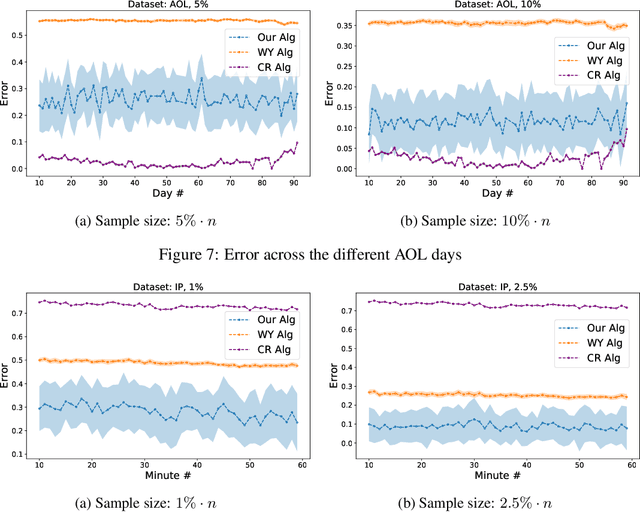
We consider the problem of estimating the number of distinct elements in a large data set (or, equivalently, the support size of the distribution induced by the data set) from a random sample of its elements. The problem occurs in many applications, including biology, genomics, computer systems and linguistics. A line of research spanning the last decade resulted in algorithms that estimate the support up to $ \pm \varepsilon n$ from a sample of size $O(\log^2(1/\varepsilon) \cdot n/\log n)$, where $n$ is the data set size. Unfortunately, this bound is known to be tight, limiting further improvements to the complexity of this problem. In this paper we consider estimation algorithms augmented with a machine-learning-based predictor that, given any element, returns an estimation of its frequency. We show that if the predictor is correct up to a constant approximation factor, then the sample complexity can be reduced significantly, to \[ \ \log (1/\varepsilon) \cdot n^{1-\Theta(1/\log(1/\varepsilon))}. \] We evaluate the proposed algorithms on a collection of data sets, using the neural-network based estimators from {Hsu et al, ICLR'19} as predictors. Our experiments demonstrate substantial (up to 3x) improvements in the estimation accuracy compared to the state of the art algorithm.

Testing Tail Weight of a Distribution Via Hazard Rate

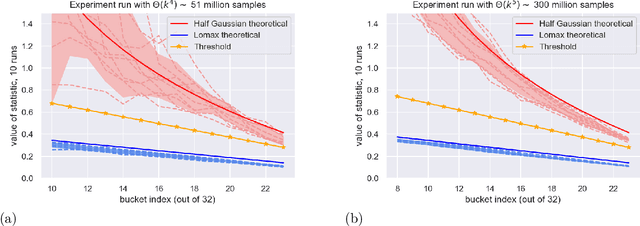
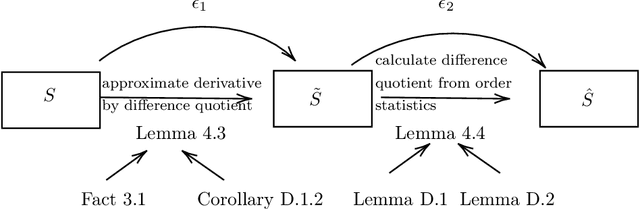
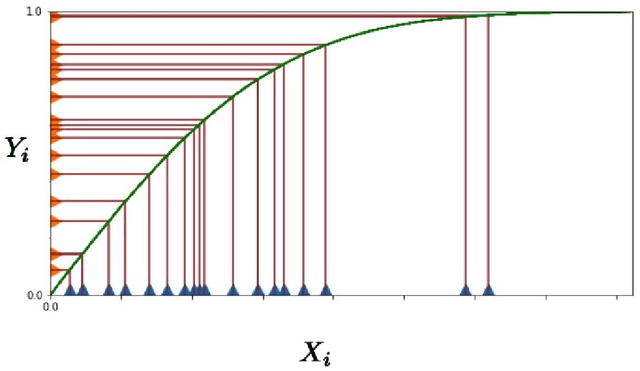
Understanding the shape of a distribution of data is of interest to people in a great variety of fields, as it may affect the types of algorithms used for that data. Given samples from a distribution, we seek to understand how many elements appear infrequently, that is, to characterize the tail of the distribution. We develop an algorithm based on a careful bucketing scheme that distinguishes heavy-tailed distributions from non-heavy-tailed ones via a definition based on the hazard rate under some natural smoothness and ordering assumptions. We verify our theoretical results empirically.

Online Page Migration with ML Advice

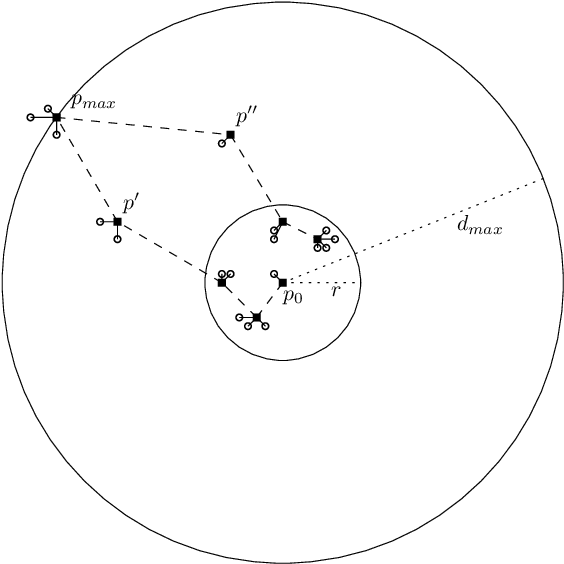
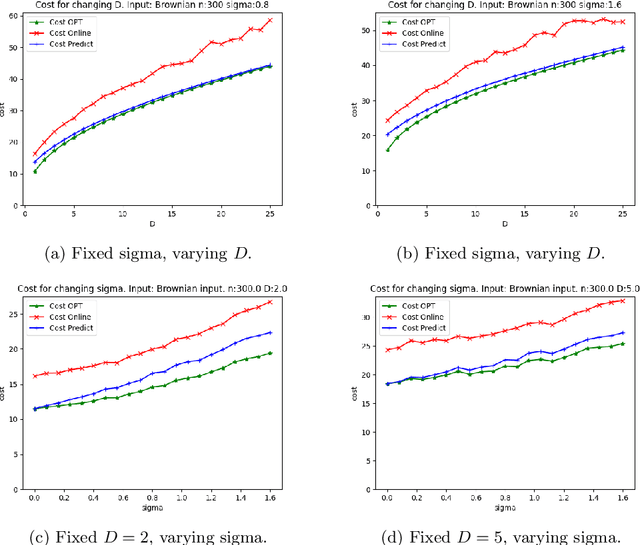
We consider online algorithms for the {\em page migration problem} that use predictions, potentially imperfect, to improve their performance. The best known online algorithms for this problem, due to Westbrook'94 and Bienkowski et al'17, have competitive ratios strictly bounded away from 1. In contrast, we show that if the algorithm is given a prediction of the input sequence, then it can achieve a competitive ratio that tends to $1$ as the prediction error rate tends to $0$. Specifically, the competitive ratio is equal to $1+O(q)$, where $q$ is the prediction error rate. We also design a ``fallback option'' that ensures that the competitive ratio of the algorithm for {\em any} input sequence is at most $O(1/q)$. Our result adds to the recent body of work that uses machine learning to improve the performance of ``classic'' algorithms.

Testing Mixtures of Discrete Distributions

There has been significant study on the sample complexity of testing properties of distributions over large domains. For many properties, it is known that the sample complexity can be substantially smaller than the domain size. For example, over a domain of size $n$, distinguishing the uniform distribution from distributions that are far from uniform in $\ell_1$-distance uses only $O(\sqrt{n})$ samples. However, the picture is very different in the presence of arbitrary noise, even when the amount of noise is quite small. In this case, one must distinguish if samples are coming from a distribution that is $\epsilon$-close to uniform from the case where the distribution is $(1-\epsilon)$-far from uniform. The latter task requires nearly linear in $n$ samples [Valiant 2008, Valian and Valiant 2011]. In this work, we present a noise model that on one hand is more tractable for the testing problem, and on the other hand represents a rich class of noise families. In our model, the noisy distribution is a mixture of the original distribution and noise, where the latter is known to the tester either explicitly or via sample access; the form of the noise is also known a priori. Focusing on the identity and closeness testing problems leads to the following mixture testing question: Given samples of distributions $p, q_1,q_2$, can we test if $p$ is a mixture of $q_1$ and $q_2$? We consider this general question in various scenarios that differ in terms of how the tester can access the distributions, and show that indeed this problem is more tractable. Our results show that the sample complexity of our testers are exactly the same as for the classical non-mixture case.

Towards Testing Monotonicity of Distributions Over General Posets

In this work, we consider the sample complexity required for testing the monotonicity of distributions over partial orders. A distribution $p$ over a poset is monotone if, for any pair of domain elements $x$ and $y$ such that $x \preceq y$, $p(x) \leq p(y)$. To understand the sample complexity of this problem, we introduce a new property called bigness over a finite domain, where the distribution is $T$-big if the minimum probability for any domain element is at least $T$. We establish a lower bound of $\Omega(n/\log n)$ for testing bigness of distributions on domains of size $n$. We then build on these lower bounds to give $\Omega(n/\log{n})$ lower bounds for testing monotonicity over a matching poset of size $n$ and significantly improved lower bounds over the hypercube poset. We give sublinear sample complexity bounds for testing bigness and for testing monotonicity over the matching poset. We then give a number of tools for analyzing upper bounds on the sample complexity of the monotonicity testing problem.

Sampling Correctors

In many situations, sample data is obtained from a noisy or imperfect source. In order to address such corruptions, this paper introduces the concept of a sampling corrector. Such algorithms use structure that the distribution is purported to have, in order to allow one to make "on-the-fly" corrections to samples drawn from probability distributions. These algorithms then act as filters between the noisy data and the end user. We show connections between sampling correctors, distribution learning algorithms, and distribution property testing algorithms. We show that these connections can be utilized to expand the applicability of known distribution learning and property testing algorithms as well as to achieve improved algorithms for those tasks. As a first step, we show how to design sampling correctors using proper learning algorithms. We then focus on the question of whether algorithms for sampling correctors can be more efficient in terms of sample complexity than learning algorithms for the analogous families of distributions. When correcting monotonicity, we show that this is indeed the case when also granted query access to the cumulative distribution function. We also obtain sampling correctors for monotonicity without this stronger type of access, provided that the distribution be originally very close to monotone (namely, at a distance $O(1/\log^2 n)$). In addition to that, we consider a restricted error model that aims at capturing "missing data" corruptions. In this model, we show that distributions that are close to monotone have sampling correctors that are significantly more efficient than achievable by the learning approach. We also consider the question of whether an additional source of independent random bits is required by sampling correctors to implement the correction process.