Learning Non-Markovian Quantum Noise from Moiré-Enhanced Swap Spectroscopy with Deep Evolutionary Algorithm

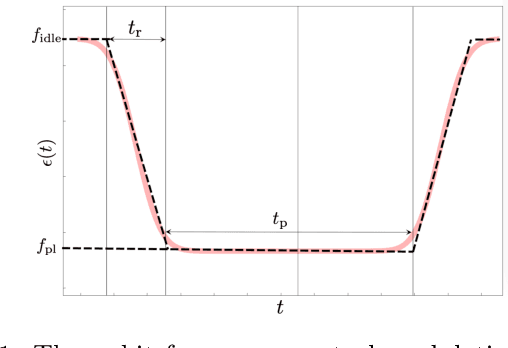
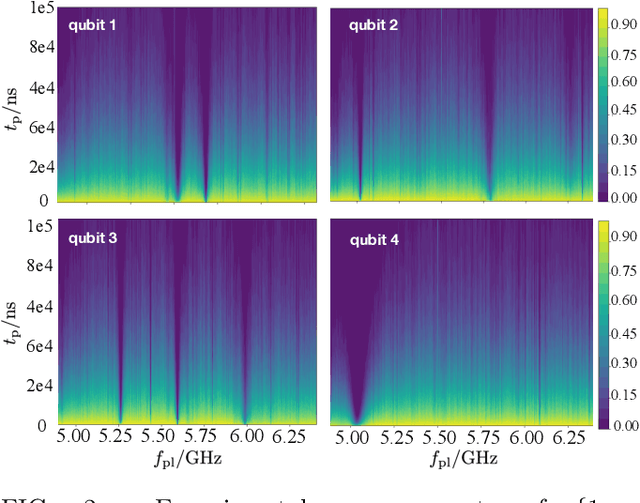
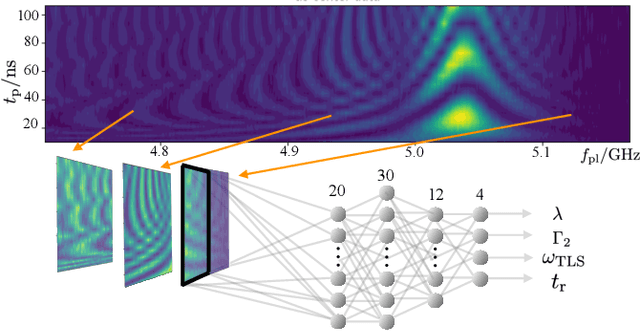
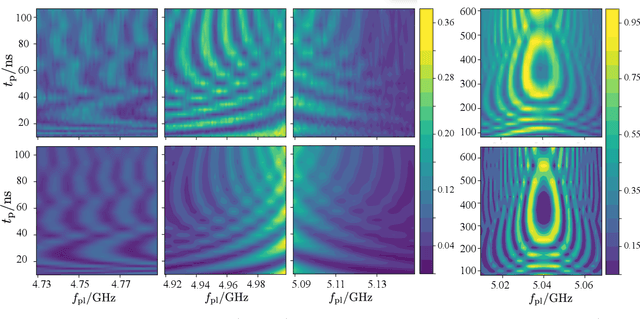
Two-level-system (TLS) defects in amorphous dielectrics are a major source of noise and decoherence in solid-state qubits. Gate-dependent non-Markovian errors caused by TLS-qubit coupling are detrimental to fault-tolerant quantum computation and have not been rigorously treated in the existing literature. In this work, we derive the non-Markovian dynamics between TLS and qubits during a SWAP-like two-qubit gate and the associated average gate fidelity for frequency-tunable Transmon qubits. This gate dependent error model facilitates using qubits as sensors to simultaneously learn practical imperfections in both the qubit's environment and control waveforms. We combine the-state-of-art machine learning algorithm with Moir\'{e}-enhanced swap spectroscopy to achieve robust learning using noisy experimental data. Deep neural networks are used to represent the functional map from experimental data to TLS parameters and are trained through an evolutionary algorithm. Our method achieves the highest learning efficiency and robustness against experimental imperfections to-date, representing an important step towards in-situ quantum control optimization over environmental and control defects.

Learning to learn with quantum neural networks via classical neural networks

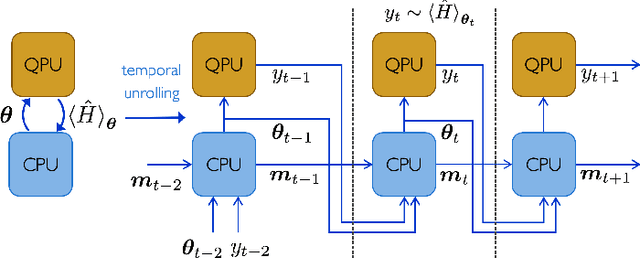
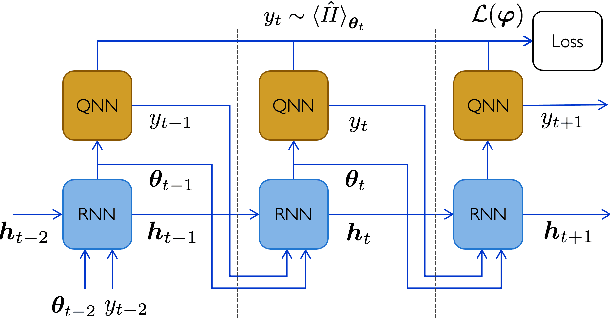
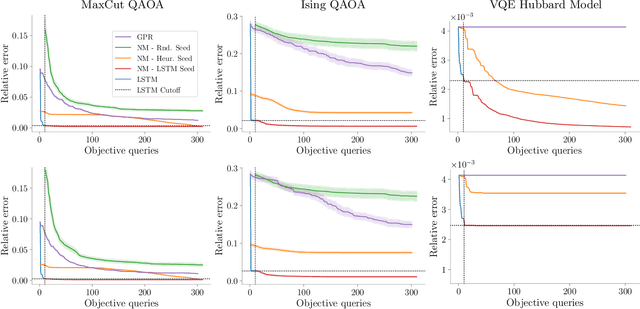
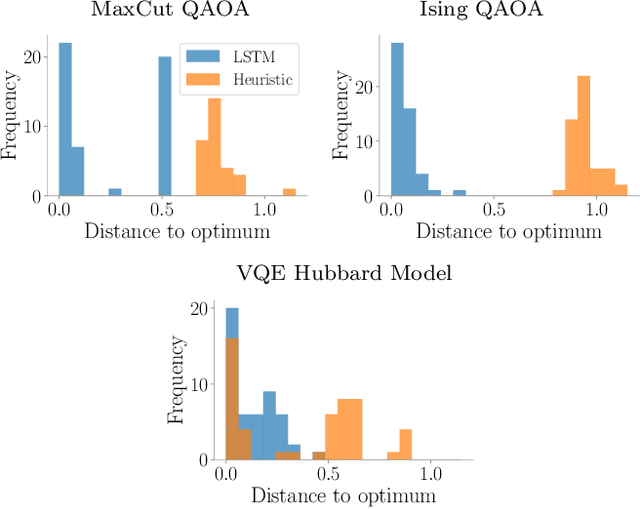
Quantum Neural Networks (QNNs) are a promising variational learning paradigm with applications to near-term quantum processors, however they still face some significant challenges. One such challenge is finding good parameter initialization heuristics that ensure rapid and consistent convergence to local minima of the parameterized quantum circuit landscape. In this work, we train classical neural networks to assist in the quantum learning process, also know as meta-learning, to rapidly find approximate optima in the parameter landscape for several classes of quantum variational algorithms. Specifically, we train classical recurrent neural networks to find approximately optimal parameters within a small number of queries of the cost function for the Quantum Approximate Optimization Algorithm (QAOA) for MaxCut, QAOA for Sherrington-Kirkpatrick Ising model, and for a Variational Quantum Eigensolver for the Hubbard model. By initializing other optimizers at parameter values suggested by the classical neural network, we demonstrate a significant improvement in the total number of optimization iterations required to reach a given accuracy. We further demonstrate that the optimization strategies learned by the neural network generalize well across a range of problem instance sizes. This opens up the possibility of training on small, classically simulatable problem instances, in order to initialize larger, classically intractably simulatable problem instances on quantum devices, thereby significantly reducing the number of required quantum-classical optimization iterations.

Quantum-Assisted Genetic Algorithm

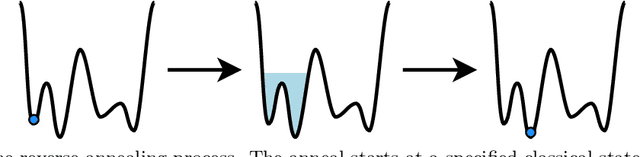
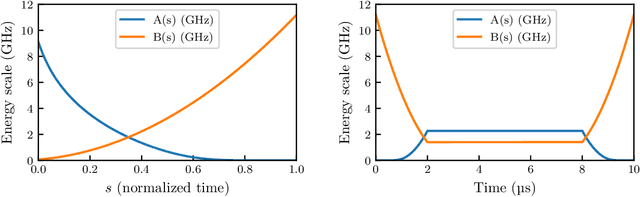
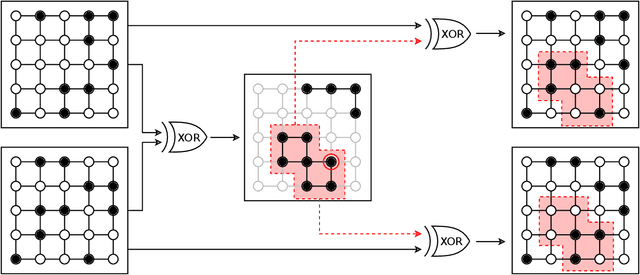
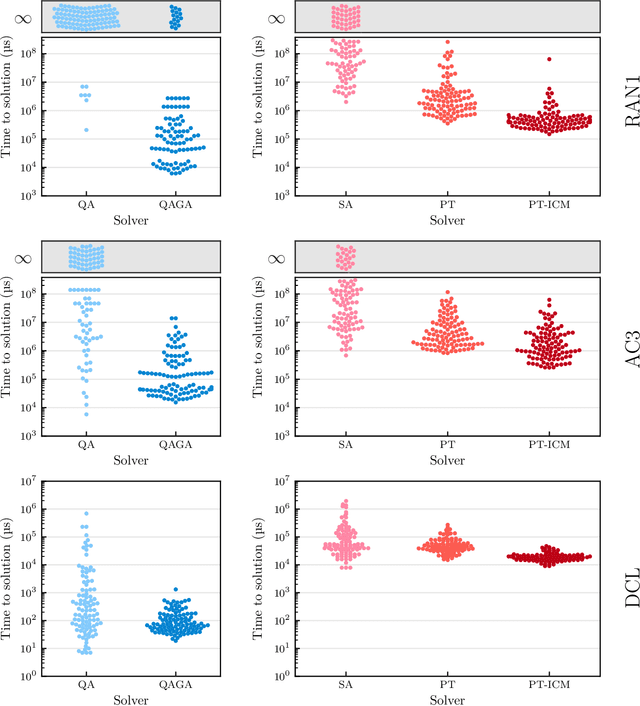
Genetic algorithms, which mimic evolutionary processes to solve optimization problems, can be enhanced by using powerful semi-local search algorithms as mutation operators. Here, we introduce reverse quantum annealing, a class of quantum evolutions that can be used for performing families of quasi-local or quasi-nonlocal search starting from a classical state, as novel sources of mutations. Reverse annealing enables the development of genetic algorithms that use quantum fluctuation for mutations and classical mechanisms for the crossovers -- we refer to these as Quantum-Assisted Genetic Algorithms (QAGAs). We describe a QAGA and present experimental results using a D-Wave 2000Q quantum annealing processor. On a set of spin-glass inputs, standard (forward) quantum annealing finds good solutions very quickly but struggles to find global optima. In contrast, our QAGA proves effective at finding global optima for these inputs. This successful interplay of non-local classical and quantum fluctuations could provide a promising step toward practical applications of Noisy Intermediate-Scale Quantum (NISQ) devices for heuristic discrete optimization.

Universal discriminative quantum neural networks

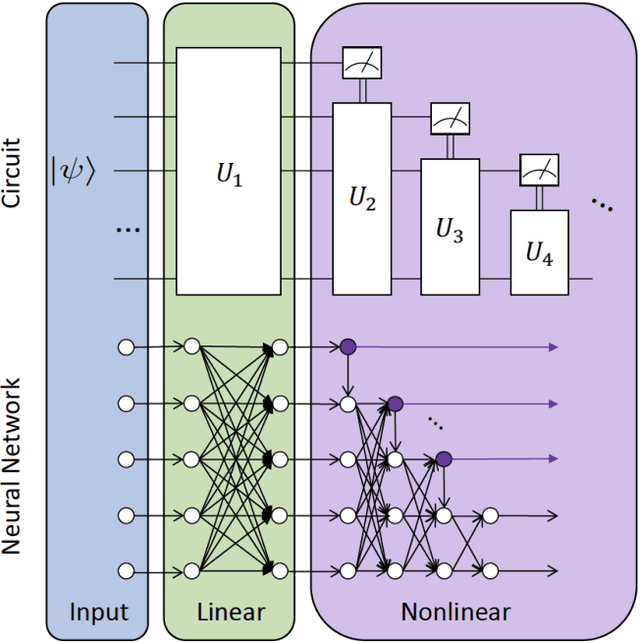
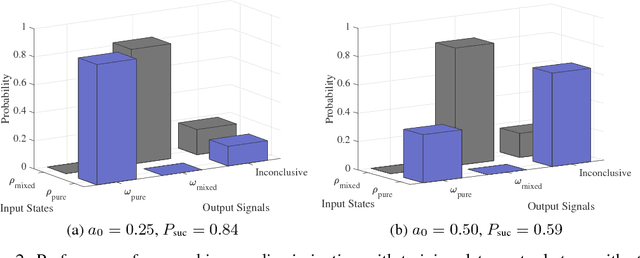
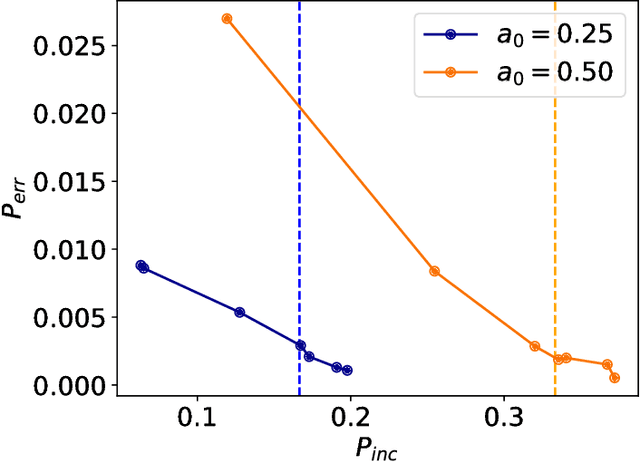
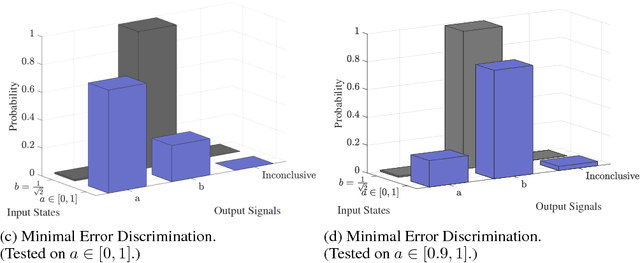
Quantum mechanics fundamentally forbids deterministic discrimination of quantum states and processes. However, the ability to optimally distinguish various classes of quantum data is an important primitive in quantum information science. In this work, we train near-term quantum circuits to classify data represented by non-orthogonal quantum probability distributions using the Adam stochastic optimization algorithm. This is achieved by iterative interactions of a classical device with a quantum processor to discover the parameters of an unknown non-unitary quantum circuit. This circuit learns to simulates the unknown structure of a generalized quantum measurement, or Positive-Operator-Value-Measure (POVM), that is required to optimally distinguish possible distributions of quantum inputs. Notably we use universal circuit topologies, with a theoretically motivated circuit design, which guarantees that our circuits can in principle learn to perform arbitrary input-output mappings. Our numerical simulations show that shallow quantum circuits could be trained to discriminate among various pure and mixed quantum states exhibiting a trade-off between minimizing erroneous and inconclusive outcomes with comparable performance to theoretically optimal POVMs. We train the circuit on different classes of quantum data and evaluate the generalization error on unseen mixed quantum states. This generalization power hence distinguishes our work from standard circuit optimization and provides an example of quantum machine learning for a task that has inherently no classical analogue.

Barren plateaus in quantum neural network training landscapes

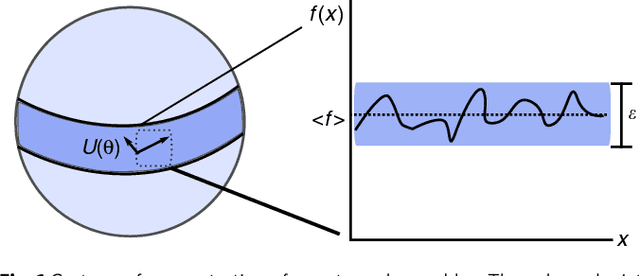
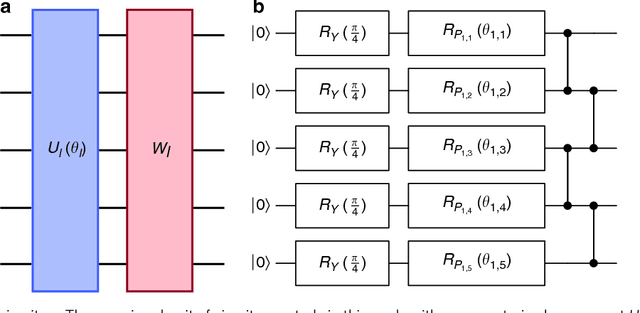
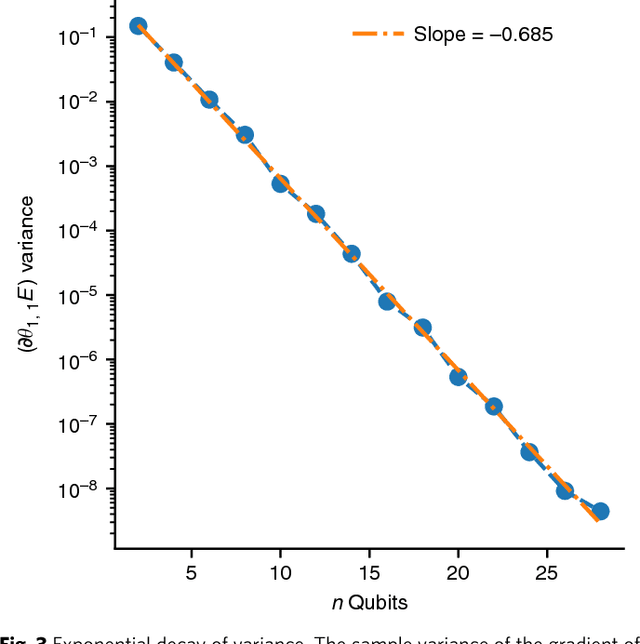
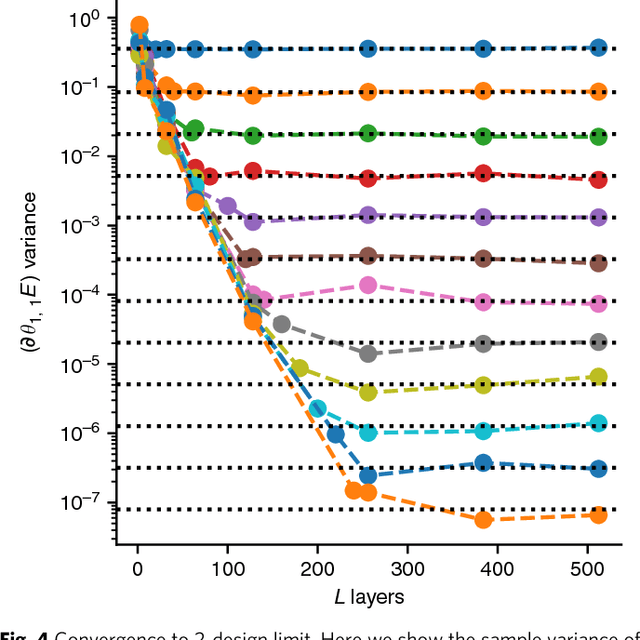
Many experimental proposals for noisy intermediate scale quantum devices involve training a parameterized quantum circuit with a classical optimization loop. Such hybrid quantum-classical algorithms are popular for applications in quantum simulation, optimization, and machine learning. Due to its simplicity and hardware efficiency, random circuits are often proposed as initial guesses for exploring the space of quantum states. We show that the exponential dimension of Hilbert space and the gradient estimation complexity make this choice unsuitable for hybrid quantum-classical algorithms run on more than a few qubits. Specifically, we show that for a wide class of reasonable parameterized quantum circuits, the probability that the gradient along any reasonable direction is non-zero to some fixed precision is exponentially small as a function of the number of qubits. We argue that this is related to the 2-design characteristic of random circuits, and that solutions to this problem must be studied.

Probabilistic Label Relation Graphs with Ising Models

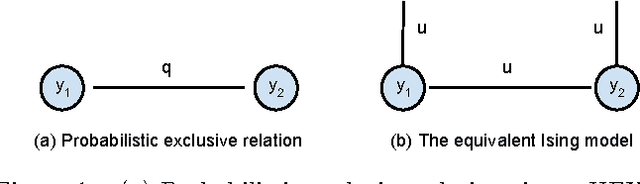
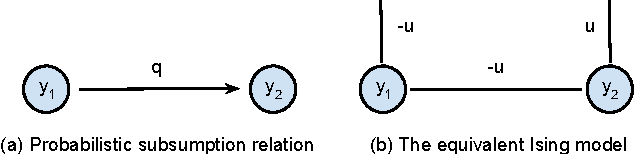
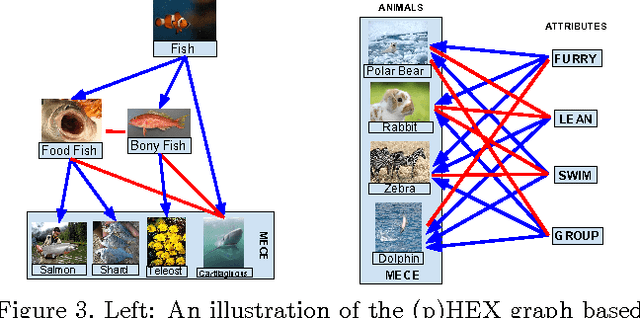
We consider classification problems in which the label space has structure. A common example is hierarchical label spaces, corresponding to the case where one label subsumes another (e.g., animal subsumes dog). But labels can also be mutually exclusive (e.g., dog vs cat) or unrelated (e.g., furry, carnivore). To jointly model hierarchy and exclusion relations, the notion of a HEX (hierarchy and exclusion) graph was introduced in [7]. This combined a conditional random field (CRF) with a deep neural network (DNN), resulting in state of the art results when applied to visual object classification problems where the training labels were drawn from different levels of the ImageNet hierarchy (e.g., an image might be labeled with the basic level category "dog", rather than the more specific label "husky"). In this paper, we extend the HEX model to allow for soft or probabilistic relations between labels, which is useful when there is uncertainty about the relationship between two labels (e.g., an antelope is "sort of" furry, but not to the same degree as a grizzly bear). We call our new model pHEX, for probabilistic HEX. We show that the pHEX graph can be converted to an Ising model, which allows us to use existing off-the-shelf inference methods (in contrast to the HEX method, which needed specialized inference algorithms). Experimental results show significant improvements in a number of large-scale visual object classification tasks, outperforming the previous HEX model.

Totally Corrective Boosting with Cardinality Penalization

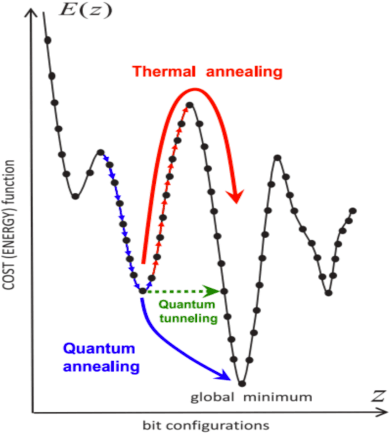
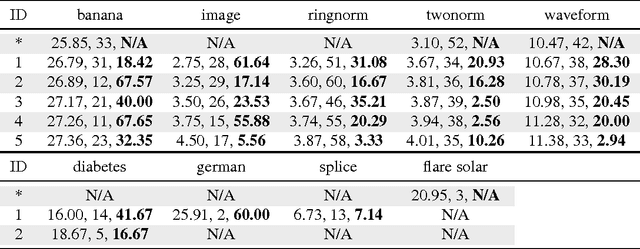
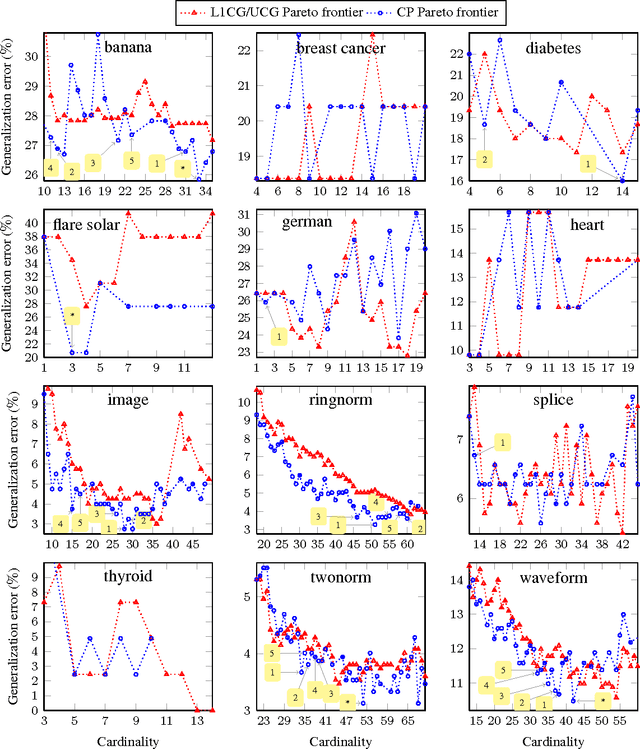
We propose a totally corrective boosting algorithm with explicit cardinality regularization. The resulting combinatorial optimization problems are not known to be efficiently solvable with existing classical methods, but emerging quantum optimization technology gives hope for achieving sparser models in practice. In order to demonstrate the utility of our algorithm, we use a distributed classical heuristic optimizer as a stand-in for quantum hardware. Even though this evaluation methodology incurs large time and resource costs on classical computing machinery, it allows us to gauge the potential gains in generalization performance and sparsity of the resulting boosted ensembles. Our experimental results on public data sets commonly used for benchmarking of boosting algorithms decidedly demonstrate the existence of such advantages. If actual quantum optimization were to be used with this algorithm in the future, we would expect equivalent or superior results at much smaller time and energy costs during training. Moreover, studying cardinality-penalized boosting also sheds light on why unregularized boosting algorithms with early stopping often yield better results than their counterparts with explicit convex regularization: Early stopping performs suboptimal cardinality regularization. The results that we present here indicate it is beneficial to explicitly solve the combinatorial problem still left open at early termination.

Construction of non-convex polynomial loss functions for training a binary classifier with quantum annealing

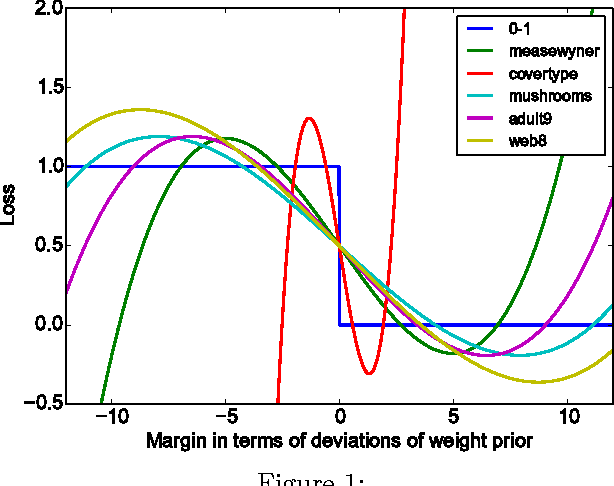
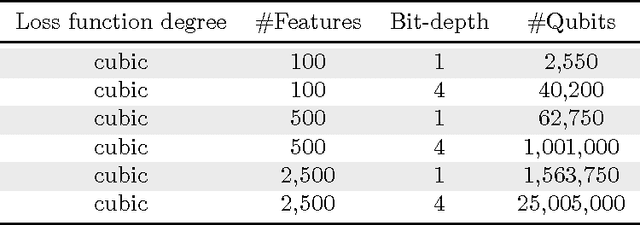
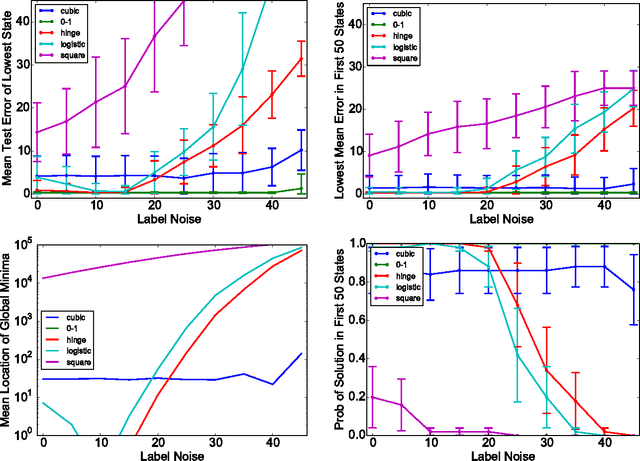
Quantum annealing is a heuristic quantum algorithm which exploits quantum resources to minimize an objective function embedded as the energy levels of a programmable physical system. To take advantage of a potential quantum advantage, one needs to be able to map the problem of interest to the native hardware with reasonably low overhead. Because experimental considerations constrain our objective function to take the form of a low degree PUBO (polynomial unconstrained binary optimization), we employ non-convex loss functions which are polynomial functions of the margin. We show that these loss functions are robust to label noise and provide a clear advantage over convex methods. These loss functions may also be useful for classical approaches as they compile to regularized risk expressions which can be evaluated in constant time with respect to the number of training examples.

Training a Large Scale Classifier with the Quantum Adiabatic Algorithm

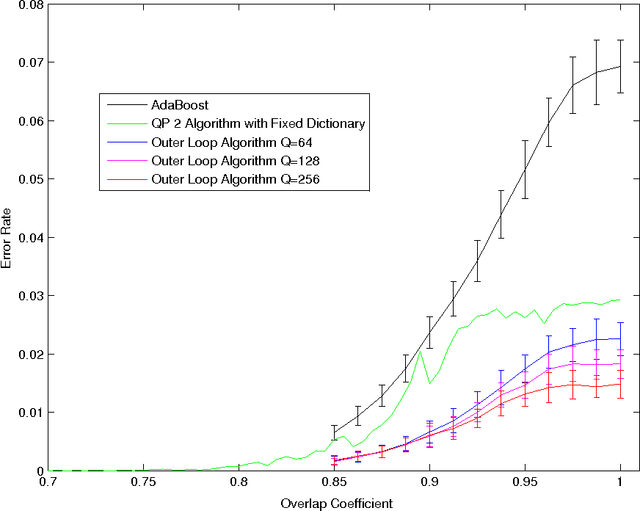
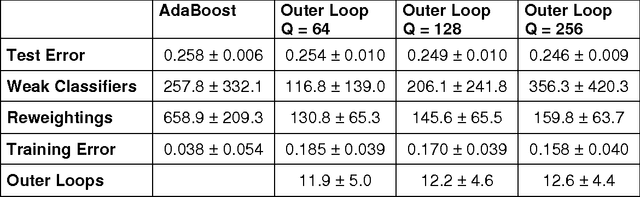
In a previous publication we proposed discrete global optimization as a method to train a strong binary classifier constructed as a thresholded sum over weak classifiers. Our motivation was to cast the training of a classifier into a format amenable to solution by the quantum adiabatic algorithm. Applying adiabatic quantum computing (AQC) promises to yield solutions that are superior to those which can be achieved with classical heuristic solvers. Interestingly we found that by using heuristic solvers to obtain approximate solutions we could already gain an advantage over the standard method AdaBoost. In this communication we generalize the baseline method to large scale classifier training. By large scale we mean that either the cardinality of the dictionary of candidate weak classifiers or the number of weak learners used in the strong classifier exceed the number of variables that can be handled effectively in a single global optimization. For such situations we propose an iterative and piecewise approach in which a subset of weak classifiers is selected in each iteration via global optimization. The strong classifier is then constructed by concatenating the subsets of weak classifiers. We show in numerical studies that the generalized method again successfully competes with AdaBoost. We also provide theoretical arguments as to why the proposed optimization method, which does not only minimize the empirical loss but also adds L0-norm regularization, is superior to versions of boosting that only minimize the empirical loss. By conducting a Quantum Monte Carlo simulation we gather evidence that the quantum adiabatic algorithm is able to handle a generic training problem efficiently.