Best practices for machine learning in antibody discovery and development

Over the past 40 years, the discovery and development of therapeutic antibodies to treat disease has become common practice. However, as therapeutic antibody constructs are becoming more sophisticated (e.g., multi-specifics), conventional approaches to optimisation are increasingly inefficient. Machine learning (ML) promises to open up an in silico route to antibody discovery and help accelerate the development of drug products using a reduced number of experiments and hence cost. Over the past few years, we have observed rapid developments in the field of ML-guided antibody discovery and development (D&D). However, many of the results are difficult to compare or hard to assess for utility by other experts in the field due to the high diversity in the datasets and evaluation techniques and metrics that are across industry and academia. This limitation of the literature curtails the broad adoption of ML across the industry and slows down overall progress in the field, highlighting the need to develop standards and guidelines that may help improve the reproducibility of ML models across different research groups. To address these challenges, we set out in this perspective to critically review current practices, explain common pitfalls, and clearly define a set of method development and evaluation guidelines that can be applied to different types of ML-based techniques for therapeutic antibody D&D. Specifically, we address in an end-to-end analysis, challenges associated with all aspects of the ML process and recommend a set of best practices for each stage.

Quantum Machine Learning For Classical Data

In this dissertation, we study the intersection of quantum computing and supervised machine learning algorithms, which means that we investigate quantum algorithms for supervised machine learning that operate on classical data. This area of research falls under the umbrella of quantum machine learning, a research area of computer science which has recently received wide attention. In particular, we investigate to what extent quantum computers can be used to accelerate supervised machine learning algorithms. The aim of this is to develop a clear understanding of the promises and limitations of the current state of the art of quantum algorithms for supervised machine learning, but also to define directions for future research in this exciting field. We start by looking at supervised quantum machine learning (QML) algorithms through the lens of statistical learning theory. In this framework, we derive novel bounds on the computational complexities of a large set of supervised QML algorithms under the requirement of optimal learning rates. Next, we give a new bound for Hamiltonian simulation of dense Hamiltonians, a major subroutine of most known supervised QML algorithms, and then derive a classical algorithm with nearly the same complexity. We then draw the parallels to recent "quantum-inspired" results, and will explain the implications of these results for quantum machine learning applications. Looking for areas which might bear larger advantages for QML algorithms, we finally propose a novel algorithm for Quantum Boltzmann machines, and argue that quantum algorithms for quantum data are one of the most promising applications for QML with potentially exponential advantage over classical approaches.

Fast quantum learning with statistical guarantees

Within the framework of statistical learning theory it is possible to bound the minimum number of samples required by a learner to reach a target accuracy. We show that if the bound on the accuracy is taken into account, quantum machine learning algorithms -- for which statistical guarantees are available -- cannot achieve polylogarithmic runtimes in the input dimension. This calls for a careful revaluation of quantum speedups for learning problems, even in cases where quantum access to the data is naturally available.

Generative training of quantum Boltzmann machines with hidden units

In this article we provide a method for fully quantum generative training of quantum Boltzmann machines with both visible and hidden units while using quantum relative entropy as an objective. This is significant because prior methods were not able to do so due to mathematical challenges posed by the gradient evaluation. We present two novel methods for solving this problem. The first proposal addresses it, for a class of restricted quantum Boltzmann machines with mutually commuting Hamiltonians on the hidden units, by using a variational upper bound on the quantum relative entropy. The second one uses high-order divided difference methods and linear-combinations of unitaries to approximate the exact gradient of the relative entropy for a generic quantum Boltzmann machine. Both methods are efficient under the assumption that Gibbs state preparation is efficient and that the Hamiltonian are given by a sparse row-computable matrix.

Adversarial quantum circuit learning for pure state approximation

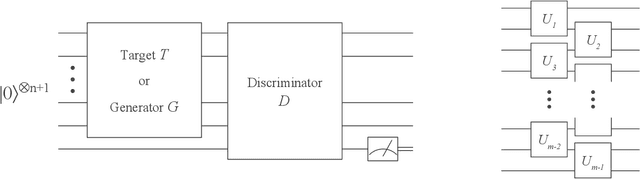
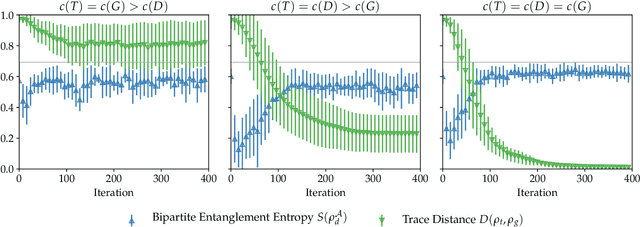
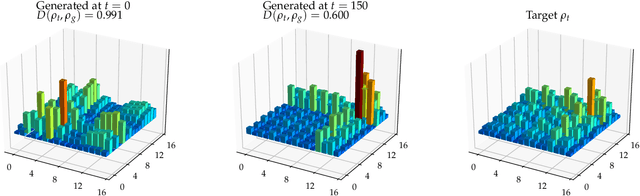
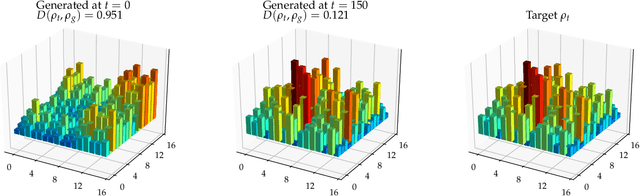
Adversarial learning is one of the most successful approaches to modelling high-dimensional probability distributions from data. The quantum computing community has recently begun to generalise this idea and to look for potential applications. In this work, we derive an adversarial algorithm for the problem of approximating an unknown quantum pure state. Although this could be done on universal quantum computers, the adversarial formulation enables us to execute the algorithm on near-term quantum computers. Two parametrized circuits are optimized in tandem: One tries to approximate the target state, the other tries to distinguish between target and approximated state. Supported by numerical simulations, we show that resilient backpropagation algorithms perform remarkably well in optimizing the two circuits. We use the bipartite entanglement entropy to design an efficient heuristic for the stopping criterion. Our approach may find application in quantum state tomography.

Approximating Hamiltonian dynamics with the Nyström method

Simulating the time-evolution of quantum mechanical systems is BQP-hard and expected to be one of the foremost applications of quantum computers. We consider the approximation of Hamiltonian dynamics using subsampling methods from randomized numerical linear algebra. We propose conditions for the efficient approximation of state vectors evolving under a given Hamiltonian. As an immediate application, we show that sample based quantum simulation, a type of evolution where the Hamiltonian is a density matrix, can be efficiently classically simulated under specific structural conditions. Our main technical contribution is a randomized algorithm for approximating Hermitian matrix exponentials. The proof leverages the Nystr\"om method to obtain low-rank approximations of the Hamiltonian. We envisage that techniques from randomized linear algebra will bring further insights into the power of quantum computation.

Universal discriminative quantum neural networks

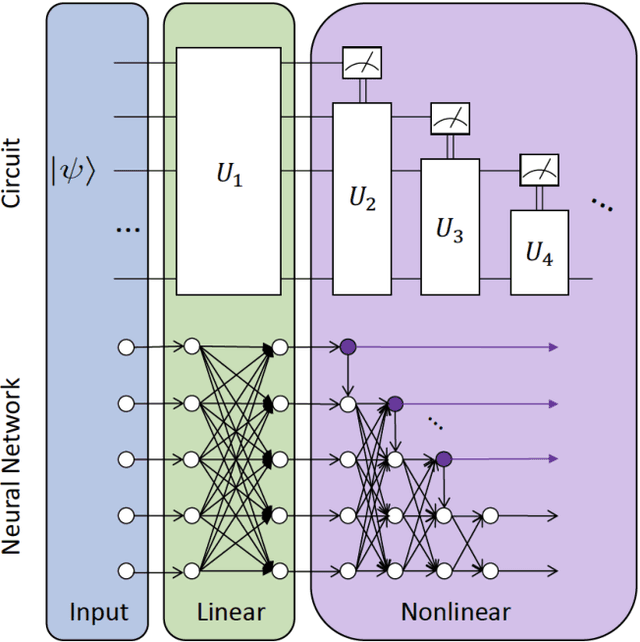
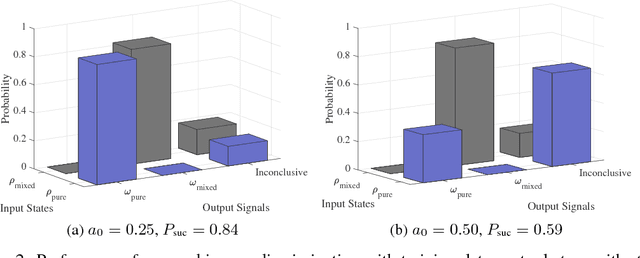
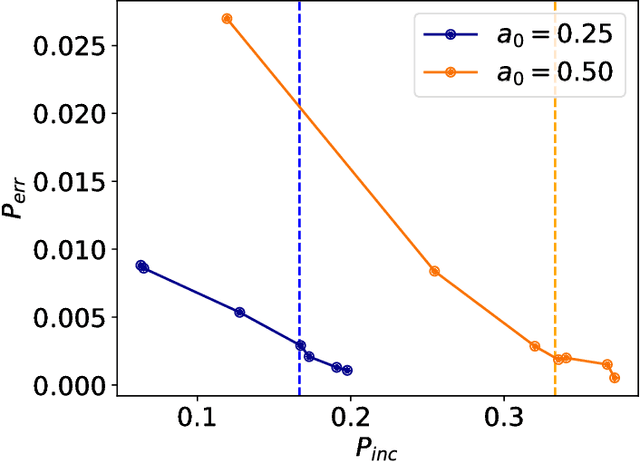
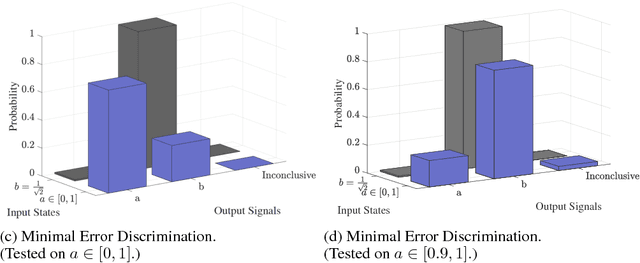
Quantum mechanics fundamentally forbids deterministic discrimination of quantum states and processes. However, the ability to optimally distinguish various classes of quantum data is an important primitive in quantum information science. In this work, we train near-term quantum circuits to classify data represented by non-orthogonal quantum probability distributions using the Adam stochastic optimization algorithm. This is achieved by iterative interactions of a classical device with a quantum processor to discover the parameters of an unknown non-unitary quantum circuit. This circuit learns to simulates the unknown structure of a generalized quantum measurement, or Positive-Operator-Value-Measure (POVM), that is required to optimally distinguish possible distributions of quantum inputs. Notably we use universal circuit topologies, with a theoretically motivated circuit design, which guarantees that our circuits can in principle learn to perform arbitrary input-output mappings. Our numerical simulations show that shallow quantum circuits could be trained to discriminate among various pure and mixed quantum states exhibiting a trade-off between minimizing erroneous and inconclusive outcomes with comparable performance to theoretically optimal POVMs. We train the circuit on different classes of quantum data and evaluate the generalization error on unseen mixed quantum states. This generalization power hence distinguishes our work from standard circuit optimization and provides an example of quantum machine learning for a task that has inherently no classical analogue.

Quantum machine learning: a classical perspective

Recently, increased computational power and data availability, as well as algorithmic advances, have led machine learning techniques to impressive results in regression, classification, data-generation and reinforcement learning tasks. Despite these successes, the proximity to the physical limits of chip fabrication alongside the increasing size of datasets are motivating a growing number of researchers to explore the possibility of harnessing the power of quantum computation to speed-up classical machine learning algorithms. Here we review the literature in quantum machine learning and discuss perspectives for a mixed readership of classical machine learning and quantum computation experts. Particular emphasis will be placed on clarifying the limitations of quantum algorithms, how they compare with their best classical counterparts and why quantum resources are expected to provide advantages for learning problems. Learning in the presence of noise and certain computationally hard problems in machine learning are identified as promising directions for the field. Practical questions, like how to upload classical data into quantum form, will also be addressed.