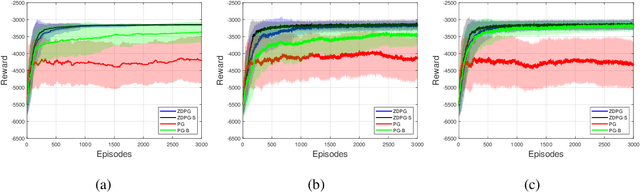
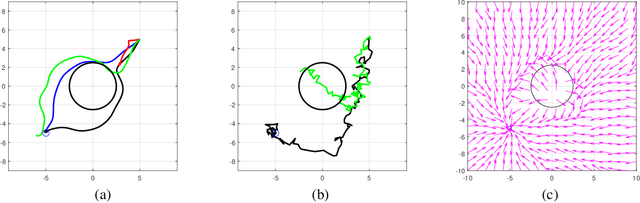
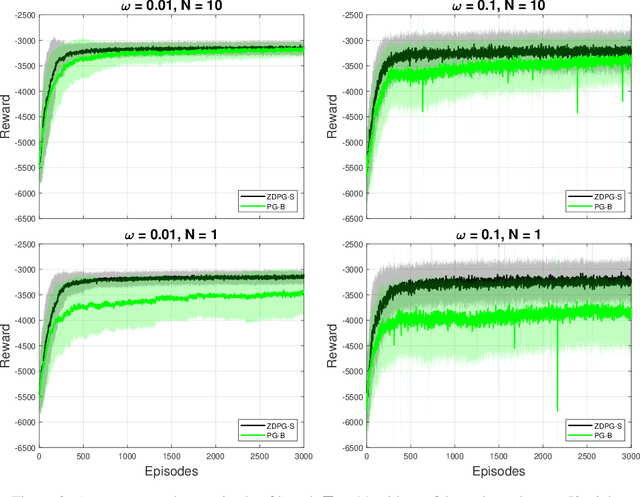
Zeroth-order Deterministic Policy Gradient

Deterministic Policy Gradient (DPG) removes a level of randomness from standard randomized-action Policy Gradient (PG), and demonstrates substantial empirical success for tackling complex dynamic problems involving Markov decision processes. At the same time, though, DPG loses its ability to learn in a model-free (i.e., actor-only) fashion, frequently necessitating the use of critics in order to obtain consistent estimates of the associated policy-reward gradient. In this work, we introduce Zeroth-order Deterministic Policy Gradient (ZDPG), which approximates policy-reward gradients via two-point stochastic evaluations of the $Q$-function, constructed by properly designed low-dimensional action-space perturbations. Exploiting the idea of random horizon rollouts for obtaining unbiased estimates of the $Q$-function, ZDPG lifts the dependence on critics and restores true model-free policy learning, while enjoying built-in and provable algorithmic stability. Additionally, we present new finite sample complexity bounds for ZDPG, which improve upon existing results by up to two orders of magnitude. Our findings are supported by several numerical experiments, which showcase the effectiveness of ZDPG in a practical setting, and its advantages over both PG and Baseline PG.

Learning to Track Dynamic Targets in Partially Known Environments

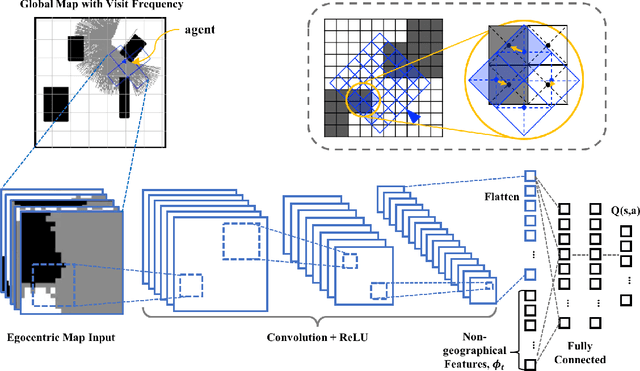
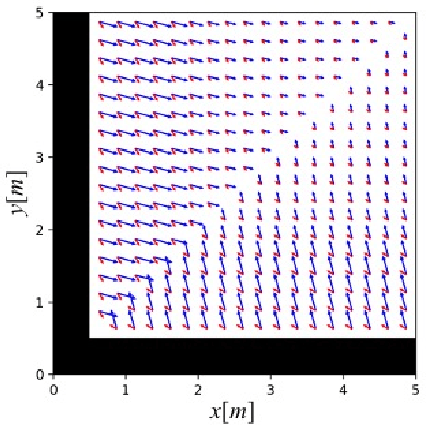
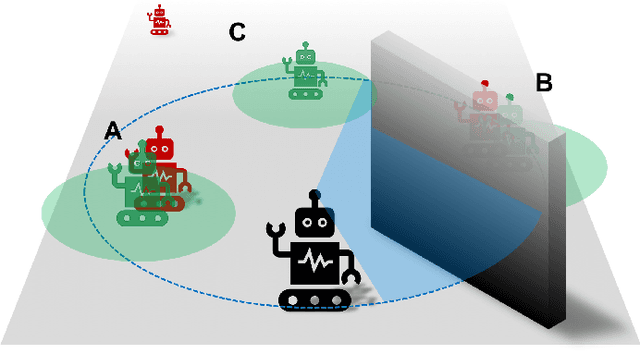
We solve active target tracking, one of the essential tasks in autonomous systems, using a deep reinforcement learning (RL) approach. In this problem, an autonomous agent is tasked with acquiring information about targets of interests using its onboard sensors. The classical challenges in this problem are system model dependence and the difficulty of computing information-theoretic cost functions for a long planning horizon. RL provides solutions for these challenges as the length of its effective planning horizon does not affect the computational complexity, and it drops the strong dependency of an algorithm on system models. In particular, we introduce Active Tracking Target Network (ATTN), a unified RL policy that is capable of solving major sub-tasks of active target tracking -- in-sight tracking, navigation, and exploration. The policy shows robust behavior for tracking agile and anomalous targets with a partially known target model. Additionally, the same policy is able to navigate in obstacle environments to reach distant targets as well as explore the environment when targets are positioned in unexpected locations.

Model-Based Robust Deep Learning

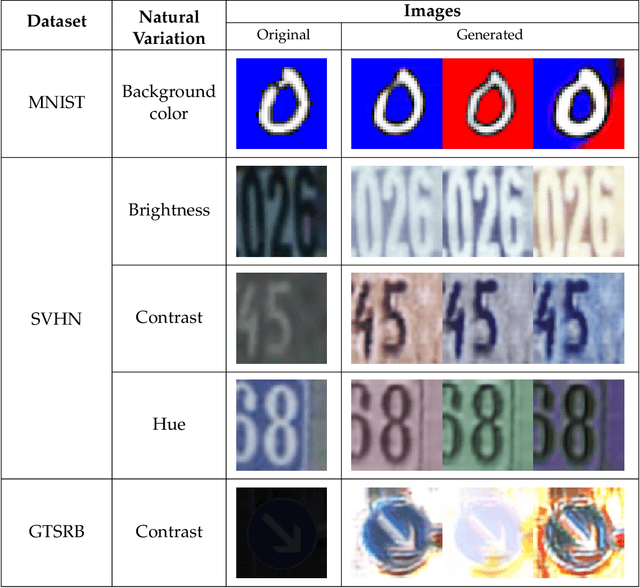
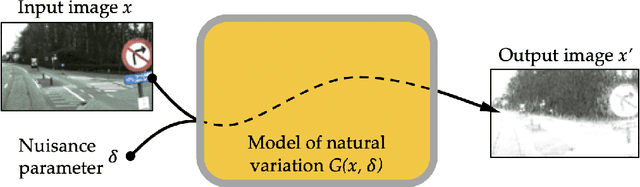
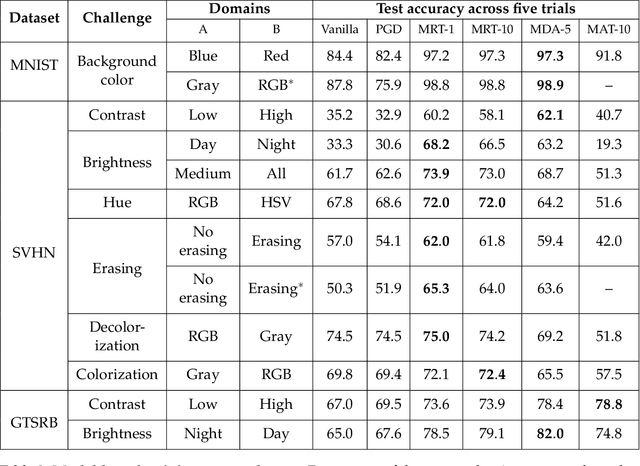
While deep learning has resulted in major breakthroughs in many application domains, the frameworks commonly used in deep learning remain fragile to artificially-crafted and imperceptible changes in the data. In response to this fragility, adversarial training has emerged as a principled approach for enhancing the robustness of deep learning with respect to norm-bounded perturbations. However, there are other sources of fragility for deep learning that are arguably more common and less thoroughly studied. Indeed, natural variation such as lighting or weather conditions can significantly degrade the accuracy of trained neural networks, proving that such natural variation presents a significant challenge for deep learning. In this paper, we propose a paradigm shift from perturbation-based adversarial robustness toward {\em model-based robust deep learning}. Our objective is to provide general training algorithms that can be used to train deep neural networks to be robust against natural variation in data. Critical to our paradigm is first obtaining a \emph{model of natural variation} which can be used to vary data over a range of natural conditions. Such models may be either known a priori or else learned from data. In the latter case, we show that deep generative models can be used to learn models of natural variation that are consistent with realistic conditions. We then exploit such models in three novel model-based robust training algorithms in order to enhance the robustness of deep learning with respect to the given model. Our extensive experiments show that across a variety of naturally-occurring conditions and across various datasets, deep neural networks trained with our model-based algorithms significantly outperform both standard deep learning algorithms as well as norm-bounded robust deep learning algorithms.

Teaching Recurrent Neural Networks to Modify Chaotic Memories by Example

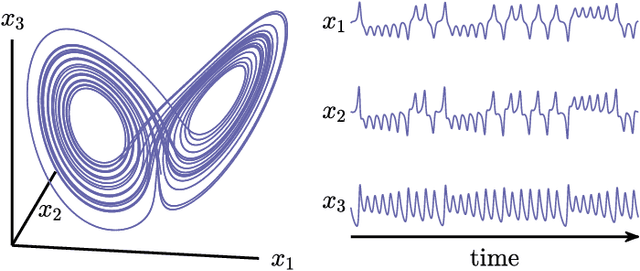
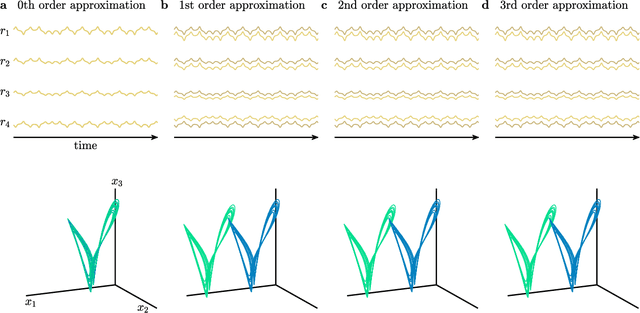
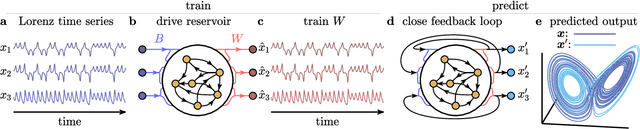
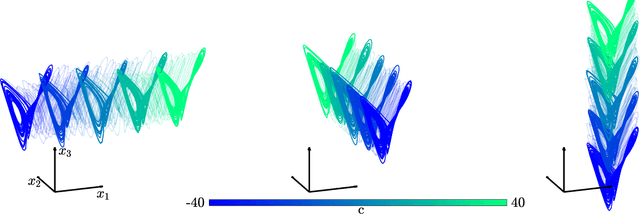
The ability to store and manipulate information is a hallmark of computational systems. Whereas computers are carefully engineered to represent and perform mathematical operations on structured data, neurobiological systems perform analogous functions despite flexible organization and unstructured sensory input. Recent efforts have made progress in modeling the representation and recall of information in neural systems. However, precisely how neural systems learn to modify these representations remains far from understood. Here we demonstrate that a recurrent neural network (RNN) can learn to modify its representation of complex information using only examples, and we explain the associated learning mechanism with new theory. Specifically, we drive an RNN with examples of translated, linearly transformed, or pre-bifurcated time series from a chaotic Lorenz system, alongside an additional control signal that changes value for each example. By training the network to replicate the Lorenz inputs, it learns to autonomously evolve about a Lorenz-shaped manifold. Additionally, it learns to continuously interpolate and extrapolate the translation, transformation, and bifurcation of this representation far beyond the training data by changing the control signal. Finally, we provide a mechanism for how these computations are learned, and demonstrate that a single network can simultaneously learn multiple computations. Together, our results provide a simple but powerful mechanism by which an RNN can learn to manipulate internal representations of complex information, allowing for the principled study and precise design of RNNs.

Robust Deep Learning as Optimal Control: Insights and Convergence Guarantees

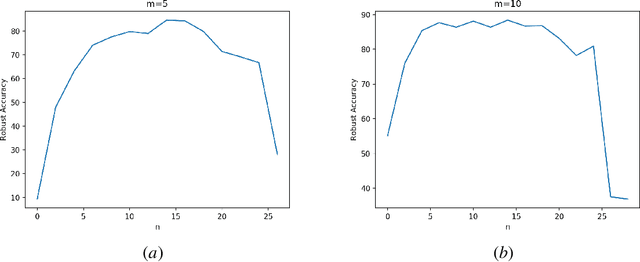
The fragility of deep neural networks to adversarially-chosen inputs has motivated the need to revisit deep learning algorithms. Including adversarial examples during training is a popular defense mechanism against adversarial attacks. This mechanism can be formulated as a min-max optimization problem, where the adversary seeks to maximize the loss function using an iterative first-order algorithm while the learner attempts to minimize it. However, finding adversarial examples in this way causes excessive computational overhead during training. By interpreting the min-max problem as an optimal control problem, it has recently been shown that one can exploit the compositional structure of neural networks in the optimization problem to improve the training time significantly. In this paper, we provide the first convergence analysis of this adversarial training algorithm by combining techniques from robust optimal control and inexact oracle methods in optimization. Our analysis sheds light on how the hyperparameters of the algorithm affect the its stability and convergence. We support our insights with experiments on a robust classification problem.

Reach-SDP: Reachability Analysis of Closed-Loop Systems with Neural Network Controllers via Semidefinite Programming

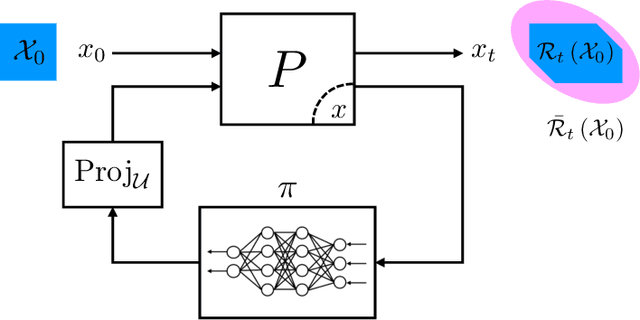
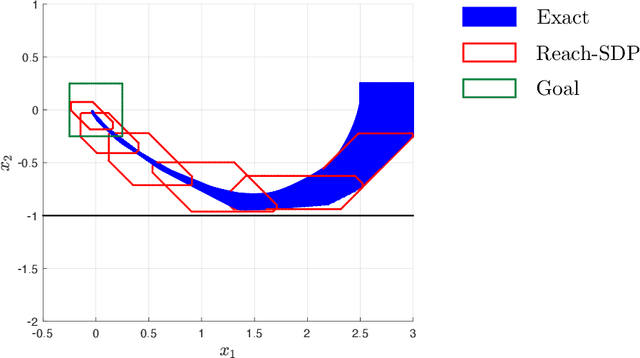
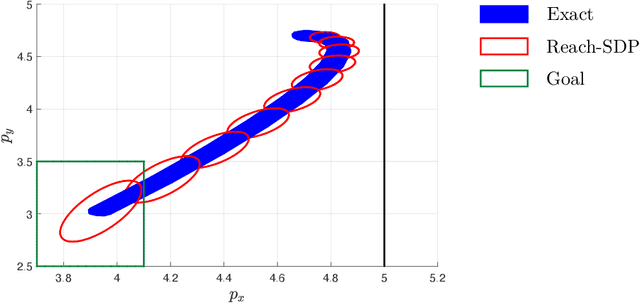
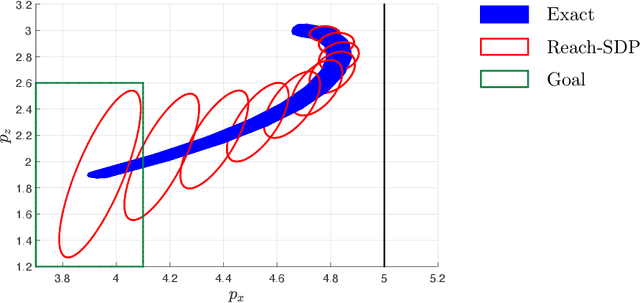
There has been an increasing interest in using neural networks in closed-loop control systems to improve performance and reduce computational costs for on-line implementation. However, providing safety and stability guarantees for these systems is challenging due to the nonlinear and compositional structure of neural networks. In this paper, we propose a novel forward reachability analysis method for the safety verification of linear time-varying systems with neural networks in feedback interconnection. Our technical approach relies on abstracting the nonlinear activation functions by quadratic constraints, which leads to an outer-approximation of forward reachable sets of the closed-loop system. We show that we can compute these approximate reachable sets using semidefinite programming. We illustrate our method in a quadrotor example, in which we first approximate a nonlinear model predictive controller via a deep neural network and then apply our analysis tool to certify finite-time reachability and constraint satisfaction of the closed-loop system.

Technical Report: Reactive Semantic Planning in Unexplored Semantic Environments Using Deep Perceptual Feedback

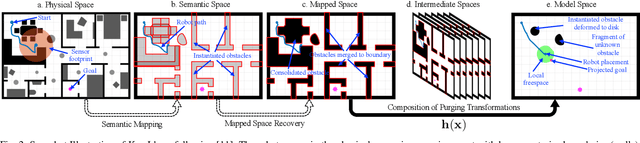
This paper presents a reactive planning system that enriches the topological representation of an environment with a tightly integrated semantic representation, achieved by incorporating and exploiting advances in deep perceptual learning and probabilistic semantic reasoning. Our architecture combines object detection with semantic SLAM, affording robust, reactive logical as well as geometric planning in unexplored environments. Moreover, by incorporating a human mesh estimation algorithm, our system is capable of reacting and responding in real time to semantically labeled human motions and gestures. New formal results allow tracking of suitably non-adversarial moving targets, while maintaining the same collision avoidance guarantees. We suggest the empirical utility of the proposed control architecture with a numerical study including comparisons with a state-of-the-art dynamic replanning algorithm, and physical implementation on both a wheeled and legged platform in different settings with both geometric and semantic goals.

Sample Complexity of Kalman Filtering for Unknown Systems

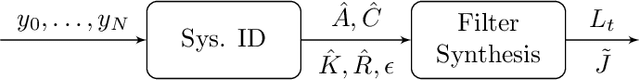
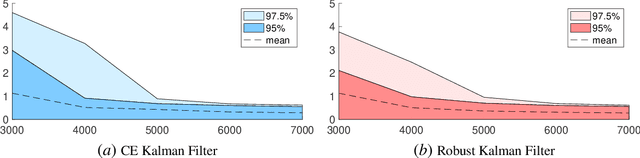
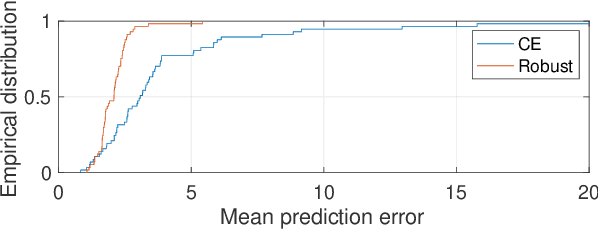
In this paper, we consider the task of designing a Kalman Filter (KF) for an unknown and partially observed autonomous linear time invariant system driven by process and sensor noise. To do so, we propose studying the following two step process: first, using system identification tools rooted in subspace methods, we obtain coarse finite-data estimates of the state-space parameters and Kalman gain describing the autonomous system; and second, we use these approximate parameters to design a filter which produces estimates of the system state. We show that when the system identification step produces sufficiently accurate estimates, or when the underlying true KF is sufficiently robust, that a Certainty Equivalent (CE) KF, i.e., one designed using the estimated parameters directly, enjoys provable sub-optimality guarantees. We further show that when these conditions fail, and in particular, when the CE KF is marginally stable (i.e., has eigenvalues very close to the unit circle), that imposing additional robustness constraints on the filter leads to similar sub-optimality guarantees. We further show that with high probability, both the CE and robust filters have mean prediction error bounded by $\tilde O(1/\sqrt{N})$, where $N$ is the number of data points collected in the system identification step. To the best of our knowledge, these are the first end-to-end sample complexity bounds for the Kalman Filtering of an unknown system.

Risk-Aware MMSE Estimation

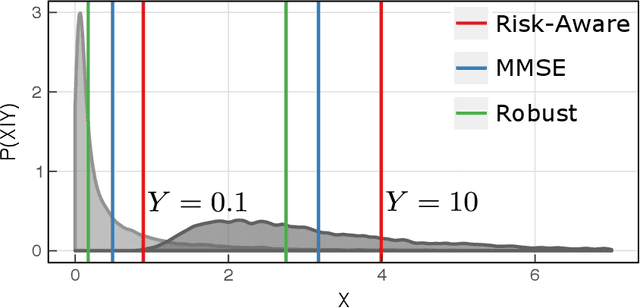
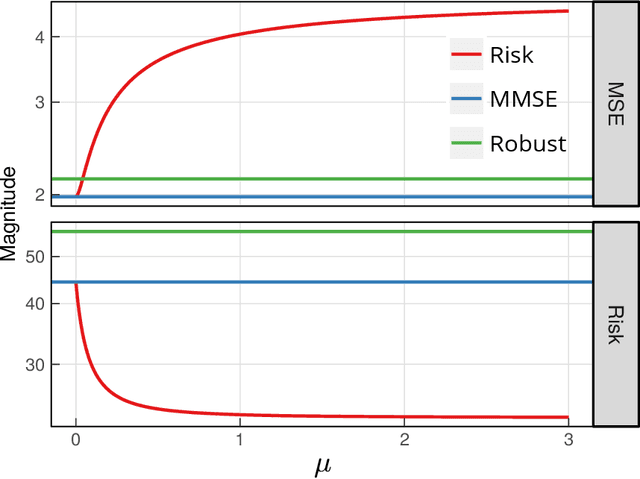
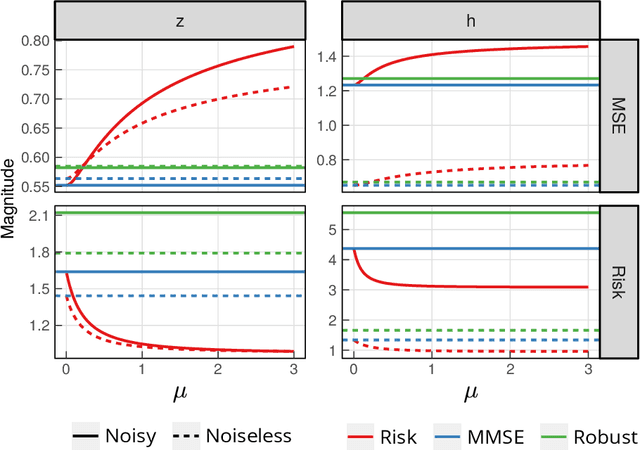
Despite the simplicity and intuitive interpretation of Minimum Mean Squared Error (MMSE) estimators, their effectiveness in certain scenarios is questionable. Indeed, minimizing squared errors on average does not provide any form of stability, as the volatility of the estimation error is left unconstrained. When this volatility is statistically significant, the difference between the average and realized performance of the MMSE estimator can be drastically different. To address this issue, we introduce a new risk-aware MMSE formulation which trades between mean performance and risk by explicitly constraining the expected predictive variance of the involved squared error. We show that, under mild moment boundedness conditions, the corresponding risk-aware optimal solution can be evaluated explicitly, and has the form of an appropriately biased nonlinear MMSE estimator. We further illustrate the effectiveness of our approach via several numerical examples, which also showcase the advantages of risk-aware MMSE estimation against risk-neutral MMSE estimation, especially in models involving skewed, heavy-tailed distributions.

Model-Free Learning of Optimal Ergodic Policies in Wireless Systems

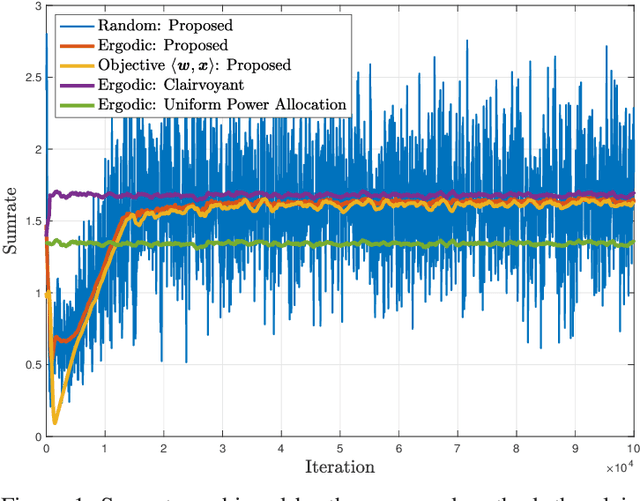
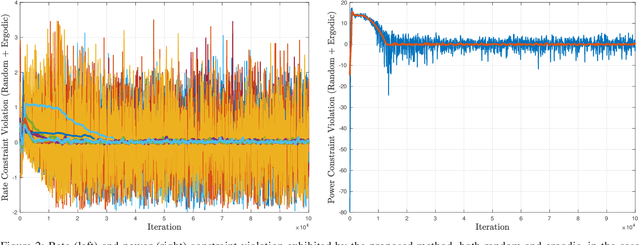
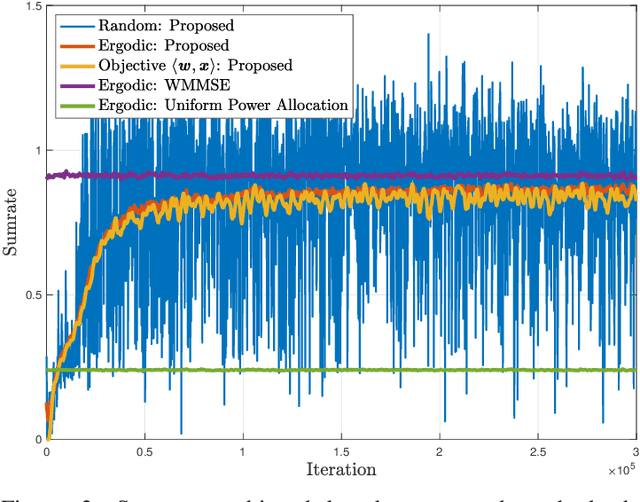
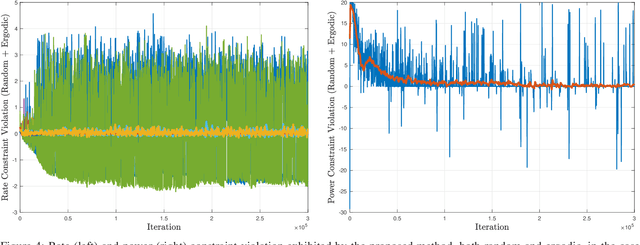
Learning optimal resource allocation policies in wireless systems can be effectively achieved by formulating finite dimensional constrained programs which depend on system configuration, as well as the adopted learning parameterization. The interest here is in cases where system models are unavailable, prompting methods that probe the wireless system with candidate policies, and then use observed performance to determine better policies. This generic procedure is difficult because of the need to cull accurate gradient estimates out of these limited system queries. This paper constructs and exploits smoothed surrogates of constrained ergodic resource allocation problems, the gradients of the former being representable exactly as averages of finite differences that can be obtained through limited system probing. Leveraging this unique property, we develop a new model-free primal-dual algorithm for learning optimal ergodic resource allocations, while we rigorously analyze the relationships between original policy search problems and their surrogates, in both primal and dual domains. First, we show that both primal and dual domain surrogates are uniformly consistent approximations of their corresponding original finite dimensional counterparts. Upon further assuming the use of near-universal policy parameterizations, we also develop explicit bounds on the gap between optimal values of initial, infinite dimensional resource allocation problems, and dual values of their parameterized smoothed surrogates. In fact, we show that this duality gap decreases at a linear rate relative to smoothing and universality parameters. Thus, it can be made arbitrarily small at will, also justifying our proposed primal-dual algorithmic recipe. Numerical simulations confirm the effectiveness of our approach.