Autonomous Blimp Control using Deep Reinforcement Learning

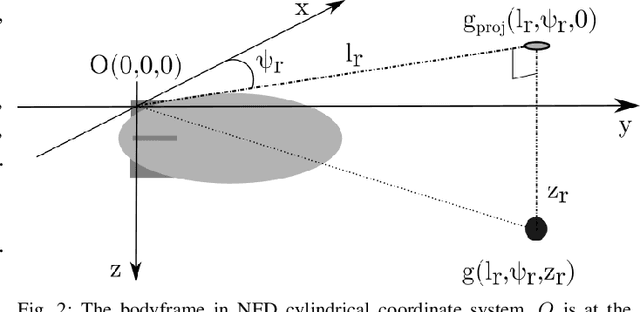
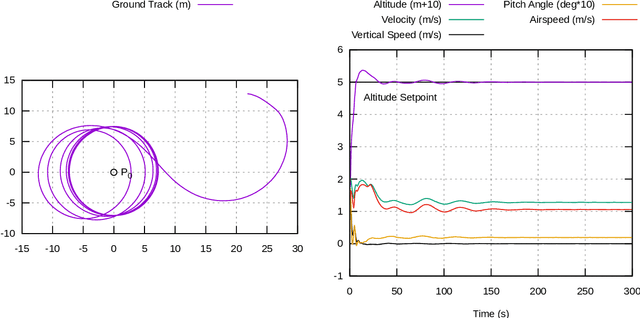
Aerial robot solutions are becoming ubiquitous for an increasing number of tasks. Among the various types of aerial robots, blimps are very well suited to perform long-duration tasks while being energy efficient, relatively silent and safe. To address the blimp navigation and control task, in our recent work, we have developed a software-in-the-loop simulation and a PID-based controller for large blimps in the presence of wind disturbance. However, blimps have a deformable structure and their dynamics are inherently non-linear and time-delayed, often resulting in large trajectory tracking errors. Moreover, the buoyancy of a blimp is constantly changing due to changes in the ambient temperature and pressure. In the present paper, we explore a deep reinforcement learning (DRL) approach to address these issues. We train only in simulation, while keeping conditions as close as possible to the real-world scenario. We derive a compact state representation to reduce the training time and a discrete action space to enforce control smoothness. Our initial results in simulation show a significant potential of DRL in solving the blimp control task and robustness against moderate wind and parameter uncertainty. Extensive experiments are presented to study the robustness of our approach. We also openly provide the source code of our approach.

Robust Compressed Sensing MRI with Deep Generative Priors

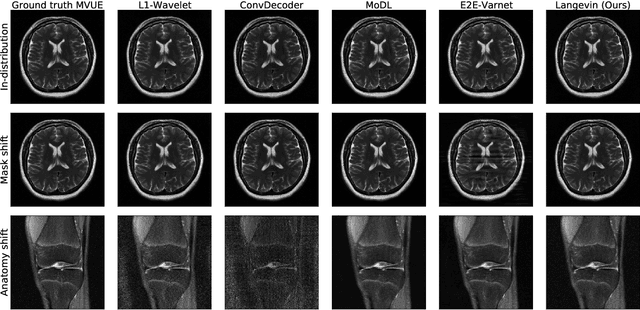
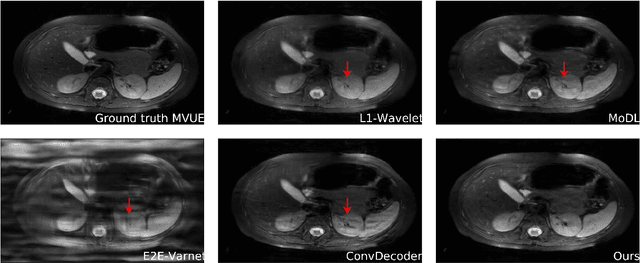
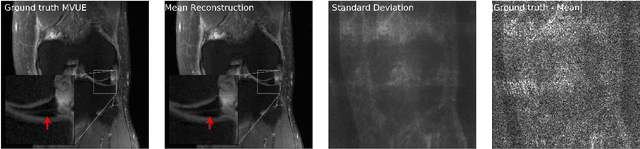
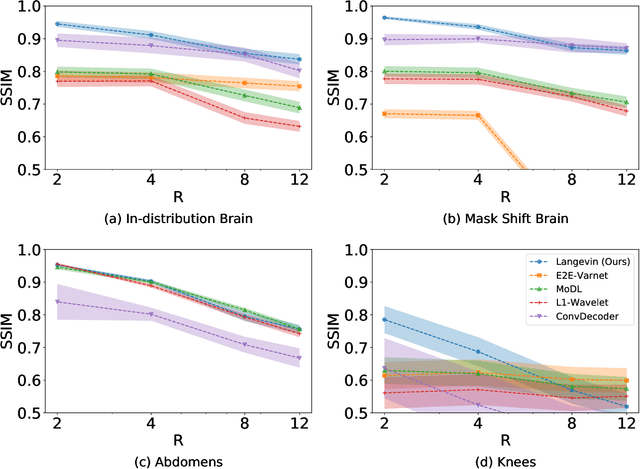
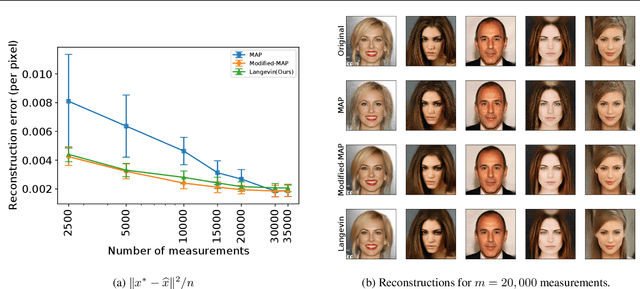
The CSGM framework (Bora-Jalal-Price-Dimakis'17) has shown that deep generative priors can be powerful tools for solving inverse problems. However, to date this framework has been empirically successful only on certain datasets (for example, human faces and MNIST digits), and it is known to perform poorly on out-of-distribution samples. In this paper, we present the first successful application of the CSGM framework on clinical MRI data. We train a generative prior on brain scans from the fastMRI dataset, and show that posterior sampling via Langevin dynamics achieves high quality reconstructions. Furthermore, our experiments and theory show that posterior sampling is robust to changes in the ground-truth distribution and measurement process. Our code and models are available at: \url{https://github.com/utcsilab/csgm-mri-langevin}.

Fairness for Image Generation with Uncertain Sensitive Attributes

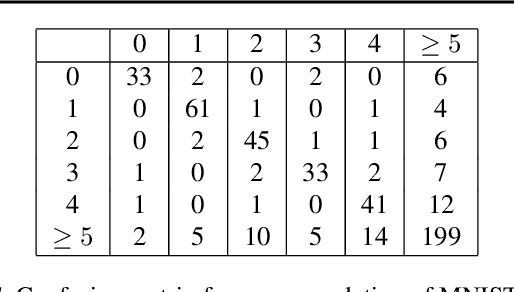
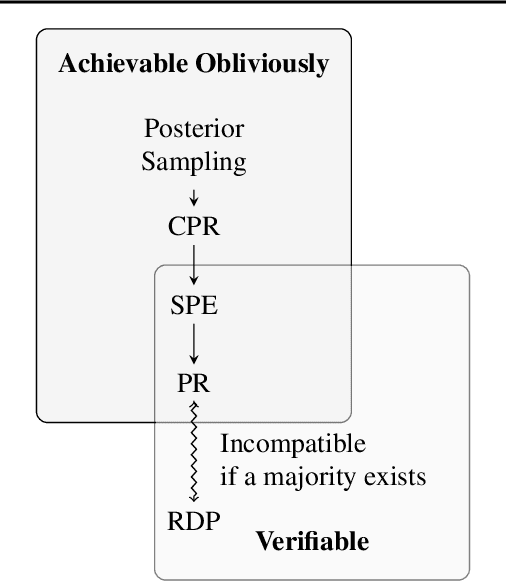
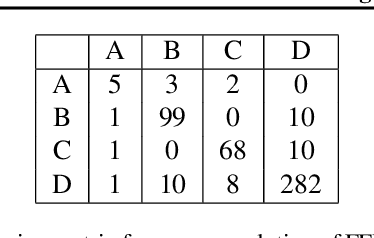
This work tackles the issue of fairness in the context of generative procedures, such as image super-resolution, which entail different definitions from the standard classification setting. Moreover, while traditional group fairness definitions are typically defined with respect to specified protected groups -- camouflaging the fact that these groupings are artificial and carry historical and political motivations -- we emphasize that there are no ground truth identities. For instance, should South and East Asians be viewed as a single group or separate groups? Should we consider one race as a whole or further split by gender? Choosing which groups are valid and who belongs in them is an impossible dilemma and being "fair" with respect to Asians may require being "unfair" with respect to South Asians. This motivates the introduction of definitions that allow algorithms to be \emph{oblivious} to the relevant groupings. We define several intuitive notions of group fairness and study their incompatibilities and trade-offs. We show that the natural extension of demographic parity is strongly dependent on the grouping, and \emph{impossible} to achieve obliviously. On the other hand, the conceptually new definition we introduce, Conditional Proportional Representation, can be achieved obliviously through Posterior Sampling. Our experiments validate our theoretical results and achieve fair image reconstruction using state-of-the-art generative models.

Instance-Optimal Compressed Sensing via Posterior Sampling

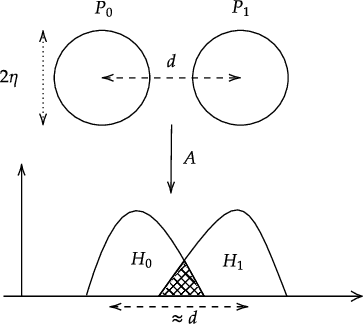
We characterize the measurement complexity of compressed sensing of signals drawn from a known prior distribution, even when the support of the prior is the entire space (rather than, say, sparse vectors). We show for Gaussian measurements and \emph{any} prior distribution on the signal, that the posterior sampling estimator achieves near-optimal recovery guarantees. Moreover, this result is robust to model mismatch, as long as the distribution estimate (e.g., from an invertible generative model) is close to the true distribution in Wasserstein distance. We implement the posterior sampling estimator for deep generative priors using Langevin dynamics, and empirically find that it produces accurate estimates with more diversity than MAP.

L1 Regression with Lewis Weights Subsampling

We consider the problem of finding an approximate solution to $\ell_1$ regression while only observing a small number of labels. Given an $n \times d$ unlabeled data matrix $X$, we must choose a small set of $m \ll n$ rows to observe the labels of, then output an estimate $\widehat{\beta}$ whose error on the original problem is within a $1 + \varepsilon$ factor of optimal. We show that sampling from $X$ according to its Lewis weights and outputting the empirical minimizer succeeds with probability $1-\delta$ for $m > O(\frac{1}{\varepsilon^2} d \log \frac{d}{\varepsilon \delta})$. This is analogous to the performance of sampling according to leverage scores for $\ell_2$ regression, but with exponentially better dependence on $\delta$. We also give a corresponding lower bound of $\Omega(\frac{d}{\varepsilon^2} + (d + \frac{1}{\varepsilon^2}) \log\frac{1}{\delta})$.

Linear Bandit Algorithms with Sublinear Time Complexity

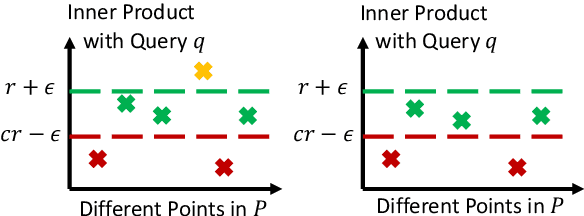
We propose to accelerate existing linear bandit algorithms to achieve per-step time complexity sublinear in the number of arms $K$. The key to sublinear complexity is the realization that the arm selection in many linear bandit algorithms reduces to the maximum inner product search (MIPS) problem. Correspondingly, we propose an algorithm that approximately solves the MIPS problem for a sequence of adaptive queries yielding near-linear preprocessing time complexity and sublinear query time complexity. Using the proposed MIPS solver as a sub-routine, we present two bandit algorithms (one based on UCB, and the other based on TS) that achieve sublinear time complexity. We explicitly characterize the tradeoff between the per-step time complexity and regret, and show that our proposed algorithms can achieve $O(K^{1-\alpha(T)})$ per-step complexity for some $\alpha(T) > 0$ and $\widetilde O(\sqrt{T})$ regret, where $T$ is the time horizon. Further, we present the theoretical limit of the tradeoff, which provides a lower bound for the per-step time complexity. We also discuss other choices of approximate MIPS algorithms and other applications to linear bandit problems.

Simulation and Control of Deformable Autonomous Airships in Turbulent Wind

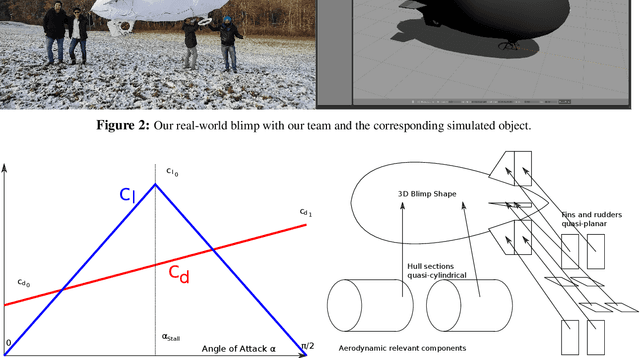
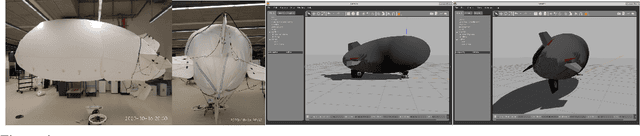
Abstract. Fixed wing and multirotor UAVs are common in the field of robotics. Solutions for simulation and control of these vehicles are ubiquitous. This is not the case for airships, a simulation of which needs to address unique properties, i) dynamic deformation in response to aerodynamic and control forces, ii) high susceptibility to wind and turbulence at low airspeed, iii) high variability in airship designs regarding placement, direction and vectoring of thrusters and control surfaces. We present a flexible framework for modeling, simulation and control of airships, based on the Robot operating system (ROS), simulation environment (Gazebo) and commercial off the shelf (COTS) electronics, both of which are open source. Based on simulated wind and deformation, we predict substantial effects on controllability, verified in real world flight experiments. All our code is shared as open source, for the benefit of the community and to facilitate lighter-than-air vehicle (LTAV) research. https://github.com/robot-perception-group/airship_simulation

Near-Optimal Learning of Tree-Structured Distributions by Chow-Liu

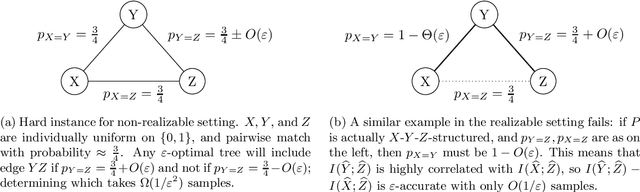
We provide finite sample guarantees for the classical Chow-Liu algorithm (IEEE Trans.~Inform.~Theory, 1968) to learn a tree-structured graphical model of a distribution. For a distribution $P$ on $\Sigma^n$ and a tree $T$ on $n$ nodes, we say $T$ is an $\varepsilon$-approximate tree for $P$ if there is a $T$-structured distribution $Q$ such that $D(P\;||\;Q)$ is at most $\varepsilon$ more than the best possible tree-structured distribution for $P$. We show that if $P$ itself is tree-structured, then the Chow-Liu algorithm with the plug-in estimator for mutual information with $\widetilde{O}(|\Sigma|^3 n\varepsilon^{-1})$ i.i.d.~samples outputs an $\varepsilon$-approximate tree for $P$ with constant probability. In contrast, for a general $P$ (which may not be tree-structured), $\Omega(n^2\varepsilon^{-2})$ samples are necessary to find an $\varepsilon$-approximate tree. Our upper bound is based on a new conditional independence tester that addresses an open problem posed by Canonne, Diakonikolas, Kane, and Stewart~(STOC, 2018): we prove that for three random variables $X,Y,Z$ each over $\Sigma$, testing if $I(X; Y \mid Z)$ is $0$ or $\geq \varepsilon$ is possible with $\widetilde{O}(|\Sigma|^3/\varepsilon)$ samples. Finally, we show that for a specific tree $T$, with $\widetilde{O} (|\Sigma|^2n\varepsilon^{-1})$ samples from a distribution $P$ over $\Sigma^n$, one can efficiently learn the closest $T$-structured distribution in KL divergence by applying the add-1 estimator at each node.

Optimal Testing of Discrete Distributions with High Probability

We study the problem of testing discrete distributions with a focus on the high probability regime. Specifically, given samples from one or more discrete distributions, a property $\mathcal{P}$, and parameters $0< \epsilon, \delta <1$, we want to distinguish {\em with probability at least $1-\delta$} whether these distributions satisfy $\mathcal{P}$ or are $\epsilon$-far from $\mathcal{P}$ in total variation distance. Most prior work in distribution testing studied the constant confidence case (corresponding to $\delta = \Omega(1)$), and provided sample-optimal testers for a range of properties. While one can always boost the confidence probability of any such tester by black-box amplification, this generic boosting method typically leads to sub-optimal sample bounds. Here we study the following broad question: For a given property $\mathcal{P}$, can we {\em characterize} the sample complexity of testing $\mathcal{P}$ as a function of all relevant problem parameters, including the error probability $\delta$? Prior to this work, uniformity testing was the only statistical task whose sample complexity had been characterized in this setting. As our main results, we provide the first algorithms for closeness and independence testing that are sample-optimal, within constant factors, as a function of all relevant parameters. We also show matching information-theoretic lower bounds on the sample complexity of these problems. Our techniques naturally extend to give optimal testers for related problems. To illustrate the generality of our methods, we give optimal algorithms for testing collections of distributions and testing closeness with unequal sized samples.

Lower Bounds for Compressed Sensing with Generative Models

The goal of compressed sensing is to learn a structured signal $x$ from a limited number of noisy linear measurements $y \approx Ax$. In traditional compressed sensing, "structure" is represented by sparsity in some known basis. Inspired by the success of deep learning in modeling images, recent work starting with~\cite{BJPD17} has instead considered structure to come from a generative model $G: \mathbb{R}^k \to \mathbb{R}^n$. We present two results establishing the difficulty of this latter task, showing that existing bounds are tight. First, we provide a lower bound matching the~\cite{BJPD17} upper bound for compressed sensing from $L$-Lipschitz generative models $G$. In particular, there exists such a function that requires roughly $\Omega(k \log L)$ linear measurements for sparse recovery to be possible. This holds even for the more relaxed goal of \emph{nonuniform} recovery. Second, we show that generative models generalize sparsity as a representation of structure. In particular, we construct a ReLU-based neural network $G: \mathbb{R}^{2k} \to \mathbb{R}^n$ with $O(1)$ layers and $O(kn)$ activations per layer, such that the range of $G$ contains all $k$-sparse vectors.