Point Prediction for Streaming Data

We present two new approaches for point prediction with streaming data. One is based on the Count-Min sketch (CMS) and the other is based on Gaussian process priors with a random bias. These methods are intended for the most general predictive problems where no true model can be usefully formulated for the data stream. In statistical contexts, this is often called the $\mathcal{M}$-open problem class. Under the assumption that the data consists of i.i.d samples from a fixed distribution function $F$, we show that the CMS-based estimates of the distribution function are consistent. We compare our new methods with two established predictors in terms of cumulative $L^1$ error. One is based on the Shtarkov solution (often called the normalized maximum likelihood) in the normal experts setting and the other is based on Dirichlet process priors. These comparisons are for two cases. The first is one-pass meaning that the updating of the predictors is done using the fact that the CMS is a sketch. For predictors that are not one-pass, we use streaming $K$-means to give a representative subset of fixed size that can be updated as data accumulate. Preliminary computational work suggests that the one-pass median version of the CMS method is rarely outperformed by the other methods for sufficiently complex data. We also find that predictors based on Gaussian process priors with random biases perform well. The Shtarkov predictors we use here did not perform as well probably because we were only using the simplest example. The other predictors seemed to perform well mainly when the data did not look like they came from an M-open data generator.

Distribution Learning Meets Graph Structure Sampling

This work establishes a novel link between the problem of PAC-learning high-dimensional graphical models and the task of (efficient) counting and sampling of graph structures, using an online learning framework. We observe that if we apply the exponentially weighted average (EWA) or randomized weighted majority (RWM) forecasters on a sequence of samples from a distribution P using the log loss function, the average regret incurred by the forecaster's predictions can be used to bound the expected KL divergence between P and the predictions. Known regret bounds for EWA and RWM then yield new sample complexity bounds for learning Bayes nets. Moreover, these algorithms can be made computationally efficient for several interesting classes of Bayes nets. Specifically, we give a new sample-optimal and polynomial time learning algorithm with respect to trees of unknown structure and the first polynomial sample and time algorithm for learning with respect to Bayes nets over a given chordal skeleton.

Total Variation Distance Estimation Is as Easy as Probabilistic Inference

In this paper, we establish a novel connection between total variation (TV) distance estimation and probabilistic inference. In particular, we present an efficient, structure-preserving reduction from relative approximation of TV distance to probabilistic inference over directed graphical models. This reduction leads to a fully polynomial randomized approximation scheme (FPRAS) for estimating TV distances between distributions over any class of Bayes nets for which there is an efficient probabilistic inference algorithm. In particular, it leads to an FPRAS for estimating TV distances between distributions that are defined by Bayes nets of bounded treewidth. Prior to this work, such approximation schemes only existed for estimating TV distances between product distributions. Our approach employs a new notion of $partial$ couplings of high-dimensional distributions, which might be of independent interest.

List and Certificate Complexities in Replicable Learning

We investigate replicable learning algorithms. Ideally, we would like to design algorithms that output the same canonical model over multiple runs, even when different runs observe a different set of samples from the unknown data distribution. In general, such a strong notion of replicability is not achievable. Thus we consider two feasible notions of replicability called list replicability and certificate replicability. Intuitively, these notions capture the degree of (non) replicability. We design algorithms for certain learning problems that are optimal in list and certificate complexity. We establish matching impossibility results.

Efficient inference of interventional distributions

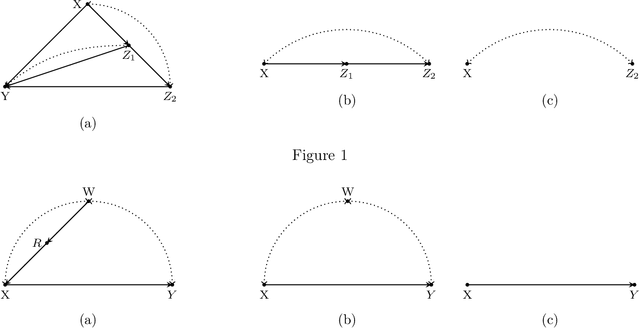
We consider the problem of efficiently inferring interventional distributions in a causal Bayesian network from a finite number of observations. Let $\mathcal{P}$ be a causal model on a set $\mathbf{V}$ of observable variables on a given causal graph $G$. For sets $\mathbf{X},\mathbf{Y}\subseteq \mathbf{V}$, and setting ${\bf x}$ to $\mathbf{X}$, let $P_{\bf x}(\mathbf{Y})$ denote the interventional distribution on $\mathbf{Y}$ with respect to an intervention ${\bf x}$ to variables ${\bf x}$. Shpitser and Pearl (AAAI 2006), building on the work of Tian and Pearl (AAAI 2001), gave an exact characterization of the class of causal graphs for which the interventional distribution $P_{\bf x}({\mathbf{Y}})$ can be uniquely determined. We give the first efficient version of the Shpitser-Pearl algorithm. In particular, under natural assumptions, we give a polynomial-time algorithm that on input a causal graph $G$ on observable variables $\mathbf{V}$, a setting ${\bf x}$ of a set $\mathbf{X} \subseteq \mathbf{V}$ of bounded size, outputs succinct descriptions of both an evaluator and a generator for a distribution $\hat{P}$ that is $\varepsilon$-close (in total variation distance) to $P_{\bf x}({\mathbf{Y}})$ where $Y=\mathbf{V}\setminus \mathbf{X}$, if $P_{\bf x}(\mathbf{Y})$ is identifiable. We also show that when $\mathbf{Y}$ is an arbitrary set, there is no efficient algorithm that outputs an evaluator of a distribution that is $\varepsilon$-close to $P_{\bf x}({\mathbf{Y}})$ unless all problems that have statistical zero-knowledge proofs, including the Graph Isomorphism problem, have efficient randomized algorithms.

Testing Product Distributions: A Closer Look

We study the problems of identity and closeness testing of $n$-dimensional product distributions. Prior works by Canonne, Diakonikolas, Kane and Stewart (COLT 2017) and Daskalakis and Pan (COLT 2017) have established tight sample complexity bounds for non-tolerant testing over a binary alphabet: given two product distributions $P$ and $Q$ over a binary alphabet, distinguish between the cases $P = Q$ and $d_{\mathrm{TV}}(P, Q) > \epsilon$. We build on this prior work to give a more comprehensive map of the complexity of testing of product distributions by investigating tolerant testing with respect to several natural distance measures and over an arbitrary alphabet. Our study gives a fine-grained understanding of how the sample complexity of tolerant testing varies with the distance measures for product distributions. In addition, we also extend one of our upper bounds on product distributions to bounded-degree Bayes nets.

Near-Optimal Learning of Tree-Structured Distributions by Chow-Liu

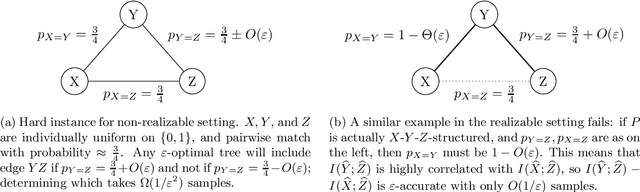
We provide finite sample guarantees for the classical Chow-Liu algorithm (IEEE Trans.~Inform.~Theory, 1968) to learn a tree-structured graphical model of a distribution. For a distribution $P$ on $\Sigma^n$ and a tree $T$ on $n$ nodes, we say $T$ is an $\varepsilon$-approximate tree for $P$ if there is a $T$-structured distribution $Q$ such that $D(P\;||\;Q)$ is at most $\varepsilon$ more than the best possible tree-structured distribution for $P$. We show that if $P$ itself is tree-structured, then the Chow-Liu algorithm with the plug-in estimator for mutual information with $\widetilde{O}(|\Sigma|^3 n\varepsilon^{-1})$ i.i.d.~samples outputs an $\varepsilon$-approximate tree for $P$ with constant probability. In contrast, for a general $P$ (which may not be tree-structured), $\Omega(n^2\varepsilon^{-2})$ samples are necessary to find an $\varepsilon$-approximate tree. Our upper bound is based on a new conditional independence tester that addresses an open problem posed by Canonne, Diakonikolas, Kane, and Stewart~(STOC, 2018): we prove that for three random variables $X,Y,Z$ each over $\Sigma$, testing if $I(X; Y \mid Z)$ is $0$ or $\geq \varepsilon$ is possible with $\widetilde{O}(|\Sigma|^3/\varepsilon)$ samples. Finally, we show that for a specific tree $T$, with $\widetilde{O} (|\Sigma|^2n\varepsilon^{-1})$ samples from a distribution $P$ over $\Sigma^n$, one can efficiently learn the closest $T$-structured distribution in KL divergence by applying the add-1 estimator at each node.

Efficient Distance Approximation for Structured High-Dimensional Distributions via Learning

We design efficient distance approximation algorithms for several classes of structured high-dimensional distributions. Specifically, we show algorithms for the following problems: - Given sample access to two Bayesian networks $P_1$ and $P_2$ over known directed acyclic graphs $G_1$ and $G_2$ having $n$ nodes and bounded in-degree, approximate $d_{tv}(P_1,P_2)$ to within additive error $\epsilon$ using $poly(n,\epsilon)$ samples and time - Given sample access to two ferromagnetic Ising models $P_1$ and $P_2$ on $n$ variables with bounded width, approximate $d_{tv}(P_1, P_2)$ to within additive error $\epsilon$ using $poly(n,\epsilon)$ samples and time - Given sample access to two $n$-dimensional Gaussians $P_1$ and $P_2$, approximate $d_{tv}(P_1, P_2)$ to within additive error $\epsilon$ using $poly(n,\epsilon)$ samples and time - Given access to observations from two causal models $P$ and $Q$ on $n$ variables that are defined over known causal graphs, approximate $d_{tv}(P_a, Q_a)$ to within additive error $\epsilon$ using $poly(n,\epsilon)$ samples, where $P_a$ and $Q_a$ are the interventional distributions obtained by the intervention $do(A=a)$ on $P$ and $Q$ respectively for a particular variable $A$. Our results are the first efficient distance approximation algorithms for these well-studied problems. They are derived using a simple and general connection to distribution learning algorithms. The distance approximation algorithms imply new efficient algorithms for {\em tolerant} testing of closeness of the above-mentioned structured high-dimensional distributions.

Efficiently Learning and Sampling Interventional Distributions from Observations

We study the problem of efficiently estimating the effect of an intervention on a single variable using observational samples in a causal Bayesian network. Our goal is to give algorithms that are efficient in both time and sample complexity in a non-parametric setting. Tian and Pearl (AAAI `02) have exactly characterized the class of causal graphs for which causal effects of atomic interventions can be identified from observational data. We make their result quantitative. Suppose P is a causal model on a set V of n observable variables with respect to a given causal graph G with observable distribution $P$. Let $P_x$ denote the interventional distribution over the observables with respect to an intervention of a designated variable X with x. We show that assuming that G has bounded in-degree, bounded c-components, and that the observational distribution is identifiable and satisfies certain strong positivity condition: 1. [Evaluation] There is an algorithm that outputs with probability $2/3$ an evaluator for a distribution $P'$ that satisfies $d_{tv}(P_x, P') \leq \epsilon$ using $m=\tilde{O}(n\epsilon^{-2})$ samples from $P$ and $O(mn)$ time. The evaluator can return in $O(n)$ time the probability $P'(v)$ for any assignment $v$ to $V$. 2. [Generation] There is an algorithm that outputs with probability $2/3$ a sampler for a distribution $\hat{P}$ that satisfies $d_{tv}(P_x, \hat{P}) \leq \epsilon$ using $m=\tilde{O}(n\epsilon^{-2})$ samples from $P$ and $O(mn)$ time. The sampler returns an iid sample from $\hat{P}$ with probability $1-\delta$ in $O(n\epsilon^{-1} \log\delta^{-1})$ time. We extend our techniques to estimate marginals $P_x|_Y$ over a given $Y \subset V$ of interest. We also show lower bounds for the sample complexity showing that our sample complexity has optimal dependence on the parameters n and $\epsilon$ as well as the strong positivity parameter.

Resource-bounded Dimension in Computational Learning Theory

This paper focuses on the relation between computational learning theory and resource-bounded dimension. We intend to establish close connections between the learnability/nonlearnability of a concept class and its corresponding size in terms of effective dimension, which will allow the use of powerful dimension techniques in computational learning and viceversa, the import of learning results into complexity via dimension. Firstly, we obtain a tight result on the dimension of online mistake-bound learnable classes. Secondly, in relation with PAC learning, we show that the polynomial-space dimension of PAC learnable classes of concepts is zero. This provides a hypothesis on effective dimension that implies the inherent unpredictability of concept classes (the classes that verify this property are classes not efficiently PAC learnable using any hypothesis). Thirdly, in relation to space dimension of classes that are learnable by membership query algorithms, the main result proves that polynomial-space dimension of concept classes learnable by a membership-query algorithm is zero.