Fast Rates for Maximum Entropy Exploration

We consider the reinforcement learning (RL) setting, in which the agent has to act in unknown environment driven by a Markov Decision Process (MDP) with sparse or even reward free signals. In this situation, exploration becomes the main challenge. In this work, we study the maximum entropy exploration problem of two different types. The first type is visitation entropy maximization that was previously considered by Hazan et al. (2019) in the discounted setting. For this type of exploration, we propose an algorithm based on a game theoretic representation that has $\widetilde{\mathcal{O}}(H^3 S^2 A / \varepsilon^2)$ sample complexity thus improving the $\varepsilon$-dependence of Hazan et al. (2019), where $S$ is a number of states, $A$ is a number of actions, $H$ is an episode length, and $\varepsilon$ is a desired accuracy. The second type of entropy we study is the trajectory entropy. This objective function is closely related to the entropy-regularized MDPs, and we propose a simple modification of the UCBVI algorithm that has a sample complexity of order $\widetilde{\mathcal{O}}(1/\varepsilon)$ ignoring dependence in $S, A, H$. Interestingly enough, it is the first theoretical result in RL literature establishing that the exploration problem for the regularized MDPs can be statistically strictly easier (in terms of sample complexity) than for the ordinary MDPs.

Rosenthal-type inequalities for linear statistics of Markov chains

In this paper, we establish novel deviation bounds for additive functionals of geometrically ergodic Markov chains similar to Rosenthal and Bernstein-type inequalities for sums of independent random variables. We pay special attention to the dependence of our bounds on the mixing time of the corresponding chain. Our proof technique is, as far as we know, new and based on the recurrent application of the Poisson decomposition. We relate the constants appearing in our moment bounds to the constants from the martingale version of the Rosenthal inequality and show an explicit dependence on the parameters of the underlying Markov kernel.

Stochastic Approximation Beyond Gradient for Signal Processing and Machine Learning

Stochastic approximation (SA) is a classical algorithm that has had since the early days a huge impact on signal processing, and nowadays on machine learning, due to the necessity to deal with a large amount of data observed with uncertainties. An exemplar special case of SA pertains to the popular stochastic (sub)gradient algorithm which is the working horse behind many important applications. A lesser-known fact is that the SA scheme also extends to non-stochastic-gradient algorithms such as compressed stochastic gradient, stochastic expectation-maximization, and a number of reinforcement learning algorithms. The aim of this article is to overview and introduce the non-stochastic-gradient perspectives of SA to the signal processing and machine learning audiences through presenting a design guideline of SA algorithms backed by theories. Our central theme is to propose a general framework that unifies existing theories of SA, including its non-asymptotic and asymptotic convergence results, and demonstrate their applications on popular non-stochastic-gradient algorithms. We build our analysis framework based on classes of Lyapunov functions that satisfy a variety of mild conditions. We draw connections between non-stochastic-gradient algorithms and scenarios when the Lyapunov function is smooth, convex, or strongly convex. Using the said framework, we illustrate the convergence properties of the non-stochastic-gradient algorithms using concrete examples. Extensions to the emerging variance reduction techniques for improved sample complexity will also be discussed.

State and parameter learning with PaRIS particle Gibbs

Non-linear state-space models, also known as general hidden Markov models, are ubiquitous in statistical machine learning, being the most classical generative models for serial data and sequences in general. The particle-based, rapid incremental smoother PaRIS is a sequential Monte Carlo (SMC) technique allowing for efficient online approximation of expectations of additive functionals under the smoothing distribution in these models. Such expectations appear naturally in several learning contexts, such as likelihood estimation (MLE) and Markov score climbing (MSC). PARIS has linear computational complexity, limited memory requirements and comes with non-asymptotic bounds, convergence results and stability guarantees. Still, being based on self-normalised importance sampling, the PaRIS estimator is biased. Our first contribution is to design a novel additive smoothing algorithm, the Parisian particle Gibbs PPG sampler, which can be viewed as a PaRIS algorithm driven by conditional SMC moves, resulting in bias-reduced estimates of the targeted quantities. We substantiate the PPG algorithm with theoretical results, including new bounds on bias and variance as well as deviation inequalities. Our second contribution is to apply PPG in a learning framework, covering MLE and MSC as special examples. In this context, we establish, under standard assumptions, non-asymptotic bounds highlighting the value of bias reduction and the implicit Rao--Blackwellization of PPG. These are the first non-asymptotic results of this kind in this setting. We illustrate our theoretical results with numerical experiments supporting our claims.

Stochastic Variable Metric Proximal Gradient with variance reduction for non-convex composite optimization

This paper introduces a novel algorithm, the Perturbed Proximal Preconditioned SPIDER algorithm (3P-SPIDER), designed to solve finite sum non-convex composite optimization. It is a stochastic Variable Metric Forward-Backward algorithm, which allows approximate preconditioned forward operator and uses a variable metric proximity operator as the backward operator; it also proposes a mini-batch strategy with variance reduction to address the finite sum setting. We show that 3P-SPIDER extends some Stochastic preconditioned Gradient Descent-based algorithms and some Incremental Expectation Maximization algorithms to composite optimization and to the case the forward operator can not be computed in closed form. We also provide an explicit control of convergence in expectation of 3P-SPIDER, and study its complexity in order to satisfy the epsilon-approximate stationary condition. Our results are the first to combine the composite non-convex optimization setting, a variance reduction technique to tackle the finite sum setting by using a minibatch strategy and, to allow deterministic or random approximations of the preconditioned forward operator. Finally, through an application to inference in a logistic regression model with random effects, we numerically compare 3P-SPIDER to other stochastic forward-backward algorithms and discuss the role of some design parameters of 3P-SPIDER.

AskewSGD : An Annealed interval-constrained Optimisation method to train Quantized Neural Networks

In this paper, we develop a new algorithm, Annealed Skewed SGD - AskewSGD - for training deep neural networks (DNNs) with quantized weights. First, we formulate the training of quantized neural networks (QNNs) as a smoothed sequence of interval-constrained optimization problems. Then, we propose a new first-order stochastic method, AskewSGD, to solve each constrained optimization subproblem. Unlike algorithms with active sets and feasible directions, AskewSGD avoids projections or optimization under the entire feasible set and allows iterates that are infeasible. The numerical complexity of AskewSGD is comparable to existing approaches for training QNNs, such as the straight-through gradient estimator used in BinaryConnect, or other state of the art methods (ProxQuant, LUQ). We establish convergence guarantees for AskewSGD (under general assumptions for the objective function). Experimental results show that the AskewSGD algorithm performs better than or on par with state of the art methods in classical benchmarks.

Federated Averaging Langevin Dynamics: Toward a unified theory and new algorithms

This paper focuses on Bayesian inference in a federated learning context (FL). While several distributed MCMC algorithms have been proposed, few consider the specific limitations of FL such as communication bottlenecks and statistical heterogeneity. Recently, Federated Averaging Langevin Dynamics (FALD) was introduced, which extends the Federated Averaging algorithm to Bayesian inference. We obtain a novel tight non-asymptotic upper bound on the Wasserstein distance to the global posterior for FALD. This bound highlights the effects of statistical heterogeneity, which causes a drift in the local updates that negatively impacts convergence. We propose a new algorithm VR-FALD* that uses control variates to correct the client drift. We establish non-asymptotic bounds showing that VR-FALD* is not affected by statistical heterogeneity. Finally, we illustrate our results on several FL benchmarks for Bayesian inference.

Optimistic Posterior Sampling for Reinforcement Learning with Few Samples and Tight Guarantees

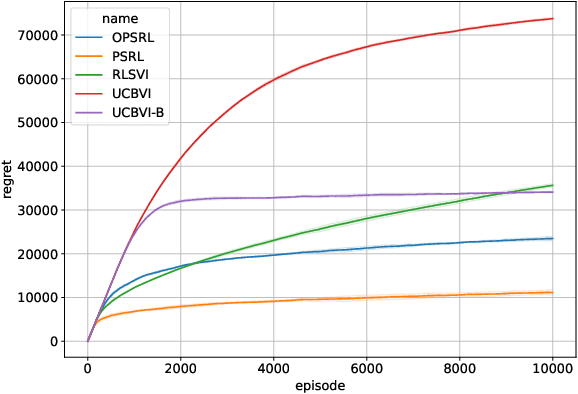
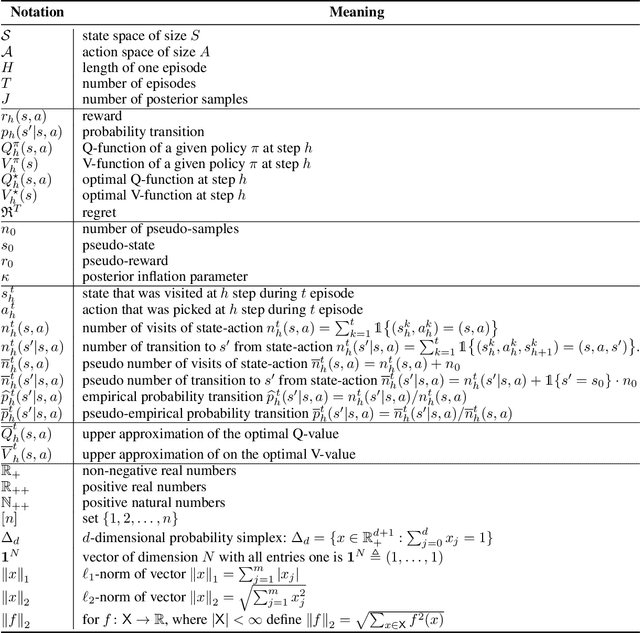
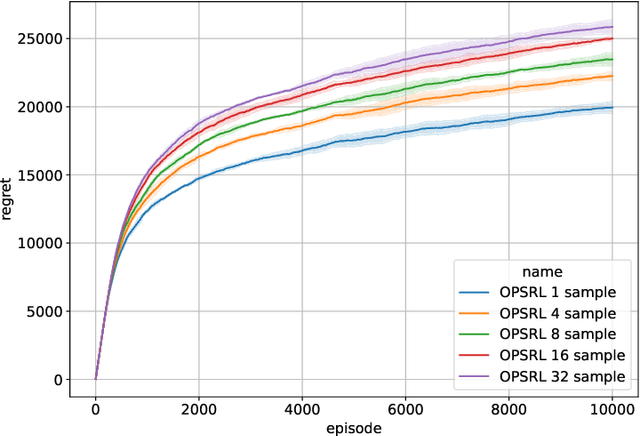
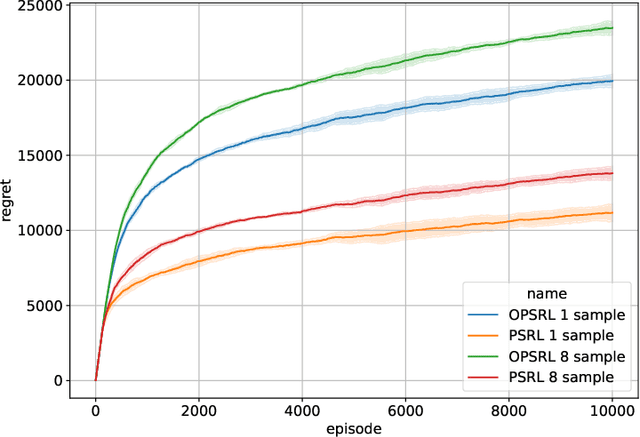
We consider reinforcement learning in an environment modeled by an episodic, finite, stage-dependent Markov decision process of horizon $H$ with $S$ states, and $A$ actions. The performance of an agent is measured by the regret after interacting with the environment for $T$ episodes. We propose an optimistic posterior sampling algorithm for reinforcement learning (OPSRL), a simple variant of posterior sampling that only needs a number of posterior samples logarithmic in $H$, $S$, $A$, and $T$ per state-action pair. For OPSRL we guarantee a high-probability regret bound of order at most $\widetilde{\mathcal{O}}(\sqrt{H^3SAT})$ ignoring $\text{poly}\log(HSAT)$ terms. The key novel technical ingredient is a new sharp anti-concentration inequality for linear forms which may be of independent interest. Specifically, we extend the normal approximation-based lower bound for Beta distributions by Alfers and Dinges [1984] to Dirichlet distributions. Our bound matches the lower bound of order $\Omega(\sqrt{H^3SAT})$, thereby answering the open problems raised by Agrawal and Jia [2017b] for the episodic setting.

BR-SNIS: Bias Reduced Self-Normalized Importance Sampling

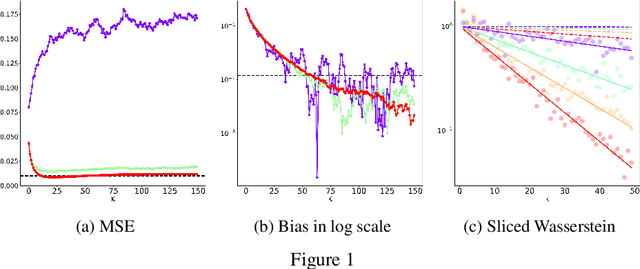
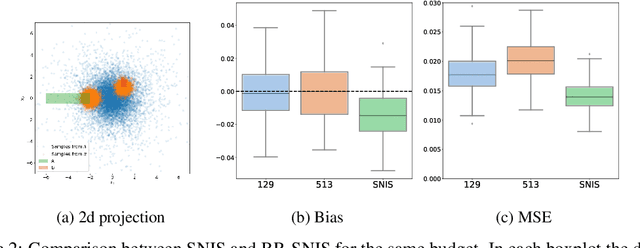
Importance Sampling (IS) is a method for approximating expectations under a target distribution using independent samples from a proposal distribution and the associated importance weights. In many applications, the target distribution is known only up to a normalization constant, in which case self-normalized IS (SNIS) can be used. While the use of self-normalization can have a positive effect on the dispersion of the estimator, it introduces bias. In this work, we propose a new method, BR-SNIS, whose complexity is essentially the same as that of SNIS and which significantly reduces bias without increasing the variance. This method is a wrapper in the sense that it uses the same proposal samples and importance weights as SNIS, but makes clever use of iterated sampling--importance resampling (ISIR) to form a bias-reduced version of the estimator. We furnish the proposed algorithm with rigorous theoretical results, including new bias, variance and high-probability bounds, and these are illustrated by numerical examples.

Finite-time High-probability Bounds for Polyak-Ruppert Averaged Iterates of Linear Stochastic Approximation

This paper provides a finite-time analysis of linear stochastic approximation (LSA) algorithms with fixed step size, a core method in statistics and machine learning. LSA is used to compute approximate solutions of a $d$-dimensional linear system $\bar{\mathbf{A}} \theta = \bar{\mathbf{b}}$, for which $(\bar{\mathbf{A}}, \bar{\mathbf{b}})$ can only be estimated through (asymptotically) unbiased observations $\{(\mathbf{A}(Z_n),\mathbf{b}(Z_n))\}_{n \in \mathbb{N}}$. We consider here the case where $\{Z_n\}_{n \in \mathbb{N}}$ is an i.i.d. sequence or a uniformly geometrically ergodic Markov chain, and derive $p$-moments inequality and high probability bounds for the iterates defined by LSA and its Polyak-Ruppert averaged version. More precisely, we establish bounds of order $(p \alpha t_{\operatorname{mix}})^{1/2}d^{1/p}$ on the $p$-th moment of the last iterate of LSA. In this formula $\alpha$ is the step size of the procedure and $t_{\operatorname{mix}}$ is the mixing time of the underlying chain ($t_{\operatorname{mix}}=1$ in the i.i.d. setting). We then prove finite-time instance-dependent bounds on the Polyak-Ruppert averaged sequence of iterates. These results are sharp in the sense that the leading term we obtain matches the local asymptotic minimax limit, including tight dependence on the parameters $(d,t_{\operatorname{mix}})$ in the higher order terms.