Refined Analysis of Federated Averaging's Bias and Federated Richardson-Romberg Extrapolation

In this paper, we present a novel analysis of FedAvg with constant step size, relying on the Markov property of the underlying process. We demonstrate that the global iterates of the algorithm converge to a stationary distribution and analyze its resulting bias and variance relative to the problem's solution. We provide a first-order expansion of the bias in both homogeneous and heterogeneous settings. Interestingly, this bias decomposes into two distinct components: one that depends solely on stochastic gradient noise and another on client heterogeneity. Finally, we introduce a new algorithm based on the Richardson-Romberg extrapolation technique to mitigate this bias.

Federated UCBVI: Communication-Efficient Federated Regret Minimization with Heterogeneous Agents

In this paper, we present the Federated Upper Confidence Bound Value Iteration algorithm ($\texttt{Fed-UCBVI}$), a novel extension of the $\texttt{UCBVI}$ algorithm (Azar et al., 2017) tailored for the federated learning framework. We prove that the regret of $\texttt{Fed-UCBVI}$ scales as $\tilde{\mathcal{O}}(\sqrt{H^3 |\mathcal{S}| |\mathcal{A}| T / M})$, with a small additional term due to heterogeneity, where $|\mathcal{S}|$ is the number of states, $|\mathcal{A}|$ is the number of actions, $H$ is the episode length, $M$ is the number of agents, and $T$ is the number of episodes. Notably, in the single-agent setting, this upper bound matches the minimax lower bound up to polylogarithmic factors, while in the multi-agent scenario, $\texttt{Fed-UCBVI}$ has linear speed-up. To conduct our analysis, we introduce a new measure of heterogeneity, which may hold independent theoretical interest. Furthermore, we show that, unlike existing federated reinforcement learning approaches, $\texttt{Fed-UCBVI}$'s communication complexity only marginally increases with the number of agents.

SCAFFLSA: Quantifying and Eliminating Heterogeneity Bias in Federated Linear Stochastic Approximation and Temporal Difference Learning

In this paper, we perform a non-asymptotic analysis of the federated linear stochastic approximation (FedLSA) algorithm. We explicitly quantify the bias introduced by local training with heterogeneous agents, and investigate the sample complexity of the algorithm. We show that the communication complexity of FedLSA scales polynomially with the desired precision $\epsilon$, which limits the benefits of federation. To overcome this, we propose SCAFFLSA, a novel variant of FedLSA, that uses control variates to correct the bias of local training, and prove its convergence without assumptions on statistical heterogeneity. We apply the proposed methodology to federated temporal difference learning with linear function approximation, and analyze the corresponding complexity improvements.

The Relative Gaussian Mechanism and its Application to Private Gradient Descent

The Gaussian Mechanism (GM), which consists in adding Gaussian noise to a vector-valued query before releasing it, is a standard privacy protection mechanism. In particular, given that the query respects some L2 sensitivity property (the L2 distance between outputs on any two neighboring inputs is bounded), GM guarantees R\'enyi Differential Privacy (RDP). Unfortunately, precisely bounding the L2 sensitivity can be hard, thus leading to loose privacy bounds. In this work, we consider a Relative L2 sensitivity assumption, in which the bound on the distance between two query outputs may also depend on their norm. Leveraging this assumption, we introduce the Relative Gaussian Mechanism (RGM), in which the variance of the noise depends on the norm of the output. We prove tight bounds on the RDP parameters under relative L2 sensitivity, and characterize the privacy loss incurred by using output-dependent noise. In particular, we show that RGM naturally adapts to a latent variable that would control the norm of the output. Finally, we instantiate our framework to show tight guarantees for Private Gradient Descent, a problem that naturally fits our relative L2 sensitivity assumption.

Fairness Certificates for Differentially Private Classification

In this work, we theoretically study the impact of differential privacy on fairness in binary classification. We prove that, given a class of models, popular group fairness measures are pointwise Lipschitz-continuous with respect to the parameters of the model. This result is a consequence of a more general statement on the probability that a decision function makes a negative prediction conditioned on an arbitrary event (such as membership to a sensitive group), which may be of independent interest. We use the aforementioned Lipschitz property to prove a high probability bound showing that, given enough examples, the fairness level of private models is close to the one of their non-private counterparts.

FLamby: Datasets and Benchmarks for Cross-Silo Federated Learning in Realistic Healthcare Settings

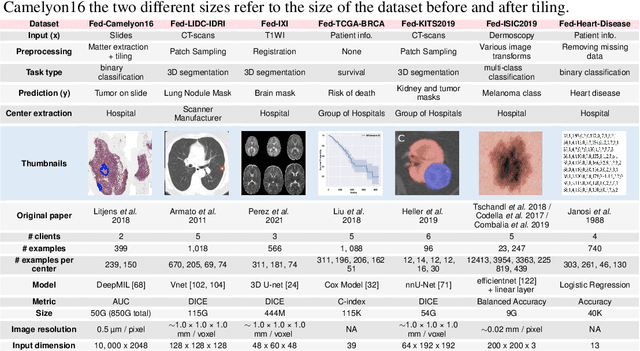
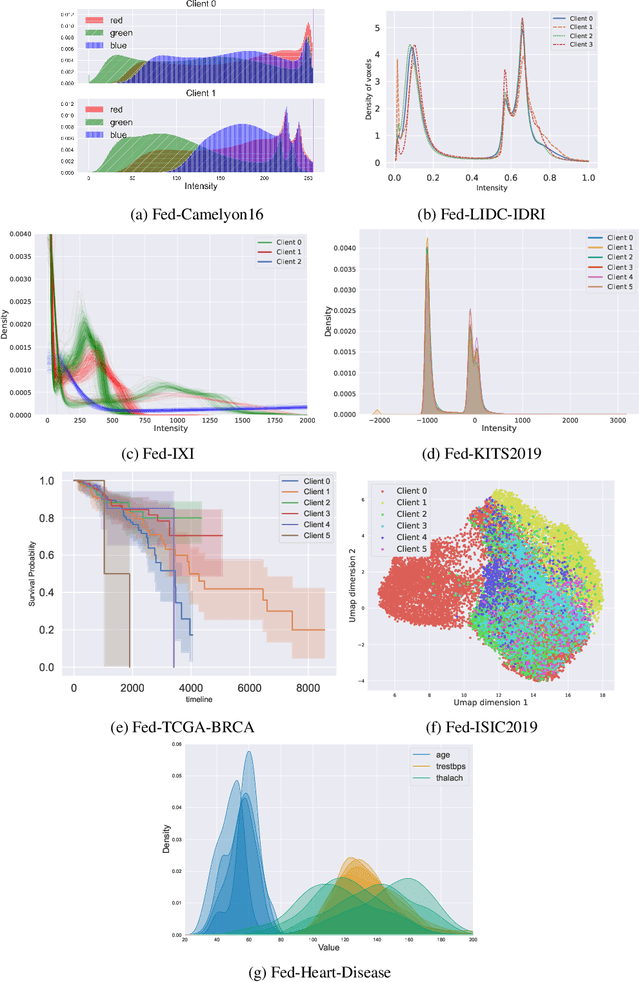
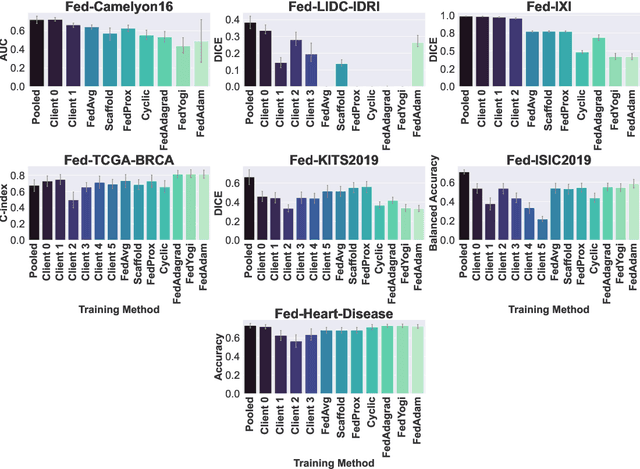
Federated Learning (FL) is a novel approach enabling several clients holding sensitive data to collaboratively train machine learning models, without centralizing data. The cross-silo FL setting corresponds to the case of few ($2$--$50$) reliable clients, each holding medium to large datasets, and is typically found in applications such as healthcare, finance, or industry. While previous works have proposed representative datasets for cross-device FL, few realistic healthcare cross-silo FL datasets exist, thereby slowing algorithmic research in this critical application. In this work, we propose a novel cross-silo dataset suite focused on healthcare, FLamby (Federated Learning AMple Benchmark of Your cross-silo strategies), to bridge the gap between theory and practice of cross-silo FL. FLamby encompasses 7 healthcare datasets with natural splits, covering multiple tasks, modalities, and data volumes, each accompanied with baseline training code. As an illustration, we additionally benchmark standard FL algorithms on all datasets. Our flexible and modular suite allows researchers to easily download datasets, reproduce results and re-use the different components for their research. FLamby is available at~\url{www.github.com/owkin/flamby}.

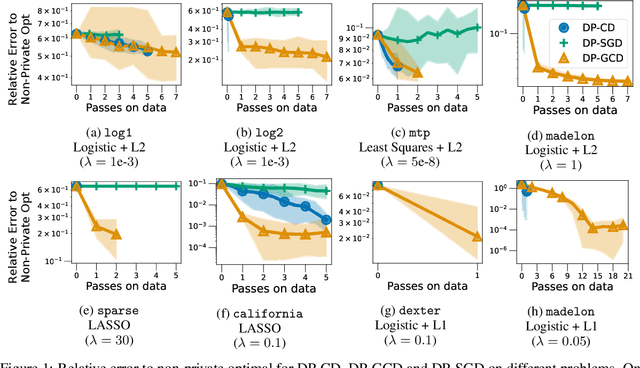
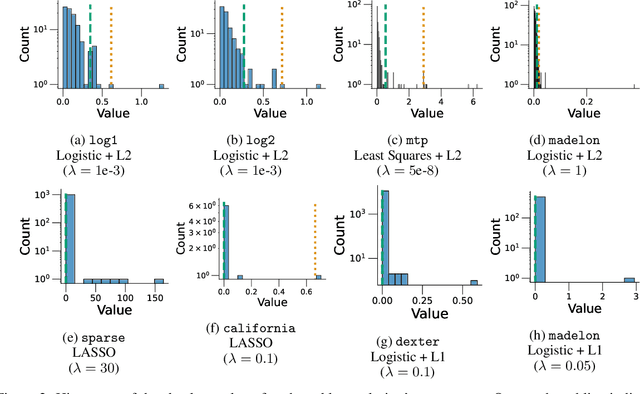
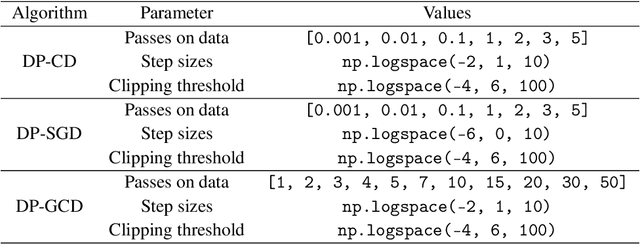
High-Dimensional Private Empirical Risk Minimization by Greedy Coordinate Descent

In this paper, we study differentially private empirical risk minimization (DP-ERM). It has been shown that the (worst-case) utility of DP-ERM reduces as the dimension increases. This is a major obstacle to privately learning large machine learning models. In high dimension, it is common for some model's parameters to carry more information than others. To exploit this, we propose a differentially private greedy coordinate descent (DP-GCD) algorithm. At each iteration, DP-GCD privately performs a coordinate-wise gradient step along the gradients' (approximately) greatest entry. We show theoretically that DP-GCD can improve utility by exploiting structural properties of the problem's solution (such as sparsity or quasi-sparsity), with very fast progress in early iterations. We then illustrate this numerically, both on synthetic and real datasets. Finally, we describe promising directions for future work.

Differentially Private Coordinate Descent for Composite Empirical Risk Minimization

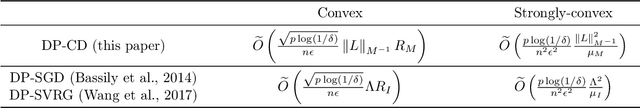
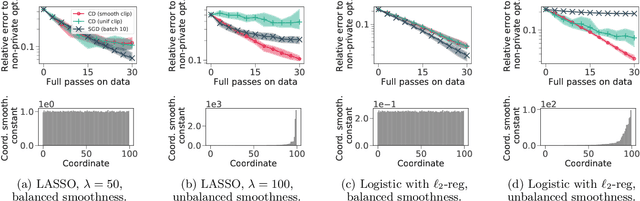
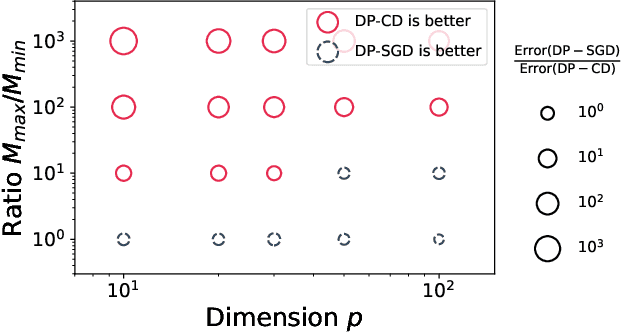
Machine learning models can leak information about the data used to train them. Differentially Private (DP) variants of optimization algorithms like Stochastic Gradient Descent (DP-SGD) have been designed to mitigate this, inducing a trade-off between privacy and utility. In this paper, we propose a new method for composite Differentially Private Empirical Risk Minimization (DP-ERM): Differentially Private proximal Coordinate Descent (DP-CD). We analyze its utility through a novel theoretical analysis of inexact coordinate descent, and highlight some regimes where DP-CD outperforms DP-SGD, thanks to the possibility of using larger step sizes. We also prove new lower bounds for composite DP-ERM under coordinate-wise regularity assumptions, that are, in some settings, nearly matched by our algorithm. In practical implementations, the coordinate-wise nature of DP-CD updates demands special care in choosing the clipping thresholds used to bound individual contributions to the gradients. A natural parameterization of these thresholds emerges from our theory, limiting the addition of unnecessarily large noise without requiring coordinate-wise hyperparameter tuning or extra computational cost.