Natural Quantum Monte Carlo Computation of Excited States

We present a variational Monte Carlo algorithm for estimating the lowest excited states of a quantum system which is a natural generalization of the estimation of ground states. The method has no free parameters and requires no explicit orthogonalization of the different states, instead transforming the problem of finding excited states of a given system into that of finding the ground state of an expanded system. Expected values of arbitrary observables can be calculated, including off-diagonal expectations between different states such as the transition dipole moment. Although the method is entirely general, it works particularly well in conjunction with recent work on using neural networks as variational Ansatze for many-electron systems, and we show that by combining this method with the FermiNet and Psiformer Ansatze we can accurately recover vertical excitation energies and oscillator strengths on molecules as large as benzene. Beyond the examples on molecules presented here, we expect this technique will be of great interest for applications of variational quantum Monte Carlo to atomic, nuclear and condensed matter physics.

Neural Wave Functions for Superfluids

Understanding superfluidity remains a major goal of condensed matter physics. Here we tackle this challenge utilizing the recently developed Fermionic neural network (FermiNet) wave function Ansatz for variational Monte Carlo calculations. We study the unitary Fermi gas, a system with strong, short-range, two-body interactions known to possess a superfluid ground state but difficult to describe quantitively. We demonstrate key limitations of the FermiNet Ansatz in studying the unitary Fermi gas and propose a simple modification that outperforms the original FermiNet significantly, giving highly accurate results. We prove mathematically that the new Ansatz is a strict generalization of the original FermiNet architecture, despite the use of fewer parameters. Our approach shares several advantanges with the FermiNet: the use of a neural network removes the need for an underlying basis set; and the flexiblity of the network yields extremely accurate results within a variational quantum Monte Carlo framework that provides access to unbiased estimates of arbitrary ground-state expectation values. We discuss how the method can be extended to study other superfluids.

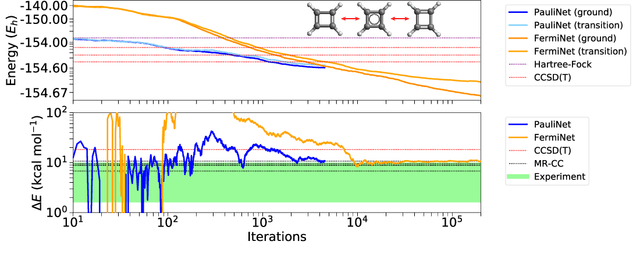
A Self-Attention Ansatz for Ab-initio Quantum Chemistry

We present a novel neural network architecture using self-attention, the Wavefunction Transformer (Psiformer), which can be used as an approximation (or Ansatz) for solving the many-electron Schr\"odinger equation, the fundamental equation for quantum chemistry and material science. This equation can be solved from first principles, requiring no external training data. In recent years, deep neural networks like the FermiNet and PauliNet have been used to significantly improve the accuracy of these first-principle calculations, but they lack an attention-like mechanism for gating interactions between electrons. Here we show that the Psiformer can be used as a drop-in replacement for these other neural networks, often dramatically improving the accuracy of the calculations. On larger molecules especially, the ground state energy can be improved by dozens of kcal/mol, a qualitative leap over previous methods. This demonstrates that self-attention networks can learn complex quantum mechanical correlations between electrons, and are a promising route to reaching unprecedented accuracy in chemical calculations on larger systems.

Learned Force Fields Are Ready For Ground State Catalyst Discovery

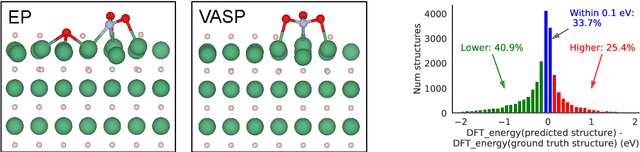
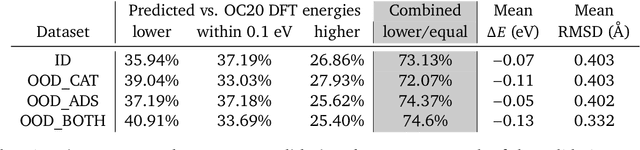
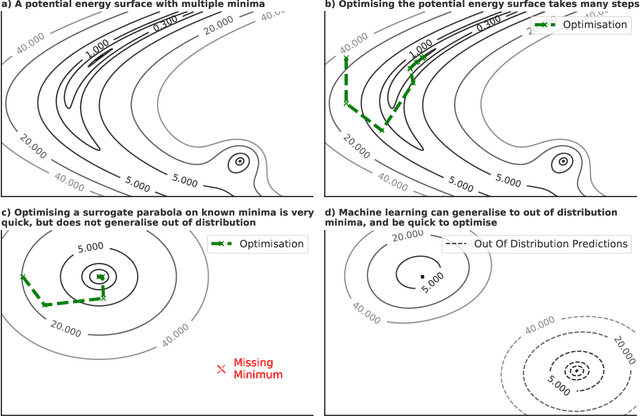
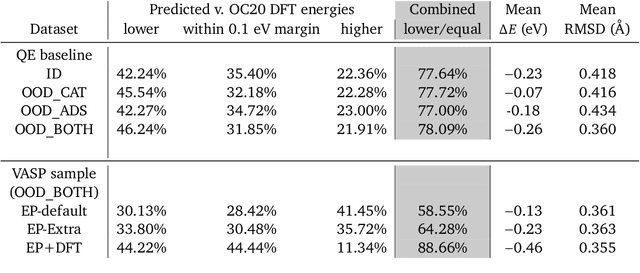
We present evidence that learned density functional theory (``DFT'') force fields are ready for ground state catalyst discovery. Our key finding is that relaxation using forces from a learned potential yields structures with similar or lower energy to those relaxed using the RPBE functional in over 50\% of evaluated systems, despite the fact that the predicted forces differ significantly from the ground truth. This has the surprising implication that learned potentials may be ready for replacing DFT in challenging catalytic systems such as those found in the Open Catalyst 2020 dataset. Furthermore, we show that a force field trained on a locally harmonic energy surface with the same minima as a target DFT energy is also able to find lower or similar energy structures in over 50\% of cases. This ``Easy Potential'' converges in fewer steps than a standard model trained on true energies and forces, which further accelerates calculations. Its success illustrates a key point: learned potentials can locate energy minima even when the model has high force errors. The main requirement for structure optimisation is simply that the learned potential has the correct minima. Since learned potentials are fast and scale linearly with system size, our results open the possibility of quickly finding ground states for large systems.

Better, Faster Fermionic Neural Networks

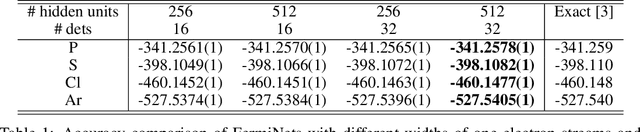
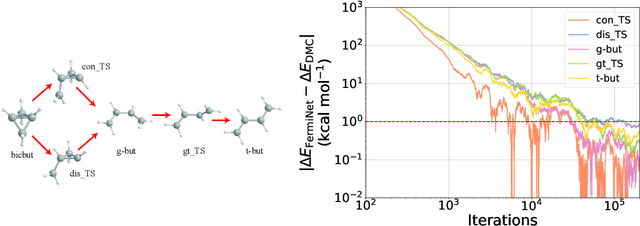
The Fermionic Neural Network (FermiNet) is a recently-developed neural network architecture that can be used as a wavefunction Ansatz for many-electron systems, and has already demonstrated high accuracy on small systems. Here we present several improvements to the FermiNet that allow us to set new records for speed and accuracy on challenging systems. We find that increasing the size of the network is sufficient to reach chemical accuracy on atoms as large as argon. Through a combination of implementing FermiNet in JAX and simplifying several parts of the network, we are able to reduce the number of GPU hours needed to train the FermiNet on large systems by an order of magnitude. This enables us to run the FermiNet on the challenging transition of bicyclobutane to butadiene and compare against the PauliNet on the automerization of cyclobutadiene, and we achieve results near the state of the art for both.

Ab-Initio Solution of the Many-Electron Schrödinger Equation with Deep Neural Networks

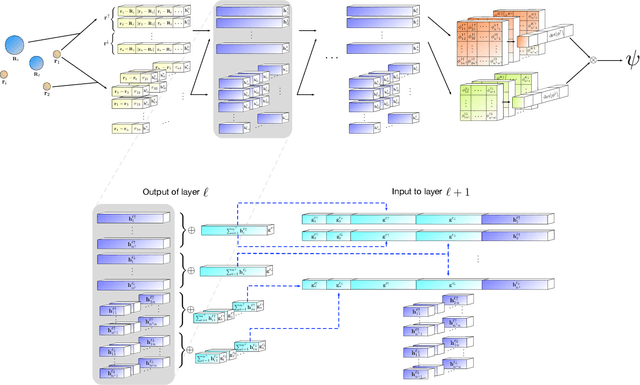
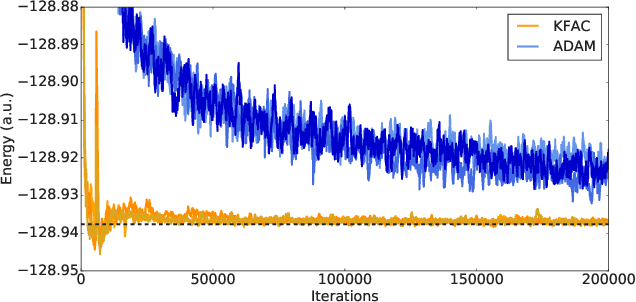
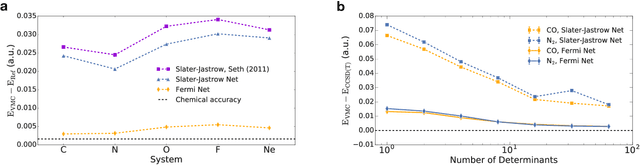
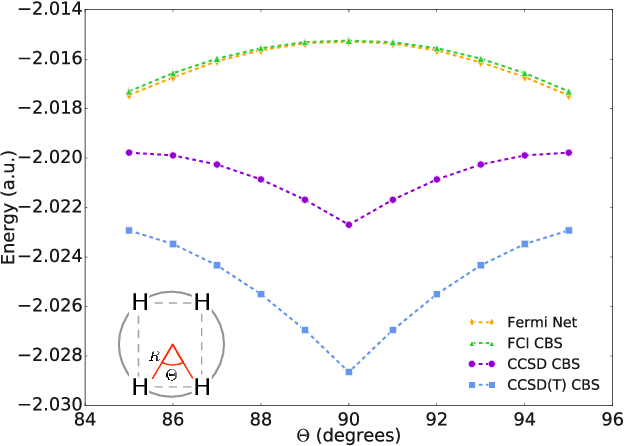
Given access to accurate solutions of the many-electron Schr\"odinger equation, nearly all chemistry could be derived from first principles. Exact wavefunctions of interesting chemical systems are out of reach because they are NP-hard to compute in general, but approximations can be found using polynomially-scaling algorithms. The key challenge for many of these algorithms is the choice of wavefunction approximation, or Ansatz, which must trade off between efficiency and accuracy. Neural networks have shown impressive power as accurate practical function approximators and promise as a compact wavefunction Ansatz for spin systems, but problems in electronic structure require wavefunctions that obey Fermi-Dirac statistics. Here we introduce a novel deep learning architecture, the Fermionic Neural Network, as a powerful wavefunction Ansatz for many-electron systems. The Fermionic Neural Network is able to achieve accuracy beyond other variational Monte Carlo Ans\"atze on a variety of atoms and small molecules. Using no data other than atomic positions and charges, we predict the dissociation curves of the nitrogen molecule and hydrogen chain, two challenging strongly-correlated systems, to significantly higher accuracy than the coupled cluster method, widely considered the gold standard for quantum chemistry. This demonstrates that deep neural networks can outperform existing ab-initio quantum chemistry methods, opening the possibility of accurate direct optimisation of wavefunctions for previously intractable molecules and solids.