Accurate and scalable exchange-correlation with deep learning

Density Functional Theory (DFT) is the most widely used electronic structure method for predicting the properties of molecules and materials. Although DFT is, in principle, an exact reformulation of the Schr\"odinger equation, practical applications rely on approximations to the unknown exchange-correlation (XC) functional. Most existing XC functionals are constructed using a limited set of increasingly complex, hand-crafted features that improve accuracy at the expense of computational efficiency. Yet, no current approximation achieves the accuracy and generality for predictive modeling of laboratory experiments at chemical accuracy -- typically defined as errors below 1 kcal/mol. In this work, we present Skala, a modern deep learning-based XC functional that bypasses expensive hand-designed features by learning representations directly from data. Skala achieves chemical accuracy for atomization energies of small molecules while retaining the computational efficiency typical of semi-local DFT. This performance is enabled by training on an unprecedented volume of high-accuracy reference data generated using computationally intensive wavefunction-based methods. Notably, Skala systematically improves with additional training data covering diverse chemistry. By incorporating a modest amount of additional high-accuracy data tailored to chemistry beyond atomization energies, Skala achieves accuracy competitive with the best-performing hybrid functionals across general main group chemistry, at the cost of semi-local DFT. As the training dataset continues to expand, Skala is poised to further enhance the predictive power of first-principles simulations.

Highly Accurate Real-space Electron Densities with Neural Networks

Variational ab-initio methods in quantum chemistry stand out among other methods in providing direct access to the wave function. This allows in principle straightforward extraction of any other observable of interest, besides the energy, but in practice this extraction is often technically difficult and computationally impractical. Here, we consider the electron density as a central observable in quantum chemistry and introduce a novel method to obtain accurate densities from real-space many-electron wave functions by representing the density with a neural network that captures known asymptotic properties and is trained from the wave function by score matching and noise-contrastive estimation. We use variational quantum Monte Carlo with deep-learning ans\"atze (deep QMC) to obtain highly accurate wave functions free of basis set errors, and from them, using our novel method, correspondingly accurate electron densities, which we demonstrate by calculating dipole moments, nuclear forces, contact densities, and other density-based properties.

Ab-initio quantum chemistry with neural-network wavefunctions

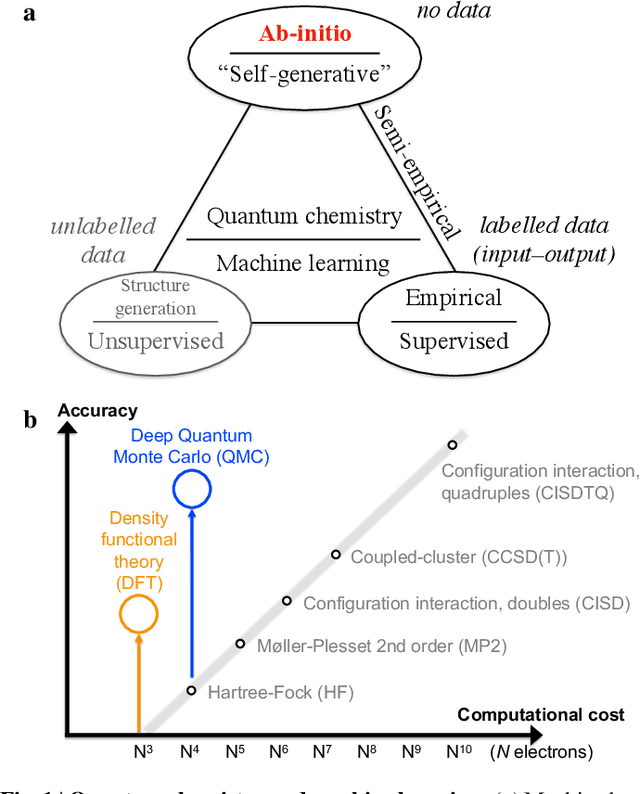
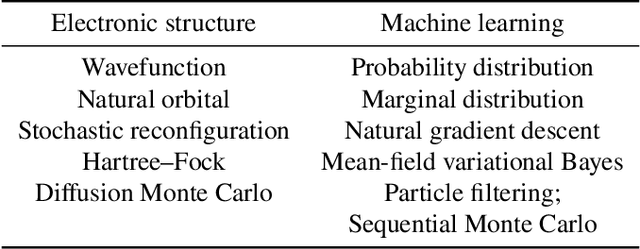
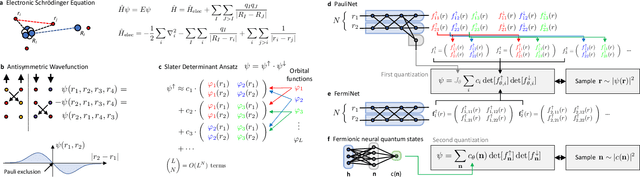
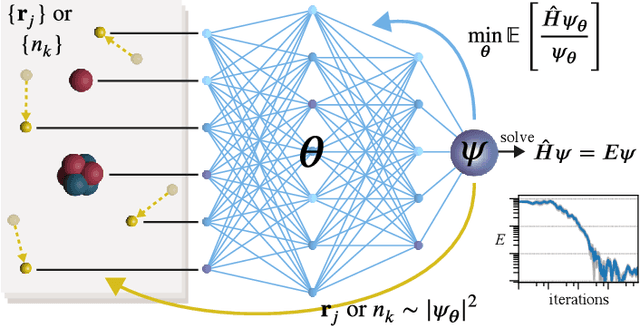
Machine learning and specifically deep-learning methods have outperformed human capabilities in many pattern recognition and data processing problems, in game playing, and now also play an increasingly important role in scientific discovery. A key application of machine learning in the molecular sciences is to learn potential energy surfaces or force fields from ab-initio solutions of the electronic Schr\"odinger equation using datasets obtained with density functional theory, coupled cluster, or other quantum chemistry methods. Here we review a recent and complementary approach: using machine learning to aid the direct solution of quantum chemistry problems from first principles. Specifically, we focus on quantum Monte Carlo (QMC) methods that use neural network ansatz functions in order to solve the electronic Schr\"odinger equation, both in first and second quantization, computing ground and excited states, and generalizing over multiple nuclear configurations. Compared to existing quantum chemistry methods, these new deep QMC methods have the potential to generate highly accurate solutions of the Schr\"odinger equation at relatively modest computational cost.

Electronic excited states in deep variational Monte Carlo

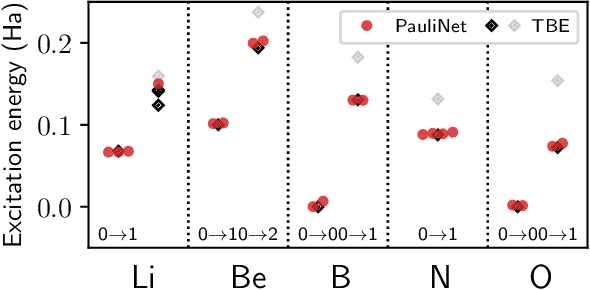
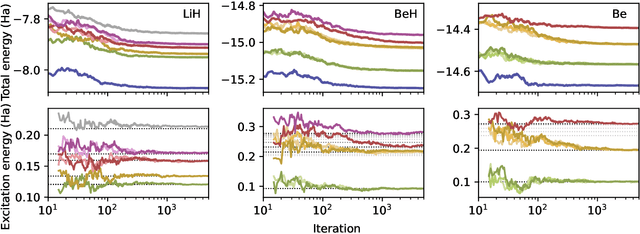
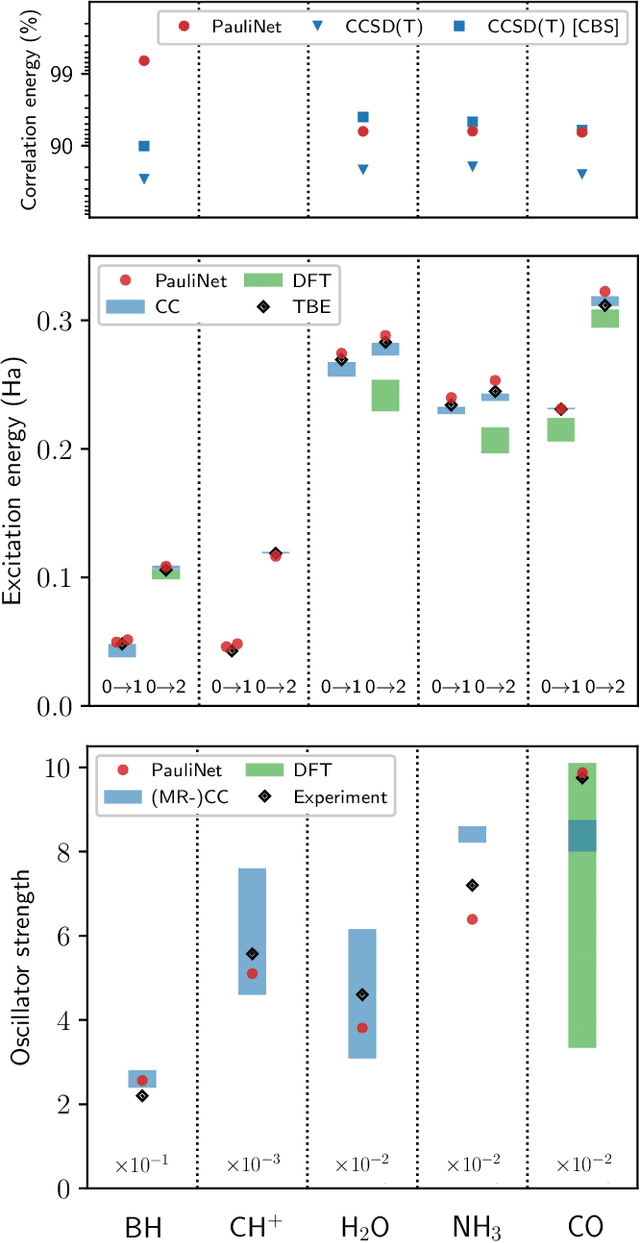
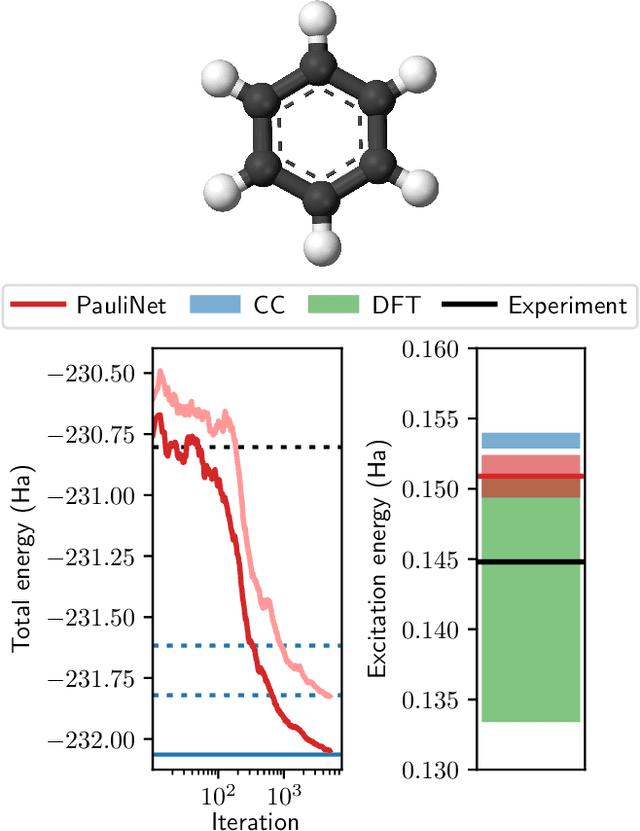
Obtaining accurate ground and low-lying excited states of electronic systems is crucial in a multitude of important applications. One ab initio method for solving the electronic Schr\"odinger equation that scales favorably for large systems and whose accuracy is limited only by the choice of wavefunction ansatz employed is variational quantum Monte Carlo (QMC). The recently introduced deep QMC approach, using a new class of ansatzes represented by deep neural networks, has been shown to generate nearly exact ground-state solutions for molecules containing up to a few dozen electrons, with the potential to scale to much larger systems where other highly accurate methods are not feasible. In this paper, we advance one such ansatz (PauliNet) to compute electronic excited states through a simple variational procedure. We demonstrate our method on a variety of small atoms and molecules where we consistently achieve high accuracy for low-lying states. To highlight the method's potential for larger systems, we show that for the benzene molecule, PauliNet is on par with significantly more expensive high-level electronic structure methods in terms of the excitation energy and outperforms them in terms of absolute energies.

Convergence to the fixed-node limit in deep variational Monte Carlo

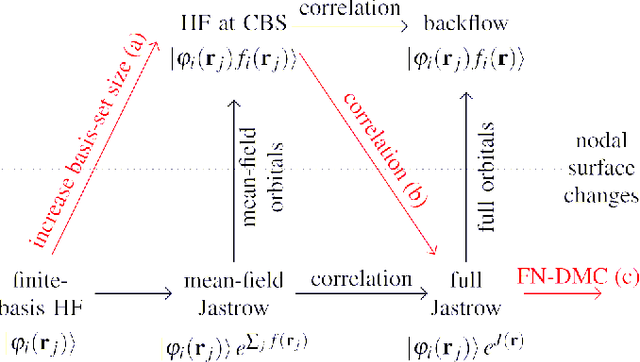
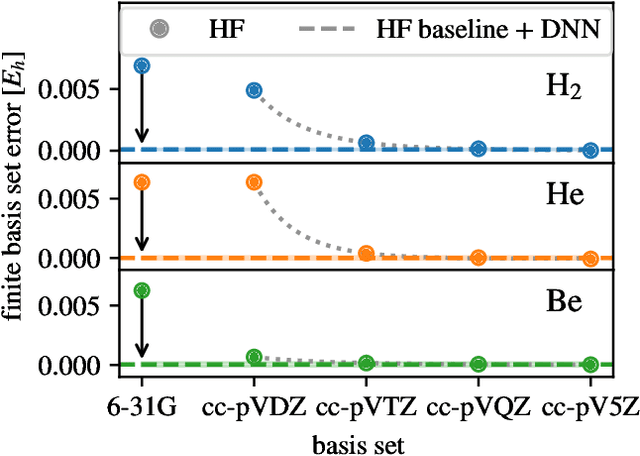
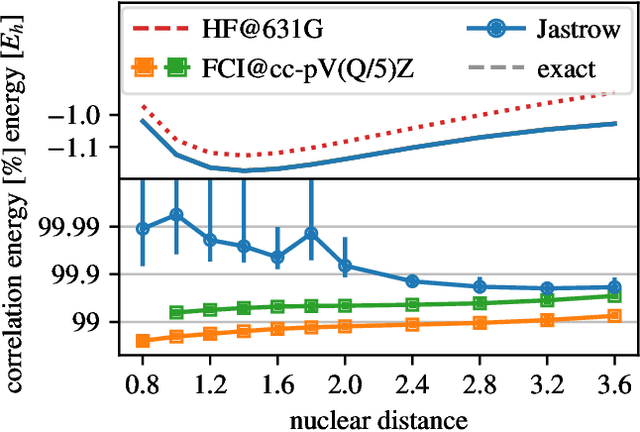
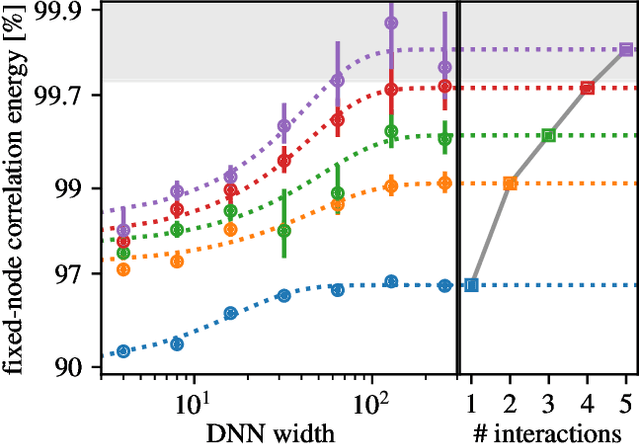
Variational quantum Monte Carlo (QMC) is an ab-initio method for solving the electronic Schr\"odinger equation that is exact in principle, but limited by the flexibility of the available ansatzes in practice. The recently introduced deep QMC approach, specifically two deep-neural-network ansatzes PauliNet and FermiNet, allows variational QMC to reach the accuracy of diffusion QMC, but little is understood about the convergence behavior of such ansatzes. Here, we analyze how deep variational QMC approaches the fixed-node limit with increasing network size. First, we demonstrate that a deep neural network can overcome the limitations of a small basis set and reach the mean-field complete-basis-set limit. Moving to electron correlation, we then perform an extensive hyperparameter scan of a deep Jastrow factor for LiH and H$_4$ and find that variational energies at the fixed-node limit can be obtained with a sufficiently large network. Finally, we benchmark mean-field and many-body ansatzes on H$_2$O, increasing the fraction of recovered fixed-node correlation energy by half an order of magnitude compared to previous VMC results. This analysis helps understanding the superb performance of deep variational ansatzes, and will guide future improvements of the neural network architectures in deep QMC.

Deep neural network solution of the electronic Schrödinger equation

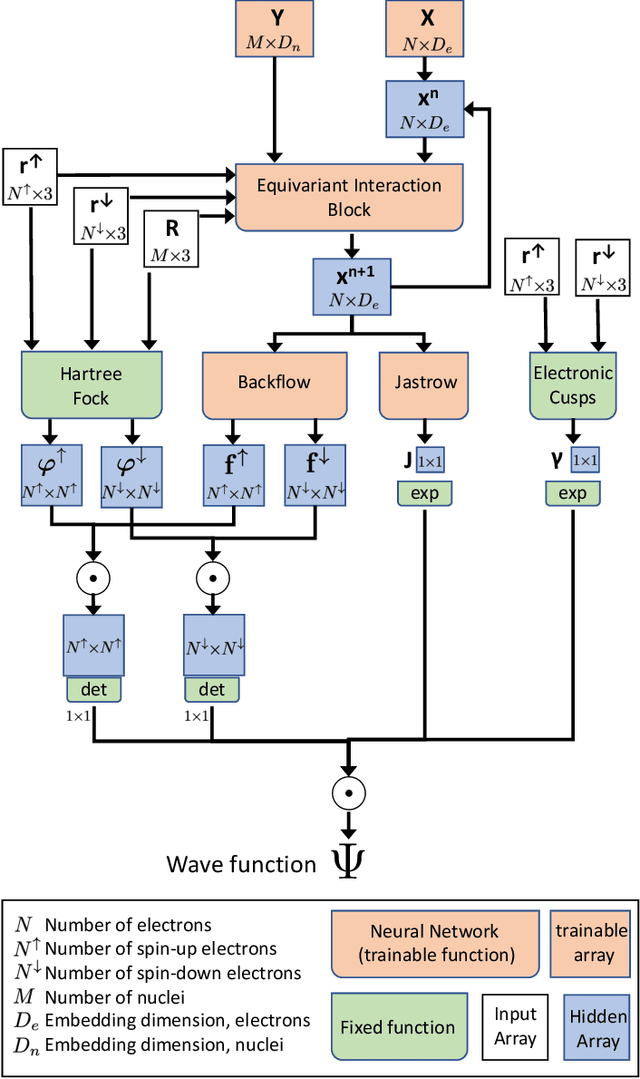
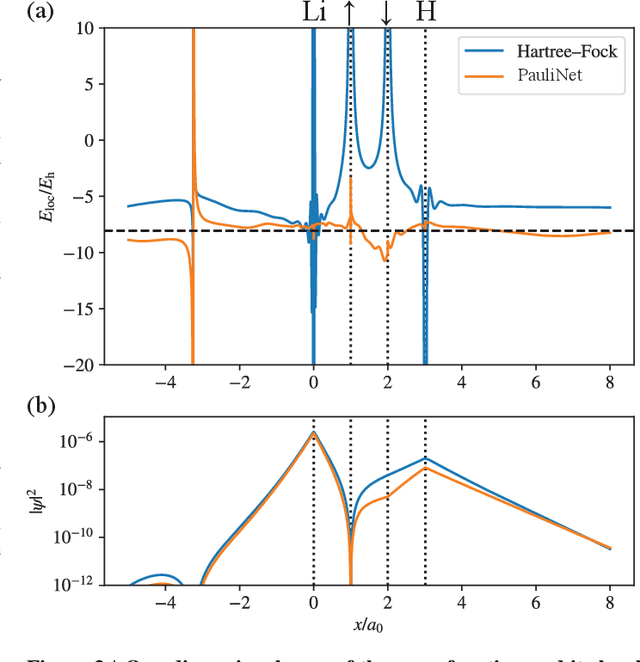
The electronic Schr\"odinger equation describes fundamental properties of molecules and materials, but cannot be solved exactly for larger systems than the hydrogen atom. Quantum Monte Carlo is a suitable method when high-quality approximations are sought, and its accuracy is in principle limited only by the flexibility of the used wave-function ansatz. Here we develop a deep-learning wave-function ansatz, dubbed PauliNet, which has the Hartree-Fock solution built in as a baseline, incorporates the physics of valid wave functions, and is trained using variational quantum Monte Carlo (VMC). Our deep-learning method achieves higher accuracy than comparable state-of-the-art VMC ansatzes for atoms, diatomic molecules and a strongly-correlated hydrogen chain. We anticipate that this method can reveal new physical insights and provide guidance for the design of molecules and materials where highly accurate quantum-mechanical solutions are needed, such as in transition metals and other strongly correlated systems.