Neural Wave Functions for Superfluids

Understanding superfluidity remains a major goal of condensed matter physics. Here we tackle this challenge utilizing the recently developed Fermionic neural network (FermiNet) wave function Ansatz for variational Monte Carlo calculations. We study the unitary Fermi gas, a system with strong, short-range, two-body interactions known to possess a superfluid ground state but difficult to describe quantitively. We demonstrate key limitations of the FermiNet Ansatz in studying the unitary Fermi gas and propose a simple modification that outperforms the original FermiNet significantly, giving highly accurate results. We prove mathematically that the new Ansatz is a strict generalization of the original FermiNet architecture, despite the use of fewer parameters. Our approach shares several advantanges with the FermiNet: the use of a neural network removes the need for an underlying basis set; and the flexiblity of the network yields extremely accurate results within a variational quantum Monte Carlo framework that provides access to unbiased estimates of arbitrary ground-state expectation values. We discuss how the method can be extended to study other superfluids.

Ab-initio quantum chemistry with neural-network wavefunctions

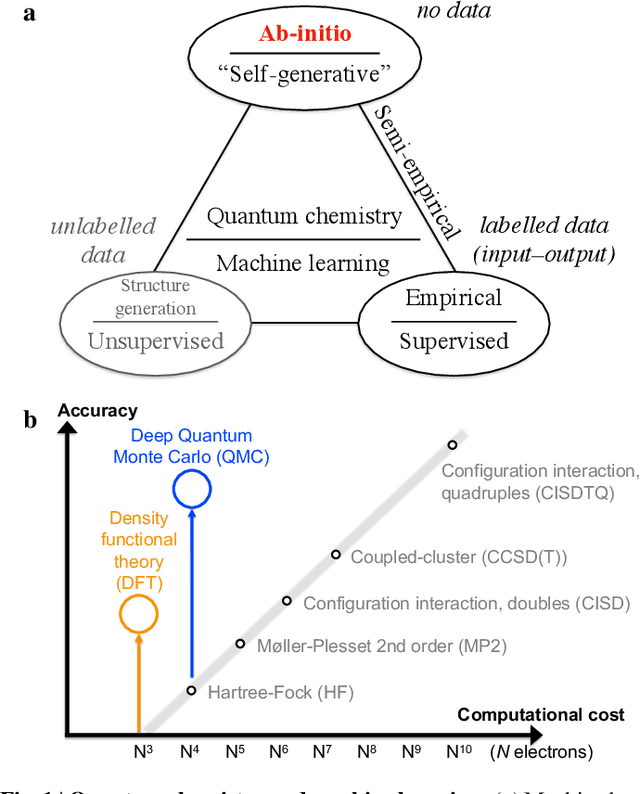
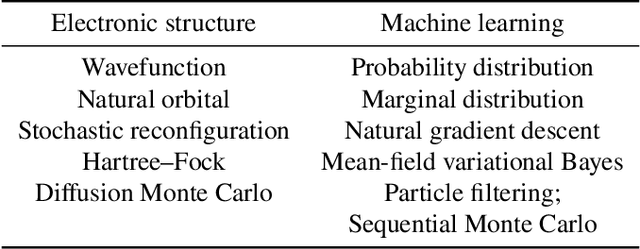
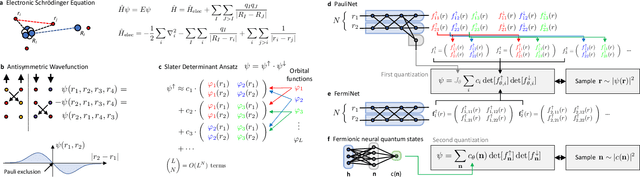
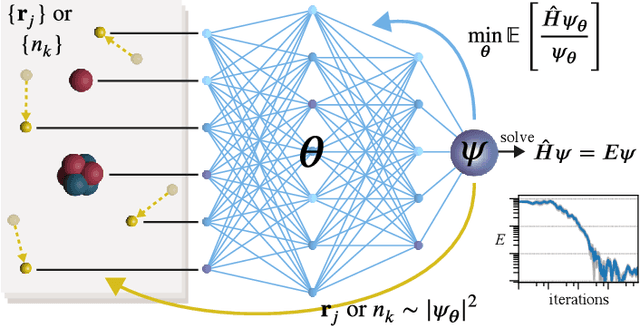
Machine learning and specifically deep-learning methods have outperformed human capabilities in many pattern recognition and data processing problems, in game playing, and now also play an increasingly important role in scientific discovery. A key application of machine learning in the molecular sciences is to learn potential energy surfaces or force fields from ab-initio solutions of the electronic Schr\"odinger equation using datasets obtained with density functional theory, coupled cluster, or other quantum chemistry methods. Here we review a recent and complementary approach: using machine learning to aid the direct solution of quantum chemistry problems from first principles. Specifically, we focus on quantum Monte Carlo (QMC) methods that use neural network ansatz functions in order to solve the electronic Schr\"odinger equation, both in first and second quantization, computing ground and excited states, and generalizing over multiple nuclear configurations. Compared to existing quantum chemistry methods, these new deep QMC methods have the potential to generate highly accurate solutions of the Schr\"odinger equation at relatively modest computational cost.

Discovering Quantum Phase Transitions with Fermionic Neural Networks

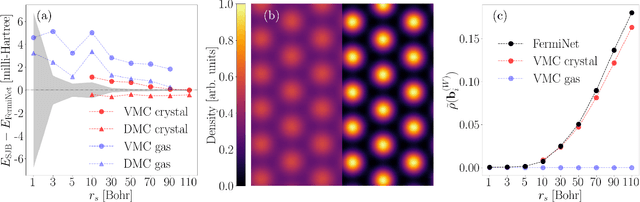
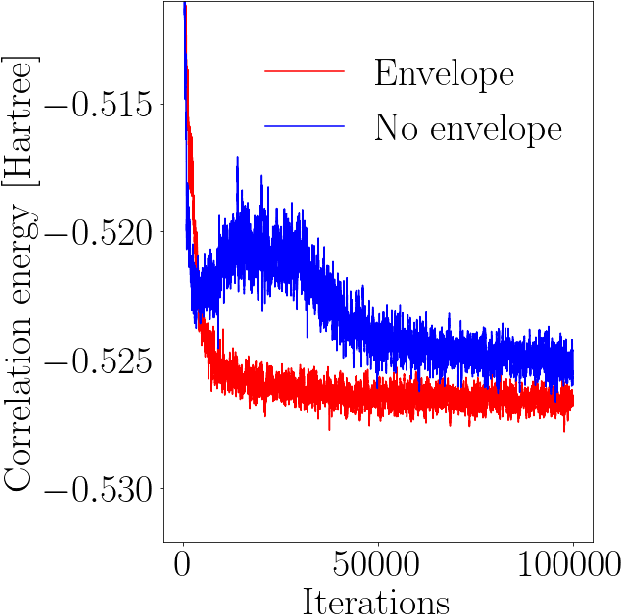
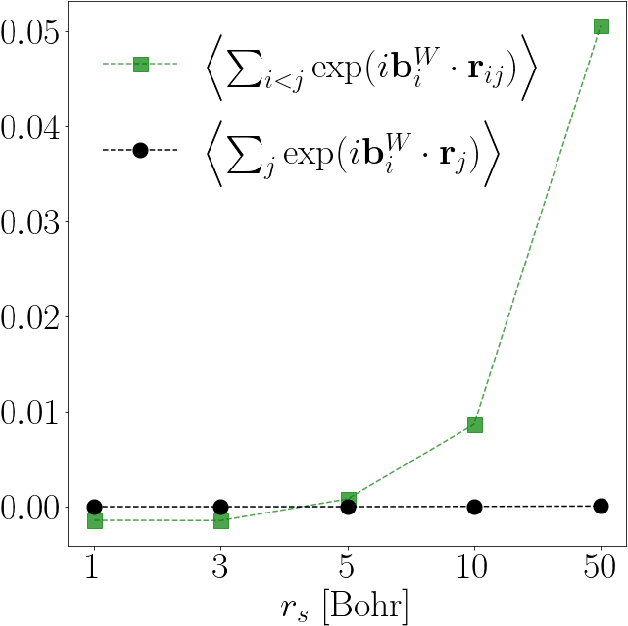
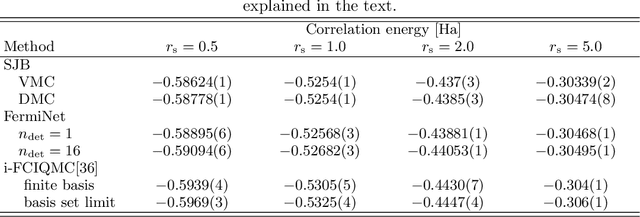
Deep neural networks have been extremely successful as highly accurate wave function ans\"atze for variational Monte Carlo calculations of molecular ground states. We present an extension of one such ansatz, FermiNet, to calculations of the ground states of periodic Hamiltonians, and study the homogeneous electron gas. FermiNet calculations of the ground-state energies of small electron gas systems are in excellent agreement with previous initiator full configuration interaction quantum Monte Carlo and diffusion Monte Carlo calculations. We investigate the spin-polarized homogeneous electron gas and demonstrate that the same neural network architecture is capable of accurately representing both the delocalized Fermi liquid state and the localized Wigner crystal state. The network is given no \emph{a priori} knowledge that a phase transition exists, but converges on the translationally invariant ground state at high density and spontaneously breaks the symmetry to produce the crystalline ground state at low density.

Better, Faster Fermionic Neural Networks

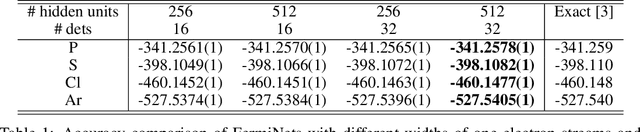
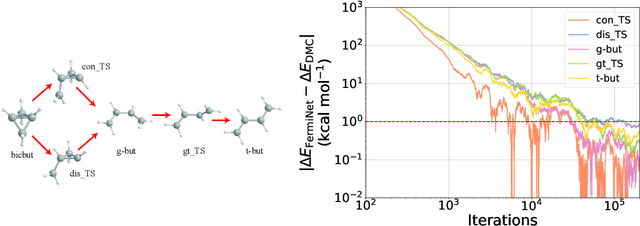
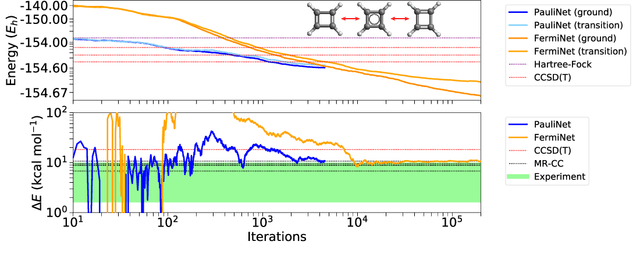
The Fermionic Neural Network (FermiNet) is a recently-developed neural network architecture that can be used as a wavefunction Ansatz for many-electron systems, and has already demonstrated high accuracy on small systems. Here we present several improvements to the FermiNet that allow us to set new records for speed and accuracy on challenging systems. We find that increasing the size of the network is sufficient to reach chemical accuracy on atoms as large as argon. Through a combination of implementing FermiNet in JAX and simplifying several parts of the network, we are able to reduce the number of GPU hours needed to train the FermiNet on large systems by an order of magnitude. This enables us to run the FermiNet on the challenging transition of bicyclobutane to butadiene and compare against the PauliNet on the automerization of cyclobutadiene, and we achieve results near the state of the art for both.

Ab-Initio Solution of the Many-Electron Schrödinger Equation with Deep Neural Networks

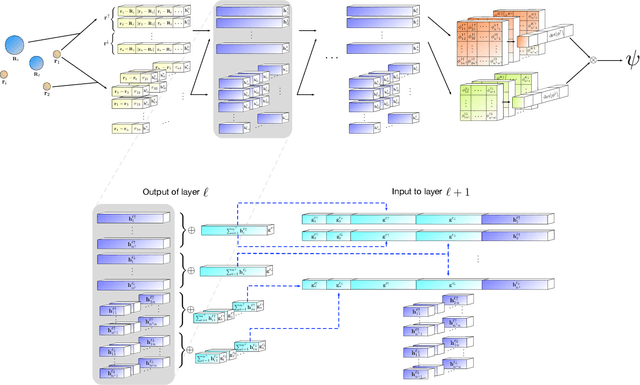
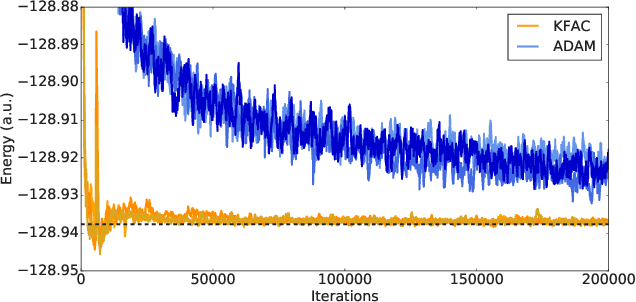
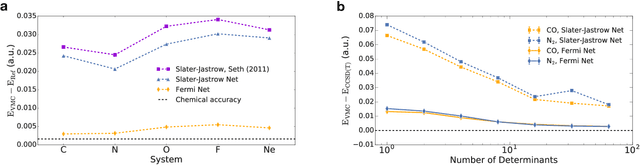
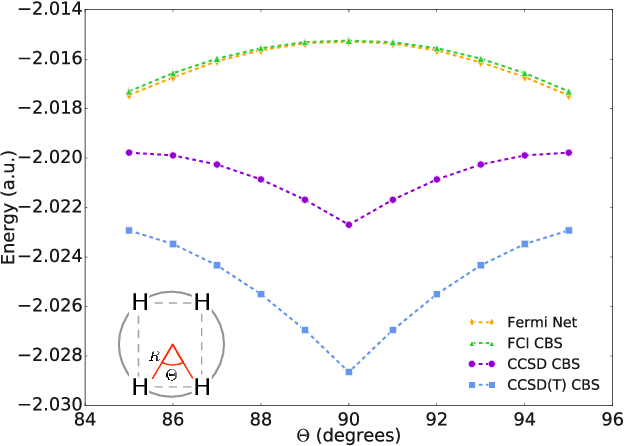
Given access to accurate solutions of the many-electron Schr\"odinger equation, nearly all chemistry could be derived from first principles. Exact wavefunctions of interesting chemical systems are out of reach because they are NP-hard to compute in general, but approximations can be found using polynomially-scaling algorithms. The key challenge for many of these algorithms is the choice of wavefunction approximation, or Ansatz, which must trade off between efficiency and accuracy. Neural networks have shown impressive power as accurate practical function approximators and promise as a compact wavefunction Ansatz for spin systems, but problems in electronic structure require wavefunctions that obey Fermi-Dirac statistics. Here we introduce a novel deep learning architecture, the Fermionic Neural Network, as a powerful wavefunction Ansatz for many-electron systems. The Fermionic Neural Network is able to achieve accuracy beyond other variational Monte Carlo Ans\"atze on a variety of atoms and small molecules. Using no data other than atomic positions and charges, we predict the dissociation curves of the nitrogen molecule and hydrogen chain, two challenging strongly-correlated systems, to significantly higher accuracy than the coupled cluster method, widely considered the gold standard for quantum chemistry. This demonstrates that deep neural networks can outperform existing ab-initio quantum chemistry methods, opening the possibility of accurate direct optimisation of wavefunctions for previously intractable molecules and solids.