Natural Quantum Monte Carlo Computation of Excited States

We present a variational Monte Carlo algorithm for estimating the lowest excited states of a quantum system which is a natural generalization of the estimation of ground states. The method has no free parameters and requires no explicit orthogonalization of the different states, instead transforming the problem of finding excited states of a given system into that of finding the ground state of an expanded system. Expected values of arbitrary observables can be calculated, including off-diagonal expectations between different states such as the transition dipole moment. Although the method is entirely general, it works particularly well in conjunction with recent work on using neural networks as variational Ansatze for many-electron systems, and we show that by combining this method with the FermiNet and Psiformer Ansatze we can accurately recover vertical excitation energies and oscillator strengths on molecules as large as benzene. Beyond the examples on molecules presented here, we expect this technique will be of great interest for applications of variational quantum Monte Carlo to atomic, nuclear and condensed matter physics.

A Self-Attention Ansatz for Ab-initio Quantum Chemistry

We present a novel neural network architecture using self-attention, the Wavefunction Transformer (Psiformer), which can be used as an approximation (or Ansatz) for solving the many-electron Schr\"odinger equation, the fundamental equation for quantum chemistry and material science. This equation can be solved from first principles, requiring no external training data. In recent years, deep neural networks like the FermiNet and PauliNet have been used to significantly improve the accuracy of these first-principle calculations, but they lack an attention-like mechanism for gating interactions between electrons. Here we show that the Psiformer can be used as a drop-in replacement for these other neural networks, often dramatically improving the accuracy of the calculations. On larger molecules especially, the ground state energy can be improved by dozens of kcal/mol, a qualitative leap over previous methods. This demonstrates that self-attention networks can learn complex quantum mechanical correlations between electrons, and are a promising route to reaching unprecedented accuracy in chemical calculations on larger systems.

Solving Mixed Integer Programs Using Neural Networks

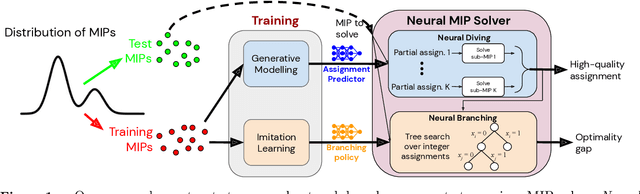
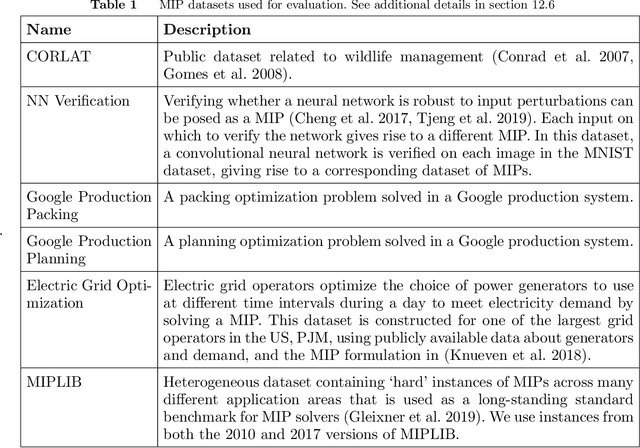
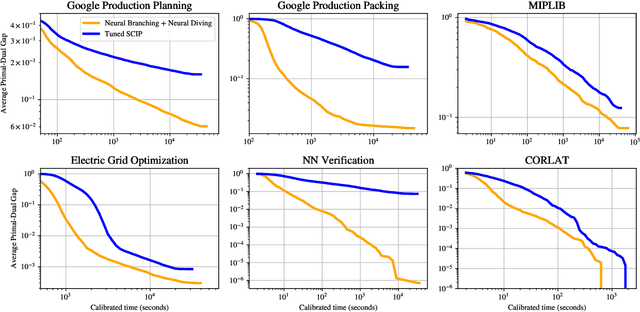
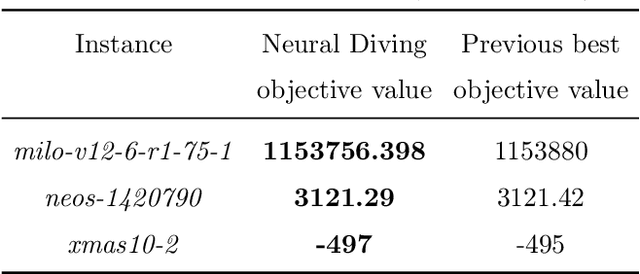
Mixed Integer Programming (MIP) solvers rely on an array of sophisticated heuristics developed with decades of research to solve large-scale MIP instances encountered in practice. Machine learning offers to automatically construct better heuristics from data by exploiting shared structure among instances in the data. This paper applies learning to the two key sub-tasks of a MIP solver, generating a high-quality joint variable assignment, and bounding the gap in objective value between that assignment and an optimal one. Our approach constructs two corresponding neural network-based components, Neural Diving and Neural Branching, to use in a base MIP solver such as SCIP. Neural Diving learns a deep neural network to generate multiple partial assignments for its integer variables, and the resulting smaller MIPs for un-assigned variables are solved with SCIP to construct high quality joint assignments. Neural Branching learns a deep neural network to make variable selection decisions in branch-and-bound to bound the objective value gap with a small tree. This is done by imitating a new variant of Full Strong Branching we propose that scales to large instances using GPUs. We evaluate our approach on six diverse real-world datasets, including two Google production datasets and MIPLIB, by training separate neural networks on each. Most instances in all the datasets combined have $10^3-10^6$ variables and constraints after presolve, which is significantly larger than previous learning approaches. Comparing solvers with respect to primal-dual gap averaged over a held-out set of instances, the learning-augmented SCIP is 2x to 10x better on all datasets except one on which it is $10^5$x better, at large time limits. To the best of our knowledge, ours is the first learning approach to demonstrate such large improvements over SCIP on both large-scale real-world application datasets and MIPLIB.