Ab-initio quantum chemistry with neural-network wavefunctions

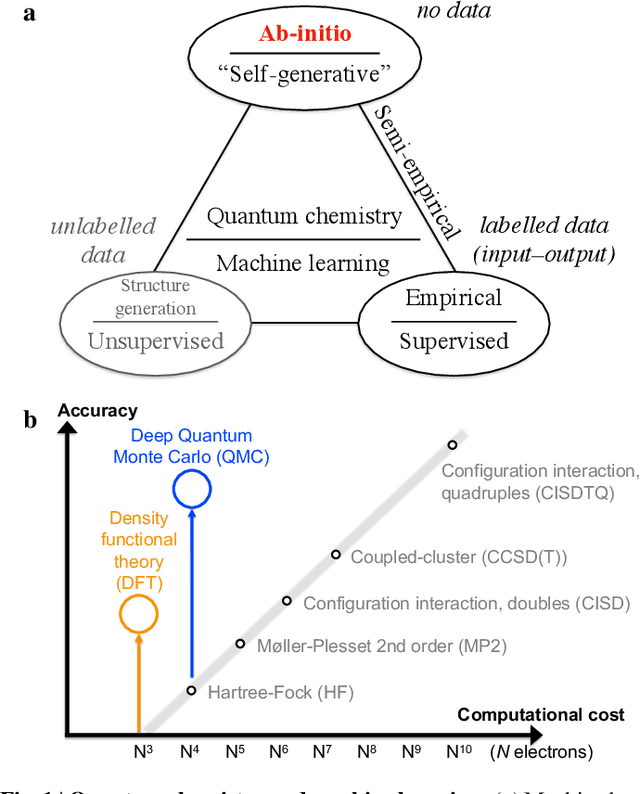
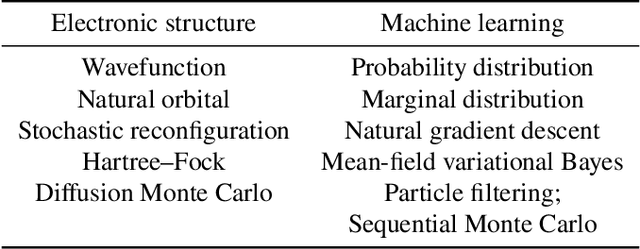
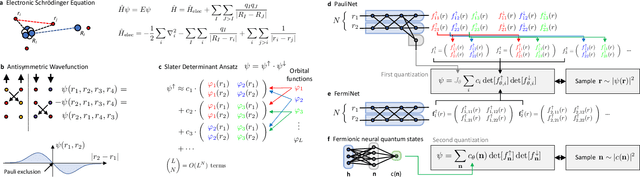
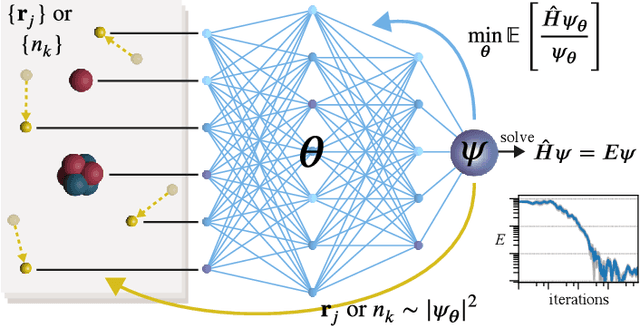
Machine learning and specifically deep-learning methods have outperformed human capabilities in many pattern recognition and data processing problems, in game playing, and now also play an increasingly important role in scientific discovery. A key application of machine learning in the molecular sciences is to learn potential energy surfaces or force fields from ab-initio solutions of the electronic Schr\"odinger equation using datasets obtained with density functional theory, coupled cluster, or other quantum chemistry methods. Here we review a recent and complementary approach: using machine learning to aid the direct solution of quantum chemistry problems from first principles. Specifically, we focus on quantum Monte Carlo (QMC) methods that use neural network ansatz functions in order to solve the electronic Schr\"odinger equation, both in first and second quantization, computing ground and excited states, and generalizing over multiple nuclear configurations. Compared to existing quantum chemistry methods, these new deep QMC methods have the potential to generate highly accurate solutions of the Schr\"odinger equation at relatively modest computational cost.

An analytic theory for the dynamics of wide quantum neural networks

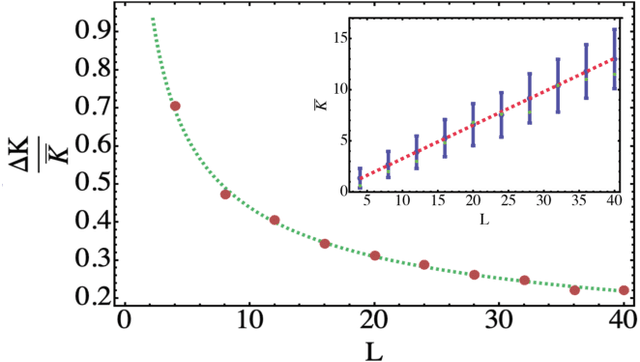
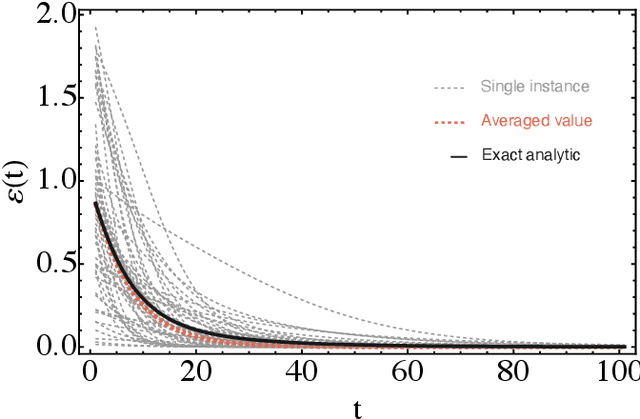
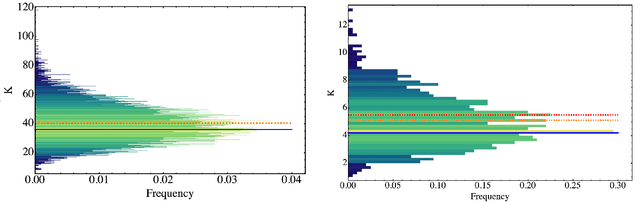
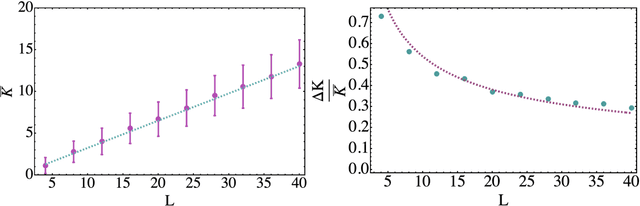
Parametrized quantum circuits can be used as quantum neural networks and have the potential to outperform their classical counterparts when trained for addressing learning problems. To date, much of the results on their performance on practical problems are heuristic in nature. In particular, the convergence rate for the training of quantum neural networks is not fully understood. Here, we analyze the dynamics of gradient descent for the training error of a class of variational quantum machine learning models. We define wide quantum neural networks as parameterized quantum circuits in the limit of a large number of qubits and variational parameters. We then find a simple analytic formula that captures the average behavior of their loss function and discuss the consequences of our findings. For example, for random quantum circuits, we predict and characterize an exponential decay of the residual training error as a function of the parameters of the system. We finally validate our analytic results with numerical experiments.

Representation Learning via Quantum Neural Tangent Kernels

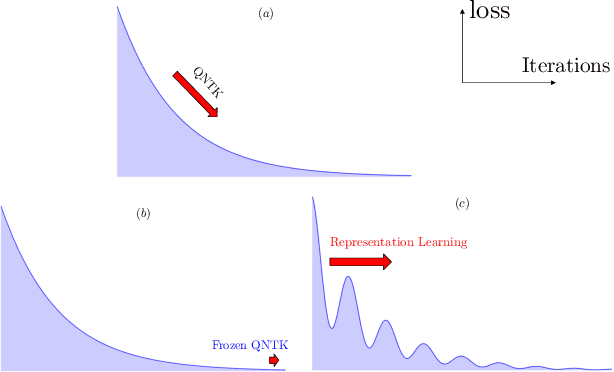
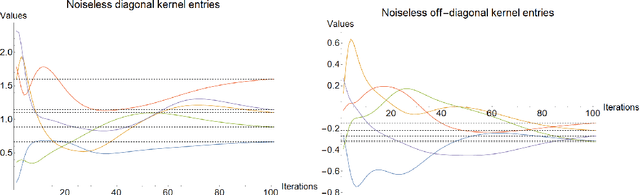
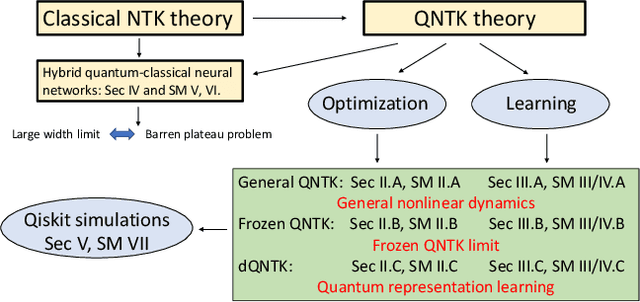
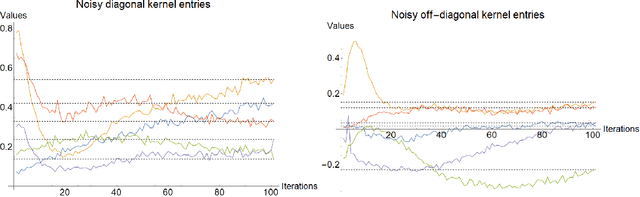
Variational quantum circuits are used in quantum machine learning and variational quantum simulation tasks. Designing good variational circuits or predicting how well they perform for given learning or optimization tasks is still unclear. Here we discuss these problems, analyzing variational quantum circuits using the theory of neural tangent kernels. We define quantum neural tangent kernels, and derive dynamical equations for their associated loss function in optimization and learning tasks. We analytically solve the dynamics in the frozen limit, or lazy training regime, where variational angles change slowly and a linear perturbation is good enough. We extend the analysis to a dynamical setting, including quadratic corrections in the variational angles. We then consider hybrid quantum-classical architecture and define a large-width limit for hybrid kernels, showing that a hybrid quantum-classical neural network can be approximately Gaussian. The results presented here show limits for which analytical understandings of the training dynamics for variational quantum circuits, used for quantum machine learning and optimization problems, are possible. These analytical results are supported by numerical simulations of quantum machine learning experiments.