A Survey of Deep Learning-based Point Cloud Denoising

Accurate 3D geometry acquisition is essential for a wide range of applications, such as computer graphics, autonomous driving, robotics, and augmented reality. However, raw point clouds acquired in real-world environments are often corrupted with noise due to various factors such as sensor, lighting, material, environment etc, which reduces geometric fidelity and degrades downstream performance. Point cloud denoising is a fundamental problem, aiming to recover clean point sets while preserving underlying structures. Classical optimization-based methods, guided by hand-crafted filters or geometric priors, have been extensively studied but struggle to handle diverse and complex noise patterns. Recent deep learning approaches leverage neural network architectures to learn distinctive representations and demonstrate strong outcomes, particularly on complex and large-scale point clouds. Provided these significant advances, this survey provides a comprehensive and up-to-date review of deep learning-based point cloud denoising methods up to August 2025. We organize the literature from two perspectives: (1) supervision level (supervised vs. unsupervised), and (2) modeling perspective, proposing a functional taxonomy that unifies diverse approaches by their denoising principles. We further analyze architectural trends both structurally and chronologically, establish a unified benchmark with consistent training settings, and evaluate methods in terms of denoising quality, surface fidelity, point distribution, and computational efficiency. Finally, we discuss open challenges and outline directions for future research in this rapidly evolving field.

Hybrid Long and Short Range Flows for Point Cloud Filtering

Point cloud capture processes are error-prone and introduce noisy artifacts that necessitate filtering/denoising. Recent filtering methods often suffer from point clustering or noise retaining issues. In this paper, we propose Hybrid Point Cloud Filtering ($\textbf{HybridPF}$) that considers both short-range and long-range filtering trajectories when removing noise. It is well established that short range scores, given by $\nabla_{x}\log p(x_t)$, may provide the necessary displacements to move noisy points to the underlying clean surface. By contrast, long range velocity flows approximate constant displacements directed from a high noise variant patch $x_0$ towards the corresponding clean surface $x_1$. Here, noisy patches $x_t$ are viewed as intermediate states between the high noise variant and the clean patches. Our intuition is that long range information from velocity flow models can guide the short range scores to align more closely with the clean points. In turn, score models generally provide a quicker convergence to the clean surface. Specifically, we devise two parallel modules, the ShortModule and LongModule, each consisting of an Encoder-Decoder pair to respectively account for short-range scores and long-range flows. We find that short-range scores, guided by long-range features, yield filtered point clouds with good point distributions and convergence near the clean surface. We design a joint loss function to simultaneously train the ShortModule and LongModule, in an end-to-end manner. Finally, we identify a key weakness in current displacement based methods, limitations on the decoder architecture, and propose a dynamic graph convolutional decoder to improve the inference process. Comprehensive experiments demonstrate that our HybridPF achieves state-of-the-art results while enabling faster inference speed.

StraightPCF: Straight Point Cloud Filtering

Point cloud filtering is a fundamental 3D vision task, which aims to remove noise while recovering the underlying clean surfaces. State-of-the-art methods remove noise by moving noisy points along stochastic trajectories to the clean surfaces. These methods often require regularization within the training objective and/or during post-processing, to ensure fidelity. In this paper, we introduce StraightPCF, a new deep learning based method for point cloud filtering. It works by moving noisy points along straight paths, thus reducing discretization errors while ensuring faster convergence to the clean surfaces. We model noisy patches as intermediate states between high noise patch variants and their clean counterparts, and design the VelocityModule to infer a constant flow velocity from the former to the latter. This constant flow leads to straight filtering trajectories. In addition, we introduce a DistanceModule that scales the straight trajectory using an estimated distance scalar to attain convergence near the clean surface. Our network is lightweight and only has $\sim530K$ parameters, being 17% of IterativePFN (a most recent point cloud filtering network). Extensive experiments on both synthetic and real-world data show our method achieves state-of-the-art results. Our method also demonstrates nice distributions of filtered points without the need for regularization. The implementation code can be found at: https://github.com/ddsediri/StraightPCF.

IterativePFN: True Iterative Point Cloud Filtering

The quality of point clouds is often limited by noise introduced during their capture process. Consequently, a fundamental 3D vision task is the removal of noise, known as point cloud filtering or denoising. State-of-the-art learning based methods focus on training neural networks to infer filtered displacements and directly shift noisy points onto the underlying clean surfaces. In high noise conditions, they iterate the filtering process. However, this iterative filtering is only done at test time and is less effective at ensuring points converge quickly onto the clean surfaces. We propose IterativePFN (iterative point cloud filtering network), which consists of multiple IterationModules that model the true iterative filtering process internally, within a single network. We train our IterativePFN network using a novel loss function that utilizes an adaptive ground truth target at each iteration to capture the relationship between intermediate filtering results during training. This ensures that the filtered results converge faster to the clean surfaces. Our method is able to obtain better performance compared to state-of-the-art methods. The source code can be found at: https://github.com/ddsediri/IterativePFN.

Contrastive Learning for Joint Normal Estimation and Point Cloud Filtering

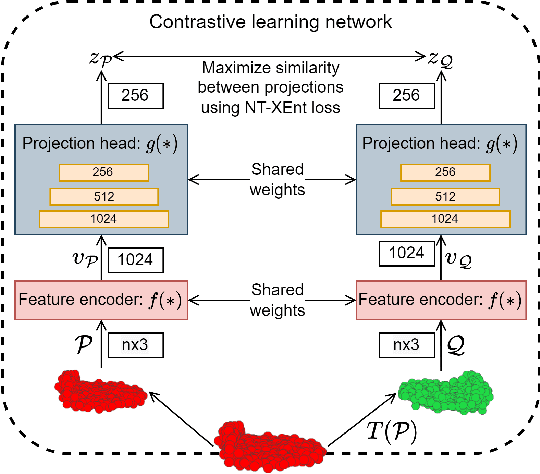
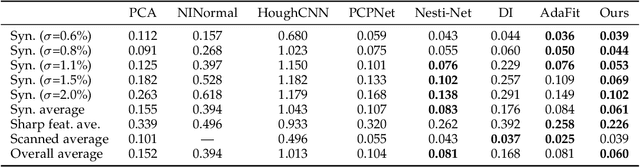
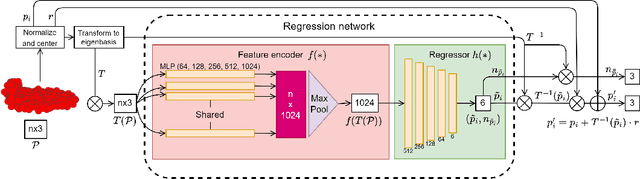
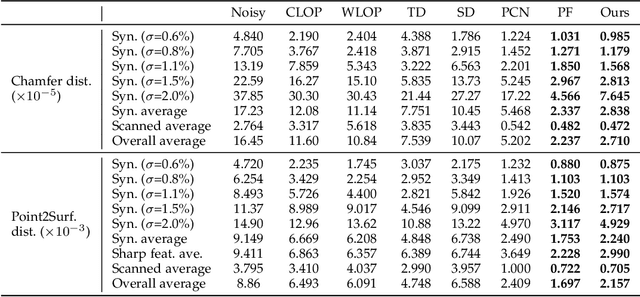
Point cloud filtering and normal estimation are two fundamental research problems in the 3D field. Existing methods usually perform normal estimation and filtering separately and often show sensitivity to noise and/or inability to preserve sharp geometric features such as corners and edges. In this paper, we propose a novel deep learning method to jointly estimate normals and filter point clouds. We first introduce a 3D patch based contrastive learning framework, with noise corruption as an augmentation, to train a feature encoder capable of generating faithful representations of point cloud patches while remaining robust to noise. These representations are consumed by a simple regression network and supervised by a novel joint loss, simultaneously estimating point normals and displacements that are used to filter the patch centers. Experimental results show that our method well supports the two tasks simultaneously and preserves sharp features and fine details. It generally outperforms state-of-the-art techniques on both tasks.

Deep Point Cloud Normal Estimation via Triplet Learning

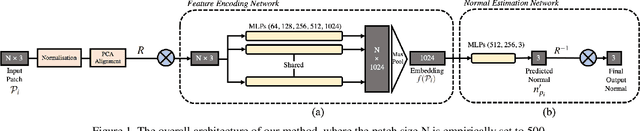
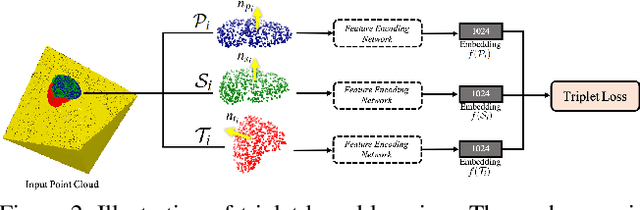
Normal estimation on 3D point clouds is a fundamental problem in 3D vision and graphics. Current methods often show limited accuracy in predicting normals at sharp features (e.g., edges and corners) and less robustness to noise. In this paper, we propose a novel normal estimation method for point clouds. It consists of two phases: (a) feature encoding which learns representations of local patches, and (b) normal estimation that takes the learned representation as input and regresses the normal vector. We are motivated that local patches on isotropic and anisotropic surfaces have similar or distinct normals, and that separable features or representations can be learned to facilitate normal estimation. To realise this, we first construct triplets of local patches on 3D point cloud data, and design a triplet network with a triplet loss for feature encoding. We then design a simple network with several MLPs and a loss function to regress the normal vector. Despite having a smaller network size compared to most other methods, experimental results show that our method preserves sharp features and achieves better normal estimation results on CAD-like shapes.