Neural Active Learning on Heteroskedastic Distributions

Models that can actively seek out the best quality training data hold the promise of more accurate, adaptable, and efficient machine learning. State-of-the-art active learning techniques tend to prefer examples that are the most difficult to classify. While this works well on homogeneous datasets, we find that it can lead to catastrophic failures when performed on multiple distributions with different degrees of label noise or heteroskedasticity. These active learning algorithms strongly prefer to draw from the distribution with more noise, even if their examples have no informative structure (such as solid color images with random labels). To this end, we demonstrate the catastrophic failure of these active learning algorithms on heteroskedastic distributions and propose a fine-tuning-based approach to mitigate these failures. Further, we propose a new algorithm that incorporates a model difference scoring function for each data point to filter out the noisy examples and sample clean examples that maximize accuracy, outperforming the existing active learning techniques on the heteroskedastic datasets. We hope these observations and techniques are immediately helpful to practitioners and can help to challenge common assumptions in the design of active learning algorithms.

Transformers Learn Shortcuts to Automata

Algorithmic reasoning requires capabilities which are most naturally understood through recurrent models of computation, like the Turing machine. However, Transformer models, while lacking recurrence, are able to perform such reasoning using far fewer layers than the number of reasoning steps. This raises the question: what solutions are these shallow and non-recurrent models finding? We investigate this question in the setting of learning automata, discrete dynamical systems naturally suited to recurrent modeling and expressing algorithmic tasks. Our theoretical results completely characterize shortcut solutions, whereby a shallow Transformer with only $o(T)$ layers can exactly replicate the computation of an automaton on an input sequence of length $T$. By representing automata using the algebraic structure of their underlying transformation semigroups, we obtain $O(\log T)$-depth simulators for all automata and $O(1)$-depth simulators for all automata whose associated groups are solvable. Empirically, we perform synthetic experiments by training Transformers to simulate a wide variety of automata, and show that shortcut solutions can be learned via standard training. We further investigate the brittleness of these solutions and propose potential mitigations.

Recurrent Convolutional Neural Networks Learn Succinct Learning Algorithms

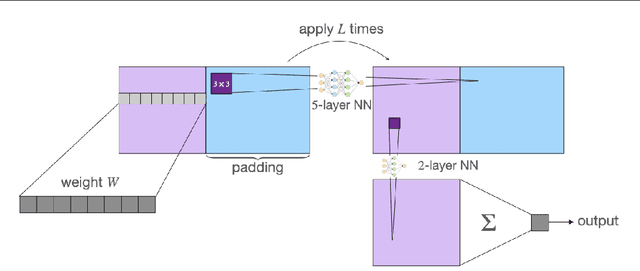
Neural Networks (NNs) struggle to efficiently learn certain problems, such as parity problems, even when there are simple learning algorithms for those problems. Can NNs discover learning algorithms on their own? We exhibit a NN architecture that, in polynomial time, learns as well as any efficient learning algorithm describable by a constant-sized learning algorithm. For example, on parity problems, the NN learns as well as row reduction, an efficient algorithm that can be succinctly described. Our architecture combines both recurrent weight-sharing between layers and convolutional weight-sharing to reduce the number of parameters down to a constant, even though the network itself may have trillions of nodes. While in practice the constants in our analysis are too large to be directly meaningful, our work suggests that the synergy of Recurrent and Convolutional NNs (RCNNs) may be more powerful than either alone.

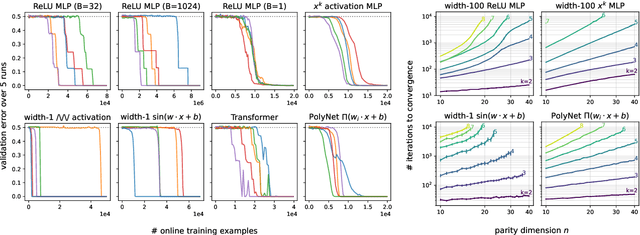
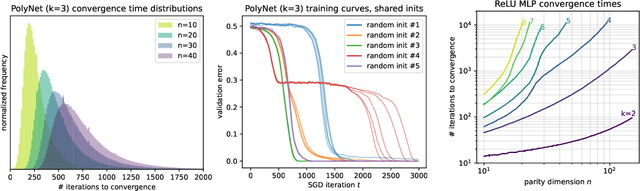
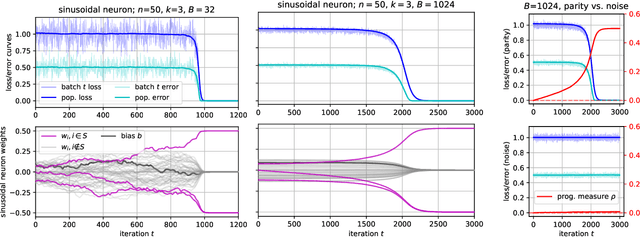
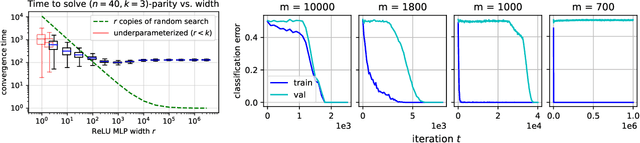
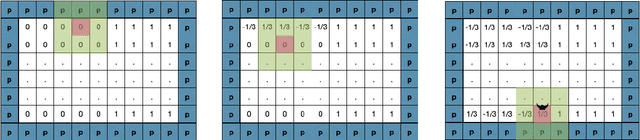
Hidden Progress in Deep Learning: SGD Learns Parities Near the Computational Limit

There is mounting empirical evidence of emergent phenomena in the capabilities of deep learning methods as we scale up datasets, model sizes, and training times. While there are some accounts of how these resources modulate statistical capacity, far less is known about their effect on the computational problem of model training. This work conducts such an exploration through the lens of learning $k$-sparse parities of $n$ bits, a canonical family of problems which pose theoretical computational barriers. In this setting, we find that neural networks exhibit surprising phase transitions when scaling up dataset size and running time. In particular, we demonstrate empirically that with standard training, a variety of architectures learn sparse parities with $n^{O(k)}$ examples, with loss (and error) curves abruptly dropping after $n^{O(k)}$ iterations. These positive results nearly match known SQ lower bounds, even without an explicit sparsity-promoting prior. We elucidate the mechanisms of these phenomena with a theoretical analysis: we find that the phase transition in performance is not due to SGD "stumbling in the dark" until it finds the hidden set of features (a natural algorithm which also runs in $n^{O(k)}$ time); instead, we show that SGD gradually amplifies a Fourier gap in the population gradient.

Understanding Contrastive Learning Requires Incorporating Inductive Biases

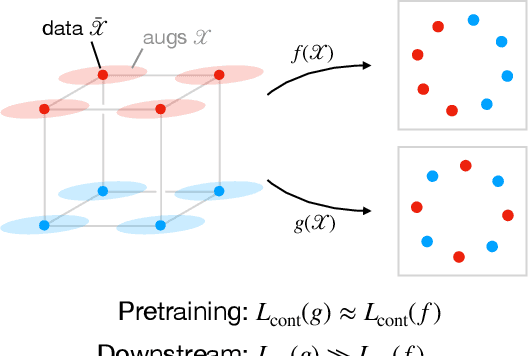
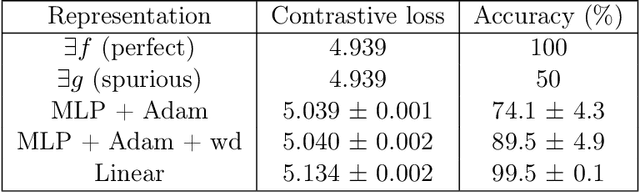
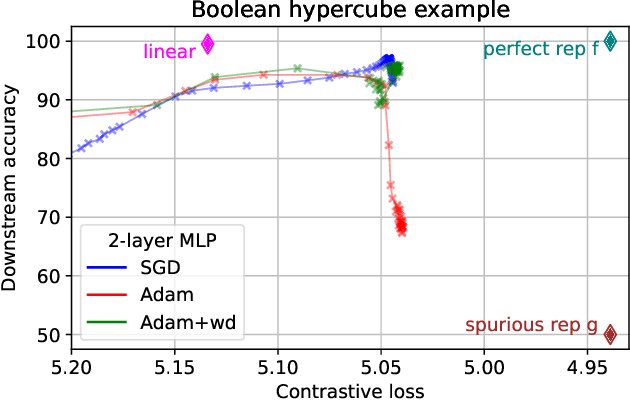
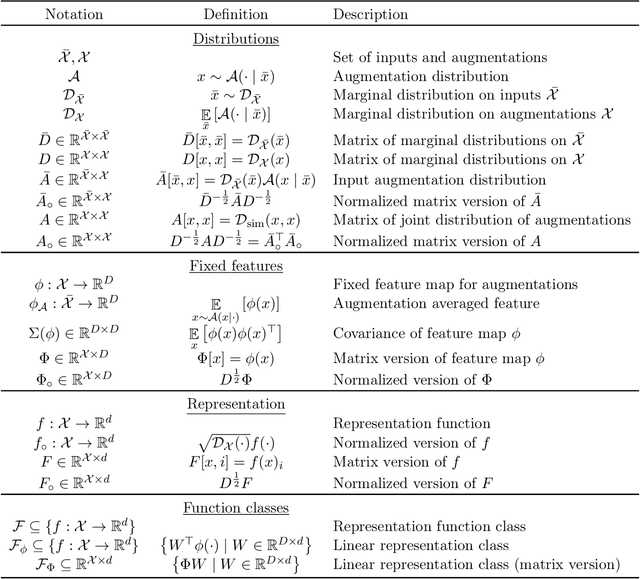
Contrastive learning is a popular form of self-supervised learning that encourages augmentations (views) of the same input to have more similar representations compared to augmentations of different inputs. Recent attempts to theoretically explain the success of contrastive learning on downstream classification tasks prove guarantees depending on properties of {\em augmentations} and the value of {\em contrastive loss} of representations. We demonstrate that such analyses, that ignore {\em inductive biases} of the function class and training algorithm, cannot adequately explain the success of contrastive learning, even {\em provably} leading to vacuous guarantees in some settings. Extensive experiments on image and text domains highlight the ubiquity of this problem -- different function classes and algorithms behave very differently on downstream tasks, despite having the same augmentations and contrastive losses. Theoretical analysis is presented for the class of linear representations, where incorporating inductive biases of the function class allows contrastive learning to work with less stringent conditions compared to prior analyses.

Machine Learning for Mechanical Ventilation Control (Extended Abstract)

Mechanical ventilation is one of the most widely used therapies in the ICU. However, despite broad application from anaesthesia to COVID-related life support, many injurious challenges remain. We frame these as a control problem: ventilators must let air in and out of the patient's lungs according to a prescribed trajectory of airway pressure. Industry-standard controllers, based on the PID method, are neither optimal nor robust. Our data-driven approach learns to control an invasive ventilator by training on a simulator itself trained on data collected from the ventilator. This method outperforms popular reinforcement learning algorithms and even controls the physical ventilator more accurately and robustly than PID. These results underscore how effective data-driven methodologies can be for invasive ventilation and suggest that more general forms of ventilation (e.g., non-invasive, adaptive) may also be amenable.

Anti-Concentrated Confidence Bonuses for Scalable Exploration

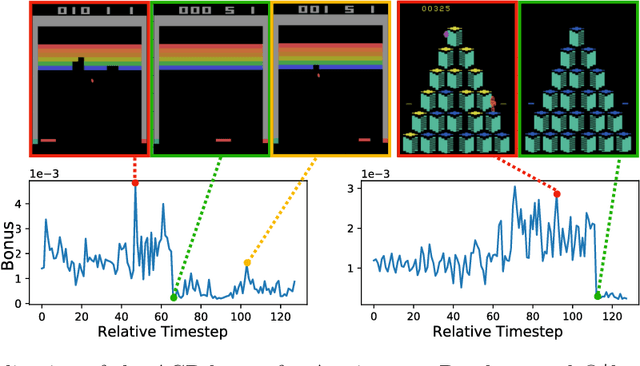
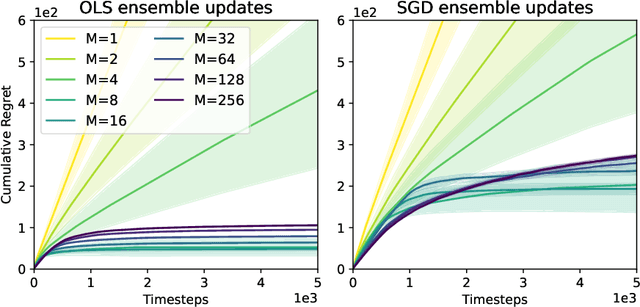
Intrinsic rewards play a central role in handling the exploration-exploitation trade-off when designing sequential decision-making algorithms, in both foundational theory and state-of-the-art deep reinforcement learning. The LinUCB algorithm, a centerpiece of the stochastic linear bandits literature, prescribes an elliptical bonus which addresses the challenge of leveraging shared information in large action spaces. This bonus scheme cannot be directly transferred to high-dimensional exploration problems, however, due to the computational cost of maintaining the inverse covariance matrix of action features. We introduce \emph{anti-concentrated confidence bounds} for efficiently approximating the elliptical bonus, using an ensemble of regressors trained to predict random noise from policy network-derived features. Using this approximation, we obtain stochastic linear bandit algorithms which obtain $\tilde O(d \sqrt{T})$ regret bounds for $\mathrm{poly}(d)$ fixed actions. We develop a practical variant for deep reinforcement learning that is competitive with contemporary intrinsic reward heuristics on Atari benchmarks.

Inductive Biases and Variable Creation in Self-Attention Mechanisms

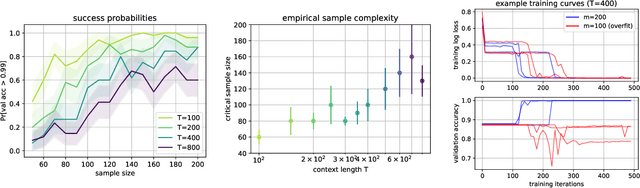
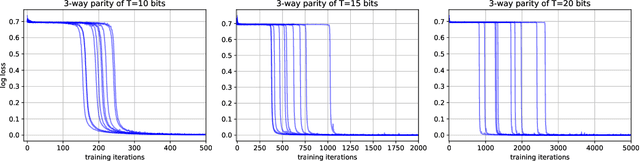
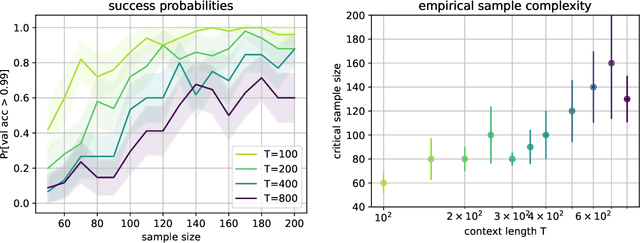
Self-attention, an architectural motif designed to model long-range interactions in sequential data, has driven numerous recent breakthroughs in natural language processing and beyond. This work provides a theoretical analysis of the inductive biases of self-attention modules, where our focus is to rigorously establish which functions and long-range dependencies self-attention blocks prefer to represent. Our main result shows that bounded-norm Transformer layers create sparse variables: they can represent sparse functions of the input sequence, with sample complexity scaling only logarithmically with the context length. Furthermore, we propose new experimental protocols to support this analysis and to guide the practice of training Transformers, built around the large body of work on provably learning sparse Boolean functions.

Sparsity in Partially Controllable Linear Systems

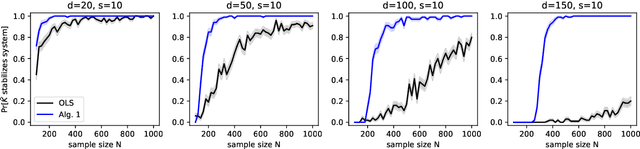
A fundamental concept in control theory is that of controllability, where any system state can be reached through an appropriate choice of control inputs. Indeed, a large body of classical and modern approaches are designed for controllable linear dynamical systems. However, in practice, we often encounter systems in which a large set of state variables evolve exogenously and independently of the control inputs; such systems are only \emph{partially controllable}. The focus of this work is on a large class of partially controllable linear dynamical systems, specified by an underlying sparsity pattern. Our main results establish structural conditions and finite-sample guarantees for learning to control such systems. In particular, our structural results characterize those state variables which are irrelevant for optimal control, an analysis which departs from classical control techniques. Our algorithmic results adapt techniques from high-dimensional statistics -- specifically soft-thresholding and semiparametric least-squares -- to exploit the underlying sparsity pattern in order to obtain finite-sample guarantees that significantly improve over those based on certainty-equivalence. We also corroborate these theoretical improvements over certainty-equivalent control through a simulation study.

Acceleration via Fractal Learning Rate Schedules

When balancing the practical tradeoffs of iterative methods for large-scale optimization, the learning rate schedule remains notoriously difficult to understand and expensive to tune. We demonstrate the presence of these subtleties even in the innocuous case when the objective is a convex quadratic. We reinterpret an iterative algorithm from the numerical analysis literature as what we call the Chebyshev learning rate schedule for accelerating vanilla gradient descent, and show that the problem of mitigating instability leads to a fractal ordering of step sizes. We provide some experiments and discussion to challenge current understandings of the "edge of stability" in deep learning: even in simple settings, provable acceleration can be obtained by making negative local progress on the objective.