Agnostic Active Learning of Single Index Models with Linear Sample Complexity

We study active learning methods for single index models of the form $F({\mathbf x}) = f(\langle {\mathbf w}, {\mathbf x}\rangle)$, where $f:\mathbb{R} \to \mathbb{R}$ and ${\mathbf x,\mathbf w} \in \mathbb{R}^d$. In addition to their theoretical interest as simple examples of non-linear neural networks, single index models have received significant recent attention due to applications in scientific machine learning like surrogate modeling for partial differential equations (PDEs). Such applications require sample-efficient active learning methods that are robust to adversarial noise. I.e., that work even in the challenging agnostic learning setting. We provide two main results on agnostic active learning of single index models. First, when $f$ is known and Lipschitz, we show that $\tilde{O}(d)$ samples collected via {statistical leverage score sampling} are sufficient to learn a near-optimal single index model. Leverage score sampling is simple to implement, efficient, and already widely used for actively learning linear models. Our result requires no assumptions on the data distribution, is optimal up to log factors, and improves quadratically on a recent ${O}(d^{2})$ bound of \cite{gajjar2023active}. Second, we show that $\tilde{O}(d)$ samples suffice even in the more difficult setting when $f$ is \emph{unknown}. Our results leverage tools from high dimensional probability, including Dudley's inequality and dual Sudakov minoration, as well as a novel, distribution-aware discretization of the class of Lipschitz functions.

Faster Linear Systems and Matrix Norm Approximation via Multi-level Sketched Preconditioning

We present a new class of preconditioned iterative methods for solving linear systems of the form $Ax = b$. Our methods are based on constructing a low-rank Nystr\"om approximation to $A$ using sparse random sketching. This approximation is used to construct a preconditioner, which itself is inverted quickly using additional levels of random sketching and preconditioning. We prove that the convergence of our methods depends on a natural average condition number of $A$, which improves as the rank of the Nystr\"om approximation increases. Concretely, this allows us to obtain faster runtimes for a number of fundamental linear algebraic problems: 1. We show how to solve any $n\times n$ linear system that is well-conditioned except for $k$ outlying large singular values in $\tilde{O}(n^{2.065} + k^\omega)$ time, improving on a recent result of [Derezi\'nski, Yang, STOC 2024] for all $k \gtrsim n^{0.78}$. 2. We give the first $\tilde{O}(n^2 + {d_\lambda}^{\omega}$) time algorithm for solving a regularized linear system $(A + \lambda I)x = b$, where $A$ is positive semidefinite with effective dimension $d_\lambda$. This problem arises in applications like Gaussian process regression. 3. We give faster algorithms for approximating Schatten $p$-norms and other matrix norms. For example, for the Schatten 1 (nuclear) norm, we give an algorithm that runs in $\tilde{O}(n^{2.11})$ time, improving on an $\tilde{O}(n^{2.18})$ method of [Musco et al., ITCS 2018]. Interestingly, previous state-of-the-art algorithms for most of the problems above relied on stochastic iterative methods, like stochastic coordinate and gradient descent. Our work takes a completely different approach, instead leveraging tools from matrix sketching.

A Simple and Practical Method for Reducing the Disparate Impact of Differential Privacy

Differentially private (DP) mechanisms have been deployed in a variety of high-impact social settings (perhaps most notably by the U.S. Census). Since all DP mechanisms involve adding noise to results of statistical queries, they are expected to impact our ability to accurately analyze and learn from data, in effect trading off privacy with utility. Alarmingly, the impact of DP on utility can vary significantly among different sub-populations. A simple way to reduce this disparity is with stratification. First compute an independent private estimate for each group in the data set (which may be the intersection of several protected classes), then, to compute estimates of global statistics, appropriately recombine these group estimates. Our main observation is that naive stratification often yields high-accuracy estimates of population-level statistics, without the need for additional privacy budget. We support this observation theoretically and empirically. Our theoretical results center on the private mean estimation problem, while our empirical results center on extensive experiments on private data synthesis to demonstrate the effectiveness of stratification on a variety of private mechanisms. Overall, we argue that this straightforward approach provides a strong baseline against which future work on reducing utility disparities of DP mechanisms should be compared.

Structured Semidefinite Programming for Recovering Structured Preconditioners

We develop a general framework for finding approximately-optimal preconditioners for solving linear systems. Leveraging this framework we obtain improved runtimes for fundamental preconditioning and linear system solving problems including the following. We give an algorithm which, given positive definite $\mathbf{K} \in \mathbb{R}^{d \times d}$ with $\mathrm{nnz}(\mathbf{K})$ nonzero entries, computes an $\epsilon$-optimal diagonal preconditioner in time $\widetilde{O}(\mathrm{nnz}(\mathbf{K}) \cdot \mathrm{poly}(\kappa^\star,\epsilon^{-1}))$, where $\kappa^\star$ is the optimal condition number of the rescaled matrix. We give an algorithm which, given $\mathbf{M} \in \mathbb{R}^{d \times d}$ that is either the pseudoinverse of a graph Laplacian matrix or a constant spectral approximation of one, solves linear systems in $\mathbf{M}$ in $\widetilde{O}(d^2)$ time. Our diagonal preconditioning results improve state-of-the-art runtimes of $\Omega(d^{3.5})$ attained by general-purpose semidefinite programming, and our solvers improve state-of-the-art runtimes of $\Omega(d^{\omega})$ where $\omega > 2.3$ is the current matrix multiplication constant. We attain our results via new algorithms for a class of semidefinite programs (SDPs) we call matrix-dictionary approximation SDPs, which we leverage to solve an associated problem we call matrix-dictionary recovery.

Improved Active Learning via Dependent Leverage Score Sampling

We show how to obtain improved active learning methods in the agnostic (adversarial noise) setting by combining marginal leverage score sampling with non-independent sampling strategies that promote spatial coverage. In particular, we propose an easily implemented method based on the pivotal sampling algorithm, which we test on problems motivated by learning-based methods for parametric PDEs and uncertainty quantification. In comparison to independent sampling, our method reduces the number of samples needed to reach a given target accuracy by up to $50\%$. We support our findings with two theoretical results. First, we show that any non-independent leverage score sampling method that obeys a weak one-sided $\ell_{\infty}$ independence condition (which includes pivotal sampling) can actively learn $d$ dimensional linear functions with $O(d\log d)$ samples, matching independent sampling. This result extends recent work on matrix Chernoff bounds under $\ell_{\infty}$ independence, and may be of interest for analyzing other sampling strategies beyond pivotal sampling. Second, we show that, for the important case of polynomial regression, our pivotal method obtains an improved bound of $O(d)$ samples.

Moments, Random Walks, and Limits for Spectrum Approximation

We study lower bounds for the problem of approximating a one dimensional distribution given (noisy) measurements of its moments. We show that there are distributions on $[-1,1]$ that cannot be approximated to accuracy $\epsilon$ in Wasserstein-1 distance even if we know \emph{all} of their moments to multiplicative accuracy $(1\pm2^{-\Omega(1/\epsilon)})$; this result matches an upper bound of Kong and Valiant [Annals of Statistics, 2017]. To obtain our result, we provide a hard instance involving distributions induced by the eigenvalue spectra of carefully constructed graph adjacency matrices. Efficiently approximating such spectra in Wasserstein-1 distance is a well-studied algorithmic problem, and a recent result of Cohen-Steiner et al. [KDD 2018] gives a method based on accurately approximating spectral moments using $2^{O(1/\epsilon)}$ random walks initiated at uniformly random nodes in the graph. As a strengthening of our main result, we show that improving the dependence on $1/\epsilon$ in this result would require a new algorithmic approach. Specifically, no algorithm can compute an $\epsilon$-accurate approximation to the spectrum of a normalized graph adjacency matrix with constant probability, even when given the transcript of $2^{\Omega(1/\epsilon)}$ random walks of length $2^{\Omega(1/\epsilon)}$ started at random nodes.

Dimensionality Reduction for General KDE Mode Finding

Finding the mode of a high dimensional probability distribution $D$ is a fundamental algorithmic problem in statistics and data analysis. There has been particular interest in efficient methods for solving the problem when $D$ is represented as a mixture model or kernel density estimate, although few algorithmic results with worst-case approximation and runtime guarantees are known. In this work, we significantly generalize a result of (LeeLiMusco:2021) on mode approximation for Gaussian mixture models. We develop randomized dimensionality reduction methods for mixtures involving a broader class of kernels, including the popular logistic, sigmoid, and generalized Gaussian kernels. As in Lee et al.'s work, our dimensionality reduction results yield quasi-polynomial algorithms for mode finding with multiplicative accuracy $(1-\epsilon)$ for any $\epsilon > 0$. Moreover, when combined with gradient descent, they yield efficient practical heuristics for the problem. In addition to our positive results, we prove a hardness result for box kernels, showing that there is no polynomial time algorithm for finding the mode of a kernel density estimate, unless $\mathit{P} = \mathit{NP}$. Obtaining similar hardness results for kernels used in practice (like Gaussian or logistic kernels) is an interesting future direction.

Active Learning for Single Neuron Models with Lipschitz Non-Linearities

We consider the problem of active learning for single neuron models, also sometimes called ``ridge functions'', in the agnostic setting (under adversarial label noise). Such models have been shown to be broadly effective in modeling physical phenomena, and for constructing surrogate data-driven models for partial differential equations. Surprisingly, we show that for a single neuron model with any Lipschitz non-linearity (such as the ReLU, sigmoid, absolute value, low-degree polynomial, among others), strong provable approximation guarantees can be obtained using a well-known active learning strategy for fitting \emph{linear functions} in the agnostic setting. % -- i.e. for the case when there is no non-linearity. Namely, we can collect samples via statistical \emph{leverage score sampling}, which has been shown to be near-optimal in other active learning scenarios. We support our theoretical results with empirical simulations showing that our proposed active learning strategy based on leverage score sampling outperforms (ordinary) uniform sampling when fitting single neuron models.

Active Sampling for Linear Regression Beyond the $\ell_2$ Norm

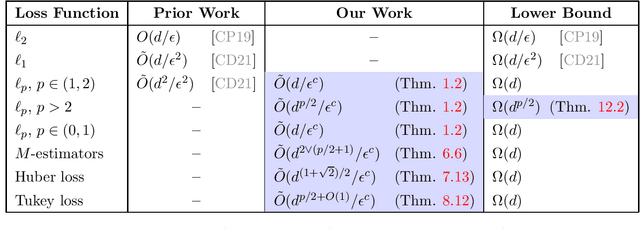
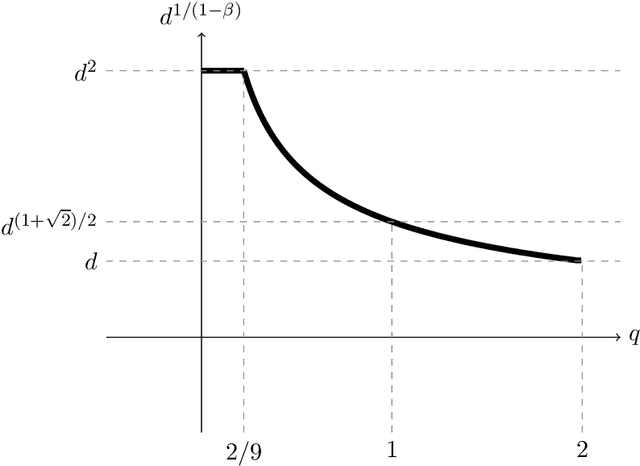
We study active sampling algorithms for linear regression, which aim to query only a small number of entries of a target vector $b\in\mathbb{R}^n$ and output a near minimizer to $\min_{x\in\mathbb{R}^d}\|Ax-b\|$, where $A\in\mathbb{R}^{n \times d}$ is a design matrix and $\|\cdot\|$ is some loss function. For $\ell_p$ norm regression for any $0<p<\infty$, we give an algorithm based on Lewis weight sampling that outputs a $(1+\epsilon)$ approximate solution using just $\tilde{O}(d^{\max(1,{p/2})}/\mathrm{poly}(\epsilon))$ queries to $b$. We show that this dependence on $d$ is optimal, up to logarithmic factors. Our result resolves a recent open question of Chen and Derezi\'{n}ski, who gave near optimal bounds for the $\ell_1$ norm, and suboptimal bounds for $\ell_p$ regression with $p\in(1,2)$. We also provide the first total sensitivity upper bound of $O(d^{\max\{1,p/2\}}\log^2 n)$ for loss functions with at most degree $p$ polynomial growth. This improves a recent result of Tukan, Maalouf, and Feldman. By combining this with our techniques for the $\ell_p$ regression result, we obtain an active regression algorithm making $\tilde O(d^{1+\max\{1,p/2\}}/\mathrm{poly}(\epsilon))$ queries, answering another open question of Chen and Derezi\'{n}ski. For the important special case of the Huber loss, we further improve our bound to an active sample complexity of $\tilde O(d^{(1+\sqrt2)/2}/\epsilon^c)$ and a non-active sample complexity of $\tilde O(d^{4-2\sqrt 2}/\epsilon^c)$, improving a previous $d^4$ bound for Huber regression due to Clarkson and Woodruff. Our sensitivity bounds have further implications, improving a variety of previous results using sensitivity sampling, including Orlicz norm subspace embeddings and robust subspace approximation. Finally, our active sampling results give the first sublinear time algorithms for Kronecker product regression under every $\ell_p$ norm.

Correlation Sketches for Approximate Join-Correlation Queries

The increasing availability of structured datasets, from Web tables and open-data portals to enterprise data, opens up opportunities~to enrich analytics and improve machine learning models through relational data augmentation. In this paper, we introduce a new class of data augmentation queries: join-correlation queries. Given a column $Q$ and a join column $K_Q$ from a query table $\mathcal{T}_Q$, retrieve tables $\mathcal{T}_X$ in a dataset collection such that $\mathcal{T}_X$ is joinable with $\mathcal{T}_Q$ on $K_Q$ and there is a column $C \in \mathcal{T}_X$ such that $Q$ is correlated with $C$. A na\"ive approach to evaluate these queries, which first finds joinable tables and then explicitly joins and computes correlations between $Q$ and all columns of the discovered tables, is prohibitively expensive. To efficiently support correlated column discovery, we 1) propose a sketching method that enables the construction of an index for a large number of tables and that provides accurate estimates for join-correlation queries, and 2) explore different scoring strategies that effectively rank the query results based on how well the columns are correlated with the query. We carry out a detailed experimental evaluation, using both synthetic and real data, which shows that our sketches attain high accuracy and the scoring strategies lead to high-quality rankings.