Agnostic Active Learning of Single Index Models with Linear Sample Complexity

We study active learning methods for single index models of the form $F({\mathbf x}) = f(\langle {\mathbf w}, {\mathbf x}\rangle)$, where $f:\mathbb{R} \to \mathbb{R}$ and ${\mathbf x,\mathbf w} \in \mathbb{R}^d$. In addition to their theoretical interest as simple examples of non-linear neural networks, single index models have received significant recent attention due to applications in scientific machine learning like surrogate modeling for partial differential equations (PDEs). Such applications require sample-efficient active learning methods that are robust to adversarial noise. I.e., that work even in the challenging agnostic learning setting. We provide two main results on agnostic active learning of single index models. First, when $f$ is known and Lipschitz, we show that $\tilde{O}(d)$ samples collected via {statistical leverage score sampling} are sufficient to learn a near-optimal single index model. Leverage score sampling is simple to implement, efficient, and already widely used for actively learning linear models. Our result requires no assumptions on the data distribution, is optimal up to log factors, and improves quadratically on a recent ${O}(d^{2})$ bound of \cite{gajjar2023active}. Second, we show that $\tilde{O}(d)$ samples suffice even in the more difficult setting when $f$ is \emph{unknown}. Our results leverage tools from high dimensional probability, including Dudley's inequality and dual Sudakov minoration, as well as a novel, distribution-aware discretization of the class of Lipschitz functions.

Active Learning for Single Neuron Models with Lipschitz Non-Linearities

We consider the problem of active learning for single neuron models, also sometimes called ``ridge functions'', in the agnostic setting (under adversarial label noise). Such models have been shown to be broadly effective in modeling physical phenomena, and for constructing surrogate data-driven models for partial differential equations. Surprisingly, we show that for a single neuron model with any Lipschitz non-linearity (such as the ReLU, sigmoid, absolute value, low-degree polynomial, among others), strong provable approximation guarantees can be obtained using a well-known active learning strategy for fitting \emph{linear functions} in the agnostic setting. % -- i.e. for the case when there is no non-linearity. Namely, we can collect samples via statistical \emph{leverage score sampling}, which has been shown to be near-optimal in other active learning scenarios. We support our theoretical results with empirical simulations showing that our proposed active learning strategy based on leverage score sampling outperforms (ordinary) uniform sampling when fitting single neuron models.

Subspace Embeddings Under Nonlinear Transformations

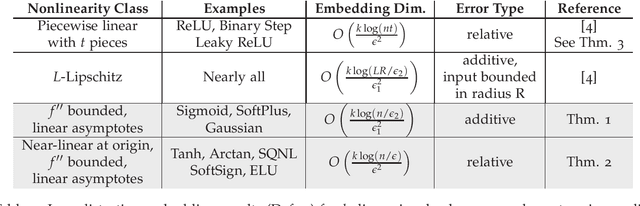
We consider low-distortion embeddings for subspaces under \emph{entrywise nonlinear transformations}. In particular we seek embeddings that preserve the norm of all vectors in a space $S = \{y: y = f(x)\text{ for }x \in Z\}$, where $Z$ is a $k$-dimensional subspace of $\mathbb{R}^n$ and $f(x)$ is a nonlinear activation function applied entrywise to $x$. When $f$ is the identity, and so $S$ is just a $k$-dimensional subspace, it is known that, with high probability, a random embedding into $O(k/\epsilon^2)$ dimensions preserves the norm of all $y \in S$ up to $(1\pm \epsilon)$ relative error. Such embeddings are known as \emph{subspace embeddings}, and have found widespread use in compressed sensing and approximation algorithms. We give the first low-distortion embeddings for a wide class of nonlinear functions $f$. In particular, we give additive $\epsilon$ error embeddings into $O(\frac{k\log (n/\epsilon)}{\epsilon^2})$ dimensions for a class of nonlinearities that includes the popular Sigmoid SoftPlus, and Gaussian functions. We strengthen this result to give relative error embeddings under some further restrictions, which are satisfied e.g., by the Tanh, SoftSign, Exponential Linear Unit, and many other `soft' step functions and rectifying units. Understanding embeddings for subspaces under nonlinear transformations is a key step towards extending random sketching and compressing sensing techniques for linear problems to nonlinear ones. We discuss example applications of our results to improved bounds for compressed sensing via generative neural networks.